正矢

正矢
性質
奇偶性	偶
定義域	(-∞,∞)
到達域	[0,2]
周期	$2\pi$ （360°）
特定值
當x=0	0
當x=+∞	N/A
當x=-∞	N/A
最大值	($(2k+1)\pi$, 2) (360°k+180°, 2)
最小值	($2k\pi$, 0) (360°k, 0)
其他性質
漸近線	N/A
根	$2k\pi$ （$360^{\circ }k$）
臨界點	$k\pi$ （$180^{\circ }k$）
拐點	$k\pi -{\tfrac {\pi }{2}}$ （$180^{\circ }k-90^{\circ }$）
不動點	0
k是一個整數。

單位圓上兩種正矢函數（versin和vercos）和兩種餘矢函數（coversin和covercos）的位置

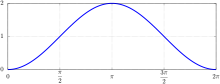
正矢（英文：versine、versed sine）是一種三角函數，出現於早期的三角函數表（如梵語的阿耶巴塔三角表第一節），其值為1和餘弦函數的差${\textrm {versin}}\theta =1-\cos \theta \,$。它的定義域是整個實數集，值域在0到2之間。它是周期函數，其最小正周期為$2\pi$（360°）。在自變量為$(2n+1)\pi$（$360^{\circ }n+180^{\circ }$，其中$n$為整數）時，該函數有極大值2；在自變量為$2n\pi$（或$360^{\circ }n$）時，該函數有極小值0。正矢函數是偶函數，其圖像關於y軸對稱。

概述

正矢函數（versine或versed sine） 是一個三角函數，常計為versin(θ)、 sinver(θ)、 vers(θ)、 ver(θ)或 siv(θ)。 在拉丁語中，其被稱為sinus versus（翻轉的正弦）、 versinus、 versus或 sagitta（箭頭）。

其等價定義為：

$\operatorname {versin} (\theta )=1-\cos(\theta )=2\sin ^{2}\left({\frac {\theta }{2}}\right)$

相關函數

• 餘的正矢（英文：versed cosine、vercosine），寫為vercosin(θ)、 vercos(θ)或 vcs(θ)。

  ${\textrm {vercosin}}(\theta ):=2\cos ^{2}\!\left({\frac {\theta }{2}}\right)=1+\cos(\theta )\,$

• 餘矢（英文：coversed sine、coversine），寫為$\operatorname {coversin} (\theta )$，有時亦縮寫為$\operatorname {cvs} (\theta )$。

  ${\textrm {coversin}}(\theta ):={\textrm {versin}}\!\left({\frac {\pi }{2}}-\theta \right)=1-\sin(\theta )\,$

• 餘的餘矢（英文：coversed cosine或 covercosine），寫為covercosin(θ)、 covercos(θ)或 cvc(θ)。

  ${\textrm {covercosin}}(\theta ):={\textrm {vercosin}}\!\left({\frac {\pi }{2}}-\theta \right)=1+\sin(\theta )\,$

與上述四個函數類似，還存在四個「半值」函數：

• 半正矢（英文：haversed sine, haversine或 semiversus），寫為haversin(θ)、 semiversin(θ)、 semiversinus(θ)、 havers(θ)、 hav(θ)、 hvs(θ)、 sem(θ)或 hv(θ)，因半正矢公式出名，且曾用於導航術。

  ${\textrm {haversin}}(\theta ):={\frac {{\textrm {versin}}(\theta )}{2}}=\sin ^{2}\!\left({\frac {\theta }{2}}\right)={\frac {1-\cos(\theta )}{2}}\,$

• 餘的半正矢（英文：haversed cosine或 havercosine），寫為havercosin(θ), havercos(θ), hac(θ)或 hvc(θ)，其可運用在訊號處理和概率統計上，參見餘的半正矢應用一節。

  ${\textrm {havercosin}}(\theta ):={\frac {{\textrm {vercosin}}(\theta )}{2}}\,$

  $=\cos ^{2}\!\left({\frac {\theta }{2}}\right)={\frac {1+\cos(\theta )}{2}}\,$

• 半餘矢（英文：hacoversed sine、hacoversine或 cohaversine），寫為hacoversin(θ)、 semicoversin(θ)、 hacovers(θ)、 hacov(θ)或 hcv(θ)。

  ${\textrm {hacoversin}}(\theta ):={\frac {{\textrm {coversin}}(\theta )}{2}}={\frac {1-\sin(\theta )}{2}}\,$

• 餘的半餘矢（英文：hacoversed cosine、 hacovercosine或 cohavercosine），寫為hacovercosin(θ)、 hacovercos(θ)或 hcc(θ)。

  ${\textrm {hacovercosin}}(\theta ):={\frac {{\textrm {covercosin}}(\theta )}{2}}={\frac {1+\sin(\theta )}{2}}\,$

歷史與應用

正矢和餘矢

角θ的正弦、餘弦和正矢，以半徑為1、中心為O的單位圓表示。該圖也說明了為什麼正矢有時被稱為sagitta（拉丁語中箭頭的意思）。如果把上下角Δ=2θ的弧ADB看成是「弓」，弦AB看成是「弦」，那麼正矢對應的線段CD顯然就是「箭矢」

歷史上的三角函數與正弦和餘弦的比較。在SVG檔案中，懸停或點擊圖片可以強調對應函數

普通的正弦函數在歷史上有時被稱為sinus rectus （「straight sine」，直譯「直正弦」），以與「versed」的正弦函數，即正矢函數（sinus versus）進行對比。如果在原始上下文中檢視函數的定義（單位圓），這些術語的含義就會很明顯：

對於單位圓的垂直弦AB，角θ（代表上下角Δ的一半）的正弦是距離AC（垂直弦的一半）。另一方面，θ的正矢是從垂直弦的中心到圓弧中心的距離CD。因此，cos(θ)（等於線OC的長度）和versin(θ)（等於線CD的長度）總和就是半徑OD（長度為單位長）。以這種方式說明，正弦是垂直的，而正矢是水平的（正矢又稱為sinus versus，其中versus字面意思是「相反、不合適」）； 兩者都是從點C到圓周的距離，僅差在一個是垂直（正弦），一個是水平（正矢）。

這張圖也說明了為什麼正矢有時被稱為sagitta（拉丁語中箭頭的意思），源自阿拉伯語用法sahem‎，具有相同的含義。 它本身來自印度單字「sara」（箭頭），通常用來指「utkrama-jya」。 如果把上下角Δ=2θ的弧ADB看成是「弓」，弦AB看成是「弦」，那麼正矢對應的線段CD顯然就是「箭矢」。

為了進一步與將正弦解釋為「垂直」並且將正矢解釋為「水平」保持一致，「矢」一字（sagitta）在此也可以視為橫座標（圖中的水平軸）的過時同義詞。

1821年，奧古斯丁-路易·柯西使用術語「sinus versus」（siv）表達正矢，以及使用「cosinus versus」（cosiv）表達餘矢（不過部分文獻混淆了「餘的正矢」與「餘矢」，柯西在1821年的文獻中並未討論到「餘的正矢」，因此它們可能起源於較晚的時間）。

角θ的所有三角函數在幾何上可以依據以O點為圓心的單位圓來構造。

從歷史上看，正矢函數被認為是十分重要的三角函數之一。

當角θ十分接近於0的時候，正矢versin(θ)的值會是兩個幾乎相等的值的差，因此僅使用餘弦函數的三角函數表來計算的話，該表需要非常高的精度才能在避免災難性抵消對於計算正矢函數時所造成的數值誤差，因此製作專用於正矢函數的三角函數表是有必要的。即使是使用計數機或計算機，由於捨入誤差，對於較小的θ，也會建議使用sin²公式來計算正矢值。

正矢的另一個歷史優勢是它的函數值總是非負的，因此除了單一特殊的角度（如θ = 0, 2π, …及其同界角）為零之外，正矢函數的對數在任何地方都有定義，因此，乘法有涉及正矢函數的計算可以使用對數表來計算。

事實上，現存最早的正弦（半弦長）值表（與托勒密和其他希臘作家列出的弦函數表相對）是印度的Surya Siddhantha計算得出的，其可追溯到公元前3世紀，這個表是一個紀錄了從0到90°之每3.75°的正弦和正矢數值的表。

正矢是應用半角公式sin²(θ/2) = 1/2versin(θ)的中間步驟，該公式由托勒密導出，用於建立此類數學用表。

半正矢

更多資訊：半正矢 § 歷史

半正矢函數出現於半正矢公式中，其可以據兩點的經度和緯度來確定大圓上兩點之間距離，且在導航術中被廣泛地使用，因此十九和二十世紀初的導航和三角測量書中包含了半正矢值表和對數表。1835年，詹姆斯·英曼在其著作《航海與航海天文學：供英國海員使用》（Navigation and Nautical Astronomy: For the Use of British Seamen）第三版中創造了「半正矢」一詞以簡化地球表面兩點之間的距離計算，應用於球面三角學關於導航的部分。

現代用途

雖然正矢、餘矢和半正矢及其反函數的使用可以追溯到幾個世紀前，但其他五個餘函數的名稱（餘的正矢、餘的餘矢、半餘矢、餘的半正矢、餘的半餘矢）似乎較晚才出現。

即便如此，這些函數到了近代都還是存在相關應用，例如正矢的相關函數半正矢有應用在一些少見領域的計算方法上，以及餘的半正矢的相關函數則運用於訊號處理、控制理論、概率論和統計學中。

其中正矢的半值函數——半正矢函數在近幾十年來發現了新的應用。如1995年來布魯斯·D·斯塔克（Bruce D. Stark）利用高斯對數之清晰的月角距計算方法，以及2014年提出用於視線縮減之更緊湊的方法。

餘的半正矢

餘的半正矢（havercosine）是餘的正矢（vercosine）之半值函數，其定義為：

${\textrm {havercosin}}(\theta ):={\frac {{\textrm {vercosin}}(\theta )}{2}}=\cos ^{2}\!\left({\frac {\theta }{2}}\right)={\frac {1+\cos(\theta )}{2}}\,$

一個週期（0 < θ < 2π）的正弦或更常見的餘的正矢（vercosine）之半值函數（havercosine）波形也常用於訊號處理和控制理論中，作為脈衝或窗函數的形狀（包括漢恩窗、漢恩–泊松窗和圖基窗），因為它平滑地（在值和斜率上連續）從0遞增到1（對於半正矢）再對稱地遞減回0。在這些應用中，它被稱為漢恩函數或升餘弦濾波器。 同樣，餘的正矢（vercosine）之半值函數（havercosine）也用於概率論和統計學的升餘弦分佈。

結語

綜觀下來，正矢函數被認為是十分重要的三角函數之一，圍繞其的餘函數——餘矢函數亦是如此。主要是為了在計數機與計算機發明之前高度仰賴三角函數表來計算的時代，避免出現災難性抵消對於計算正矢函數以及餘矢函數時所造成的數值誤差。後來發現其對應的半值函數——半正矢能運用在導航術上因此被廣泛使用。相應的每個函數都有其餘函數，在這些函數發展的晚期，這些其餘函數——如餘的正矢、餘的餘矢、半餘矢、餘的半正矢、餘的半餘矢才逐漸被拿來討論。但到了計數機與計算機發明之後，這些函數的需求逐漸式微，因此變得較少使用，但在特定領域仍有發揮空間，如餘的半正矢能應用在訊號處理與概率統計上。

數學性質

定義

正矢、餘矢、餘的正矢、餘的餘矢、半正矢、半餘矢、餘的半正矢、餘的半餘矢定義如下：

正矢	${\textrm {versin}}(\theta ):=2\sin ^{2}\!\left({\frac {\theta }{2}}\right)=1-\cos(\theta )\,$
餘矢	${\textrm {coversin}}(\theta ):={\textrm {versin}}\!\left({\frac {\pi }{2}}-\theta \right)=1-\sin(\theta )\,$
餘的正矢	${\textrm {vercosin}}(\theta ):=2\cos ^{2}\!\left({\frac {\theta }{2}}\right)=1+\cos(\theta )\,$
餘的餘矢	${\textrm {covercosin}}(\theta ):={\textrm {vercosin}}\!\left({\frac {\pi }{2}}-\theta \right)=1+\sin(\theta )\,$
半正矢	${\textrm {haversin}}(\theta ):={\frac {{\textrm {versin}}(\theta )}{2}}=\sin ^{2}\!\left({\frac {\theta }{2}}\right)={\frac {1-\cos(\theta )}{2}}\,$
半餘矢	${\textrm {hacoversin}}(\theta ):={\frac {{\textrm {coversin}}(\theta )}{2}}={\frac {1-\sin(\theta )}{2}}\,$
餘的半正矢	${\textrm {havercosin}}(\theta ):={\frac {{\textrm {vercosin}}(\theta )}{2}}=\cos ^{2}\!\left({\frac {\theta }{2}}\right)={\frac {1+\cos(\theta )}{2}}\,$
餘的半餘矢	${\textrm {hacovercosin}}(\theta ):={\frac {{\textrm {covercosin}}(\theta )}{2}}={\frac {1+\sin(\theta )}{2}}\,$

圓週旋轉

這些函數具備圓週旋轉性值。例如正矢和餘矢即角度差90度、正矢和餘的正矢角度差180度、正矢和餘的餘矢角度差270度，以此類推。半值函數亦然。

${\begin{aligned}\mathrm {versin} (\theta )&=\mathrm {coversin} \left(\theta +{\frac {\pi }{2}}\right)=\mathrm {vercosin} \left(\theta +\pi \right)=\mathrm {covercosin} \left(\theta +{\frac {3\pi }{2}}\right)\\\mathrm {haversin} (\theta )&=\mathrm {hacoversin} \left(\theta +{\frac {\pi }{2}}\right)=\mathrm {havercosin} \left(\theta +\pi \right)=\mathrm {hacovercosin} \left(\theta +{\frac {3\pi }{2}}\right)\end{aligned}}$

微分與積分

${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {versin} (x)=\sin {x}$	$\int \mathrm {versin} (x)\,\mathrm {d} x=x-\sin {x}+C$
${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {vercosin} (x)=-\sin {x}$	$\int \mathrm {vercosin} (x)\,\mathrm {d} x=x+\sin {x}+C$
${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {coversin} (x)=-\cos {x}$	$\int \mathrm {coversin} (x)\,\mathrm {d} x=x+\cos {x}+C$
${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {covercosin} (x)=\cos {x}$	$\int \mathrm {covercosin} (x)\,\mathrm {d} x=x-\cos {x}+C$
${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {haversin} (x)={\frac {\sin {x}}{2}}$	$\int \mathrm {haversin} (x)\,\mathrm {d} x={\frac {x-\sin {x}}{2}}+C$
${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {havercosin} (x)={\frac {-\sin {x}}{2}}$	$\int \mathrm {havercosin} (x)\,\mathrm {d} x={\frac {x+\sin {x}}{2}}+C$
${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {hacoversin} (x)={\frac {-\cos {x}}{2}}$	$\int \mathrm {hacoversin} (x)\,\mathrm {d} x={\frac {x+\cos {x}}{2}}+C$
${\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {hacovercosin} (x)={\frac {\cos {x}}{2}}$	$\int \mathrm {hacovercosin} (x)\,\mathrm {d} x={\frac {x-\cos {x}}{2}}+C$

反函數

這些函數也存在對應的反函數：

• 反正矢（arcversine）：正矢的反函數，又可以記作arcversin、 arcvers、 avers或aver。
• 反餘的正矢（arcvercosine）：餘的正矢的反函數，又可以記作arcvercosin、 arcvercos、 avercos或avcs。
• 反餘矢（arccoversine）：餘矢的反函數，又可以記作arccoversin、 arccovers、 acovers或acvs。
• 反餘的餘矢（arccovercosine）：餘的餘矢的反函數，又可以記作arccovercosin、 arccovercos、 acovercos或acvc。
• 反半正矢（archaversine）：半正矢的反函數，又可以記作archaversin、 archav 、 haversin⁻¹、 invhav、 ahav、 ahvs、 ahv或hav⁻¹。
• 反餘的半正矢（archavercosine）：餘的半正矢的反函數，又可以記作archavercosin、 archavercos或ahvc。
• 反半餘矢（archacoversine）：半餘矢的反函數，又可以記作archacoversin或ahcv。
• 反餘的半餘矢（archacovercosine）：餘的半餘矢的反函數，又可以記作archacovercosin、 archacovercos或ahcc。

$\operatorname {arcversin} (y)=\arccos \left(1-y\right)\,$

$\operatorname {arcvercos} (y)=\arccos \left(y-1\right)\,$

$\operatorname {arccoversin} (y)=\arcsin \left(1-y\right)\,$

$\operatorname {arccovercos} (y)=\arcsin \left(y-1\right)\,$

$\operatorname {archaversin} (y)=2\arcsin \left({\sqrt {y}}\right)=\arccos \left(1-2y\right)\,$

$\operatorname {archavercos} (y)=2\arccos \left({\sqrt {y}}\right)=\arccos \left(2y-1\right)$

$\operatorname {archacoversin} (y)=\arcsin \left(1-2y\right)\,$

$\operatorname {archacovercos} (y)=\arcsin \left(2y-1\right)\,$

其他性質

這些函數皆可以擴展到複平面。

馬克勞林級數：

${\begin{aligned}\operatorname {versin} (z)&=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}z^{2k}}{(2k)!}}\\\operatorname {haversin} (z)&=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}z^{2k}}{2(2k)!}}\end{aligned}}$

$\lim _{\theta \to 0}{\frac {\operatorname {versin} (\theta )}{\theta }}=0$

${\begin{aligned}{\frac {\operatorname {versin} (\theta )+\operatorname {coversin} (\theta )}{\operatorname {versin} (\theta )-\operatorname {coversin} (\theta )}}-{\frac {\operatorname {exsec} (\theta )+\operatorname {excsc} (\theta )}{\operatorname {exsec} (\theta )-\operatorname {excsc} (\theta )}}&={\frac {2\operatorname {versin} (\theta )\operatorname {coversin} (\theta )}{\operatorname {versin} (\theta )-\operatorname {coversin} (\theta )}}\\[3pt][\operatorname {versin} (\theta )+\operatorname {exsec} (\theta )]\,[\operatorname {coversin} (\theta )+\operatorname {excsc} (\theta )]&=\sin(\theta )\cos(\theta )\end{aligned}}$

近似值

對於角度範圍從0到2π的正矢函數與正矢函數的三個近似值的比較

對於角度範圍從0到π/2的正矢函數與正矢函數的三個近似值的比較

當v的正矢函數值versine v與半徑r相比較小時，可以透過以下公式從半弦長度L（上圖所示的AC長）近似得出正矢值： $$v\approx {\frac {L^{2}}{2r}}.$$

或者，如果正矢函數值很小，且已知正矢函數值、半徑和半弦長，則可以透過以下公式來估計計弧長s（上圖所示的AD）： $$s\approx L+{\frac {v^{2}}{r}}$$

這個公式為中國數學家沈括所知，兩個世紀後，郭守敬提出了一個更準確的公式，也涉及弦弧間最大的距離。

工程中使用的更準確的近似是： $$v\approx {\frac {s^{\frac {3}{2}}L^{\frac {1}{2}}}{8r}}$$

任意曲線和弦

術語「正矢」（versine）有時也用來描述任意平面曲線中弦與曲線間最大的距離，上面的圓是其中的一個特例。 給定曲線中兩點之間的弦，從弦到曲線（通常在弦中點）的垂直距離v稱為正矢測量（versine measurement）或軌道曲線正矢測量。對於直線，任何弦的正矢為零，因此該測量表徵了曲線的直線度。在極限情況下，當弦長L趨近於零時，瞬時曲率的比率為8v/L²。 這種用法在鐵路運輸中尤其常見，它描述了鐵軌直線度的測量，並且它是鐵路測量的哈拉德方法之基礎。

其他相關函數

正弦（sin，藍色）、餘弦（cos，洋紅）、全弦（crd，黃色）、正矢（versin，綠色）、和半正矢（haversin，紅色）函數的函數圖形

正矢的值域範圍在0到2之間，類似的函數還有弦函數（crd），值域範圍也在0到2之間，但函數圖形略有差異。正矢函數的圖形與正弦函數的形狀相同，但x軸與y軸都平移了一段距離。正矢函數與其他「正」的三角函數（正弦、正切、正割）同樣是從零開始遞增的函數。

參見

• 三角函數

參考文獻

• Boyer, Carl B. A History of Mathematics 2nd. New York: Wiley. 1991. 
• sagitta. 牛津英語詞典 (第三版). 牛津大學出版社. 2005-09 （英語）. 
• Miller, J. Earliest known uses of some of the words of mathematics (v). [2010-04-02]. （原始內容存檔於2015-09-05）. 
• Calvert, James B. Trigonometry. [2010-04-02]. （原始內容存檔於2007-10-02）. 
• haversine. 牛津英語詞典 (第三版). 牛津大學出版社. 2005-09 （英語）. 
• Cites coinage by Prof. Jas. Inman, D. D., in his Navigation and Nautical Astronomy, 3rd ed. (1835).
• Nair, Bhaskaran. Track measurement systems—concepts and techniques. Rail International. 1972, 3 (3): 159–166. ISSN 0020-8442. 
• 埃里克·韋斯坦因. Haversine. MathWorld. 

外部連結

• Sagitta, Apothem, and Chord （頁面存檔備份，存於互聯網檔案館） by Ed Pegg, Jr., The Wolfram Demonstrations Project.
• 埃里克·韋斯坦因. 正矢. MathWorld.