状态空间 (英语:State-space_representation ),是控制工程 中的一个名词。状态 是指在系统 中可决定系统状态、最小数目变量的有序 集合 [ 1] [ 2]
状态空间表示法即为一种将物理系统表示为一组输入、输出及状态的数学模式,而输入、输出及状态之间的关系可用许多一阶微分方程 来描述。
为了使数学模式不受输入、输出及状态的个数所影响,输入、输出及状态都会以向量 的形式表示,而微分方程(若是线性非时变系统,可将微分方程转变为代数方程)则会以矩阵的形式来表示。
状态空间表示法提供一种方便简捷的方法来针对多输入、多输出的系统进行分析并建立模型。一般频域 的系统处理方式需限制在常系数,启始条件为0的系统。而状态空间表示法对系统的系数及启始条件没有限制。
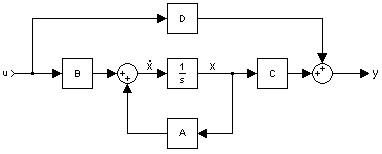
使用状态变数的系统方块图表示 系统的状态变数 是指系统变数中,可以表示任一时间系统完整状态的最小子集合。要表示一系统需要的状态变数最小值n,通常也是该系统微分方程式的阶数。若系统是以传递函数 来表示,状态变数的最小个数等于传递函数分母多项式的阶数。在电路中状态变数的个数常常就是电路中储能元件(如电容器 及电感器 )的个数。
一个有
p
{\displaystyle p}
q
{\displaystyle q}
n
{\displaystyle n}
线性系统 ,可以用以下的状态空间表示法来表示:
x
˙
(
t
)
=
A
(
t
)
x
(
t
)
+
B
(
t
)
u
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}
y
(
t
)
=
C
(
t
)
x
(
t
)
+
D
(
t
)
u
(
t
)
{\displaystyle \mathbf {y} (t)=C(t)\mathbf {x} (t)+D(t)\mathbf {u} (t)}
其中:
x
(
⋅
)
{\displaystyle \mathbf {x} (\cdot )}
x
(
t
)
∈
R
n
{\displaystyle \mathbf {x} (t)\in \mathbb {R} ^{n}}
y
(
⋅
)
{\displaystyle \mathbf {y} (\cdot )}
y
(
t
)
∈
R
q
{\displaystyle \mathbf {y} (t)\in \mathbb {R} ^{q}}
u
(
⋅
)
{\displaystyle \mathbf {u} (\cdot )}
u
(
t
)
∈
R
p
{\displaystyle \mathbf {u} (t)\in \mathbb {R} ^{p}}
A
(
⋅
)
{\displaystyle A(\cdot )}
dim
[
A
(
⋅
)
]
=
n
×
n
{\displaystyle \operatorname {dim} [A(\cdot )]=n\times n}
B
(
⋅
)
{\displaystyle B(\cdot )}
dim
[
B
(
⋅
)
]
=
n
×
p
{\displaystyle \operatorname {dim} [B(\cdot )]=n\times p}
C
(
⋅
)
{\displaystyle C(\cdot )}
dim
[
C
(
⋅
)
]
=
q
×
n
{\displaystyle \operatorname {dim} [C(\cdot )]=q\times n}
D
(
⋅
)
{\displaystyle D(\cdot )}
零矩阵 ),
dim
[
D
(
⋅
)
]
=
q
×
p
{\displaystyle \operatorname {dim} [D(\cdot )]=q\times p}
x
˙
(
t
)
:=
d
d
t
x
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t):={\frac {\operatorname {d} }{\operatorname {d} t}}\mathbf {x} (t)}
通式中所有的矩阵均允许随着时间而变化,此时所表示的就是线性时变系统。若表示的是线性非时变系统 ,则通式的矩阵都不会随着时间变化。时间变数
t
{\displaystyle t}
t
∈
R
{\displaystyle t\in \mathbb {R} }
t
∈
Z
{\displaystyle t\in \mathbb {Z} }
k
{\displaystyle k}
混合系统 允许同时使用连续及离散的时域。依不同的假设,状态空间表示法可以是以下的这些形式:
系统形式
状态空间模型
连续非时变系统
x
˙
(
t
)
=
A
x
(
t
)
+
B
u
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A\mathbf {x} (t)+B\mathbf {u} (t)}
y
(
t
)
=
C
x
(
t
)
+
D
u
(
t
)
{\displaystyle \mathbf {y} (t)=C\mathbf {x} (t)+D\mathbf {u} (t)}
连续时变系统
x
˙
(
t
)
=
A
(
t
)
x
(
t
)
+
B
(
t
)
u
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=\mathbf {A} (t)\mathbf {x} (t)+\mathbf {B} (t)\mathbf {u} (t)}
y
(
t
)
=
C
(
t
)
x
(
t
)
+
D
(
t
)
u
(
t
)
{\displaystyle \mathbf {y} (t)=\mathbf {C} (t)\mathbf {x} (t)+\mathbf {D} (t)\mathbf {u} (t)}
离散非时变系统
x
(
k
+
1
)
=
A
x
(
k
)
+
B
u
(
k
)
{\displaystyle \mathbf {x} (k+1)=A\mathbf {x} (k)+B\mathbf {u} (k)}
y
(
k
)
=
C
x
(
k
)
+
D
u
(
k
)
{\displaystyle \mathbf {y} (k)=C\mathbf {x} (k)+D\mathbf {u} (k)}
离散时变系统
x
(
k
+
1
)
=
A
(
k
)
x
(
k
)
+
B
(
k
)
u
(
k
)
{\displaystyle \mathbf {x} (k+1)=\mathbf {A} (k)\mathbf {x} (k)+\mathbf {B} (k)\mathbf {u} (k)}
y
(
k
)
=
C
(
k
)
x
(
k
)
+
D
(
k
)
u
(
k
)
{\displaystyle \mathbf {y} (k)=\mathbf {C} (k)\mathbf {x} (k)+\mathbf {D} (k)\mathbf {u} (k)}
连续非时变系统
s
X
(
s
)
=
A
X
(
s
)
+
B
U
(
s
)
{\displaystyle s\mathbf {X} (s)=A\mathbf {X} (s)+B\mathbf {U} (s)}
Y
(
s
)
=
C
X
(
s
)
+
D
U
(
s
)
{\displaystyle \mathbf {Y} (s)=C\mathbf {X} (s)+D\mathbf {U} (s)}
离散非时变系统
z
X
(
z
)
=
A
X
(
z
)
+
B
U
(
z
)
{\displaystyle z\mathbf {X} (z)=A\mathbf {X} (z)+B\mathbf {U} (z)}
Y
(
z
)
=
C
X
(
z
)
+
D
U
(
z
)
{\displaystyle \mathbf {Y} (z)=C\mathbf {X} (z)+D\mathbf {U} (z)}
连续线性非时变系统 的稳定性及响应特性可以由矩阵A 的特征值 得到,也可以由系统对应的乘积型传递函数 中得到。其型式如下所示:
G
(
s
)
=
k
(
s
−
z
1
)
(
s
−
z
2
)
(
s
−
z
3
)
(
s
−
p
1
)
(
s
−
p
2
)
(
s
−
p
3
)
(
s
−
p
4
)
{\displaystyle {\textbf {G}}(s)=k{\frac {(s-z_{1})(s-z_{2})(s-z_{3})}{(s-p_{1})(s-p_{2})(s-p_{3})(s-p_{4})}}}
传递函数的分母等于
s
I
−
A
{\displaystyle sI-A}
行列式 所得的特征多项式 :
λ
(
s
)
=
|
s
I
−
A
|
{\displaystyle \mathbf {\lambda } (s)=|sI-A|}
其多项式的根即为矩阵A 的特征值 ,也是传递函数的极点 。极点可以用来分析系统是否为指数稳定 、临界稳定 或者根本不稳定。李雅普诺夫稳定性 是另一种不需计算特征值,也可以判断稳定性的方式。
由传递函数的分子
G
(
s
)
{\displaystyle {\textbf {G}}(s)}
最小相位 。
即使系统没有内部稳定性,仍有可能是输入输出稳定 系统。此情形时的不稳定极点和零点相消,为一个可去奇点 。
传递函数 可用来描述线性非时变系统的特性。一个连续时间的线性非时变系统,可以用以下的方式,将其状态空间表示式转换为传递函数:
首先,对下式进行拉氏转换 ,在初始条件为0(
x
(
0
)
=
0
{\displaystyle \mathbf {x} (0)=\mathbf {0} }
x
˙
(
t
)
=
A
x
(
t
)
+
B
u
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A\mathbf {x} (t)+B\mathbf {u} (t)}
可得到
s
X
(
s
)
=
A
X
(
s
)
+
B
U
(
s
)
{\displaystyle s\mathbf {X} (s)=A\mathbf {X} (s)+B\mathbf {U} (s)}
再针对
X
(
s
)
{\displaystyle \mathbf {X} (s)}
(
s
I
−
A
)
X
(
s
)
=
B
U
(
s
)
{\displaystyle (s\mathbf {I} -A)\mathbf {X} (s)=B\mathbf {U} (s)}
X
(
s
)
=
(
s
I
−
A
)
−
1
B
U
(
s
)
{\displaystyle \mathbf {X} (s)=(s\mathbf {I} -A)^{-1}B\mathbf {U} (s)}
可以用此式来替换以下输出方程式中的
X
(
s
)
{\displaystyle \mathbf {X} (s)}
Y
(
s
)
=
C
X
(
s
)
+
D
U
(
s
)
{\displaystyle \mathbf {Y} (s)=C\mathbf {X} (s)+D\mathbf {U} (s)}
结果如下
Y
(
s
)
=
C
(
(
s
I
−
A
)
−
1
B
U
(
s
)
)
+
D
U
(
s
)
{\displaystyle \mathbf {Y} (s)=C((s\mathbf {I} -A)^{-1}B\mathbf {U} (s))+D\mathbf {U} (s)}
传递函数
G
(
s
)
{\displaystyle \mathbf {G} (s)}
G
(
s
)
=
Y
(
s
)
/
U
(
s
)
{\displaystyle \mathbf {G} (s)=\mathbf {Y} (s)/\mathbf {U} (s)}
因此可得到
G
(
s
)
=
C
(
s
I
−
A
)
−
1
B
+
D
{\displaystyle \mathbf {G} (s)=C(s\mathbf {I} -A)^{-1}B+D}
G
(
s
)
{\displaystyle \mathbf {G} (s)}
q
×
p
{\displaystyle q\times p}
若线性非时变系统有多个输入及输出时,其传递函数(也称为传递矩阵)表示每一组输入及输出的关系,传递矩阵的每一个元素都是一组特定输入及输出的传递函数,不过多重输入多重输出(MIMO)的系统多使用状态空间的方式进行分析,较少使用传递函数或传递矩阵。
将一个系统由状态空间表示式转换为传递函数时,系统内部的资讯无法完整的转换,可能系统表示为状态空间表示式中在特定位置时会不稳定,但是用传递函数表示时却是一个稳定的系统。
一系统的状态可控制性 表示对于系统的一组初始状态及一组终止状态,存在一组输入,使得此系统在有限时间内,可以由初始状态转移到终止状态。一个连续线性时不变系统以状态空间表示时,系统当且仅当 在以下秩 的等式成立时才有可控制性
rank
[
B
A
B
A
2
B
.
.
.
A
n
−
1
B
]
=
n
{\displaystyle \operatorname {rank} {\begin{bmatrix}B&AB&A^{2}B&...&A^{n-1}B\end{bmatrix}}=n}
(秩 就是矩阵中线性独立横行的数目)
可观察性 是可以依一系统的输出得知其系统内部的初始状态。一系统的可观察性及可控制性有数学上的对偶关系,可控制性是指可以利用输入将系统由初始状态转换成任意的最终状态,而可观察性是指系统的输出轨迹预测其初始状态。
一个连续时间的线性非时变系统可观察性,当且仅当下式成立:
rank
[
C
C
A
.
.
.
C
A
n
−
1
]
=
n
{\displaystyle \operatorname {rank} {\begin{bmatrix}C\\CA\\...\\CA^{n-1}\end{bmatrix}}=n}
连续时间线性时不变的状态空间模型可以用以下方式推导其传递函数 :
首先,对下式进行拉普拉斯变换
x
˙
(
t
)
=
A
x
(
t
)
+
B
u
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A\mathbf {x} (t)+B\mathbf {u} (t)}
可得
s
X
(
s
)
−
x
(
0
)
=
A
X
(
s
)
+
B
U
(
s
)
.
{\displaystyle s\mathbf {X} (s)-\mathbf {x} (0)=A\mathbf {X} (s)+B\mathbf {U} (s).}
接下来,化简
X
(
s
)
{\displaystyle \mathbf {X} (s)}
(
s
I
−
A
)
X
(
s
)
=
x
(
0
)
+
B
U
(
s
)
,
{\displaystyle (s\mathbf {I} -A)\mathbf {X} (s)=\mathbf {x} (0)+B\mathbf {U} (s),}
因此
X
(
s
)
=
(
s
I
−
A
)
−
1
x
(
0
)
+
(
s
I
−
A
)
−
1
B
U
(
s
)
.
{\displaystyle \mathbf {X} (s)=(s\mathbf {I} -A)^{-1}\mathbf {x} (0)+(s\mathbf {I} -A)^{-1}B\mathbf {U} (s).}
替换以下输出方程中的
X
(
s
)
{\displaystyle \mathbf {X} (s)}
Y
(
s
)
=
C
X
(
s
)
+
D
U
(
s
)
,
{\displaystyle \mathbf {Y} (s)=C\mathbf {X} (s)+D\mathbf {U} (s),}
Y
(
s
)
=
C
(
(
s
I
−
A
)
−
1
x
(
0
)
+
(
s
I
−
A
)
−
1
B
U
(
s
)
)
+
D
U
(
s
)
.
{\displaystyle \mathbf {Y} (s)=C((s\mathbf {I} -A)^{-1}\mathbf {x} (0)+(s\mathbf {I} -A)^{-1}B\mathbf {U} (s))+D\mathbf {U} (s).}
传递函数
G
(
s
)
{\displaystyle \mathbf {G} (s)}
x
(
0
)
=
0
{\displaystyle \mathbf {x} (0)=\mathbf {0} }
G
(
s
)
×
U
(
s
)
=
Y
(
s
)
{\displaystyle \mathbf {G} (s)\times \mathbf {U} (s)=\mathbf {Y} (s)}
比较
Y
(
s
)
{\displaystyle \mathbf {Y} (s)}
G
(
s
)
=
C
(
s
I
−
A
)
−
1
B
+
D
.
{\displaystyle \mathbf {G} (s)=C(s\mathbf {I} -A)^{-1}B+D.}
可以看出
G
(
s
)
{\displaystyle \mathbf {G} (s)}
q
{\displaystyle q}
p
{\displaystyle p}
q
p
{\displaystyle qp}
针对每一个输入,有
q
{\displaystyle q}
罗森布罗克系统矩阵 提供了状态空间表示法和其传递函数 之间的桥梁。
任一个严格真分 的传递函数,可以依以下的方式转换为状态空间的表示法(以下以一个4阶、单一输入及输出的系统为例):
先将传递函数分子分母展开成以下的形式:
G
(
s
)
=
n
1
s
3
+
n
2
s
2
+
n
3
s
+
n
4
s
4
+
d
1
s
3
+
d
2
s
2
+
d
3
s
+
d
4
{\displaystyle {\textbf {G}}(s)={\frac {n_{1}s^{3}+n_{2}s^{2}+n_{3}s+n_{4}}{s^{4}+d_{1}s^{3}+d_{2}s^{2}+d_{3}s+d_{4}}}}
其分子分母的系数可以放进以下的状态空间表示式中:
x
˙
(
t
)
=
[
−
d
1
−
d
2
−
d
3
−
d
4
1
0
0
0
0
1
0
0
0
0
1
0
]
x
(
t
)
+
[
1
0
0
0
]
u
(
t
)
{\displaystyle {\dot {\textbf {x}}}(t)={\begin{bmatrix}-d_{1}&-d_{2}&-d_{3}&-d_{4}\\1&0&0&0\\0&1&0&0\\0&0&1&0\end{bmatrix}}{\textbf {x}}(t)+{\begin{bmatrix}1\\0\\0\\0\\\end{bmatrix}}{\textbf {u}}(t)}
y
(
t
)
=
[
n
1
n
2
n
3
n
4
]
x
(
t
)
{\displaystyle {\textbf {y}}(t)={\begin{bmatrix}n_{1}&n_{2}&n_{3}&n_{4}\end{bmatrix}}{\textbf {x}}(t)}
这种状态空间的实现方式称为“可控制正则型”(controllable canonical form),方便判断系统的可控制性(控制输入经过一连串的积分器后,即可影响每一个状态),因此。
传递函数也可以转换为以下的状态空间表示式:
x
˙
(
t
)
=
[
−
d
1
1
0
0
−
d
2
0
1
0
−
d
3
0
0
1
−
d
4
0
0
0
]
x
(
t
)
+
[
n
1
n
2
n
3
n
4
]
u
(
t
)
{\displaystyle {\dot {\textbf {x}}}(t)={\begin{bmatrix}-d_{1}&1&0&0\\-d_{2}&0&1&0\\-d_{3}&0&0&1\\-d_{4}&0&0&0\end{bmatrix}}{\textbf {x}}(t)+{\begin{bmatrix}n_{1}\\n_{2}\\n_{3}\\n_{4}\end{bmatrix}}{\textbf {u}}(t)}
y
(
t
)
=
[
1
0
0
0
]
x
(
t
)
{\displaystyle {\textbf {y}}(t)={\begin{bmatrix}1&0&0&0\end{bmatrix}}{\textbf {x}}(t)}
这种状态空间的实现方式称为“可观察正则型”(observable canonical form),方便判断系统的可观察性(输出是经过状态变数一连串积分后的输出,因此可经由状态变数影响系统的输出)。
若传递函数只是真分传递函数 ,不满足严格真分的条件,可以将传递函数分为一严格真分数及常数的和,即可转换为状态空间的表示方式
G
(
s
)
=
G
S
P
(
s
)
+
G
(
∞
)
{\displaystyle {\textbf {G}}(s)={\textbf {G}}_{SP}(s)+{\textbf {G}}(\infty )}
利用上一段的作法可以将严格真分传递函数转换为正则型的状态空间表示式。而常数部分可以转换为
y
(
t
)
=
G
(
∞
)
u
(
t
)
{\displaystyle {\textbf {y}}(t)={\textbf {G}}(\infty ){\textbf {u}}(t)}
A 、B 及C 可利用传递函数的严格真分部分求得,而矩阵D 可利用常数部分求得。
例如以下的真分传递函数
G
(
s
)
=
s
2
+
3
s
+
3
s
2
+
2
s
+
1
=
s
+
2
s
2
+
2
s
+
1
+
1
{\displaystyle {\textbf {G}}(s)={\frac {s^{2}+3s+3}{s^{2}+2s+1}}={\frac {s+2}{s^{2}+2s+1}}+1}
其可控制正则型的实现如下
x
˙
(
t
)
=
[
−
2
−
1
1
0
]
x
(
t
)
+
[
1
0
]
u
(
t
)
{\displaystyle {\dot {\textbf {x}}}(t)={\begin{bmatrix}-2&-1\\1&0\\\end{bmatrix}}{\textbf {x}}(t)+{\begin{bmatrix}1\\0\end{bmatrix}}{\textbf {u}}(t)}
y
(
t
)
=
[
1
2
]
x
(
t
)
+
[
1
]
u
(
t
)
{\displaystyle {\textbf {y}}(t)={\begin{bmatrix}1&2\end{bmatrix}}{\textbf {x}}(t)+{\begin{bmatrix}1\end{bmatrix}}{\textbf {u}}(t)}
其输出直接受到输入的影响,原因就是因为传递函数的常数部分。
典型有反馈的状态空间模型 要为系统增加反馈,可以将输出乘以一矩阵K ,当作系统的输入:
u
(
t
)
=
K
y
(
t
)
{\displaystyle \mathbf {u} (t)=K\mathbf {y} (t)}
x
˙
(
t
)
=
A
x
(
t
)
+
B
u
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A\mathbf {x} (t)+B\mathbf {u} (t)}
y
(
t
)
=
C
x
(
t
)
+
D
u
(
t
)
{\displaystyle \mathbf {y} (t)=C\mathbf {x} (t)+D\mathbf {u} (t)}
可改写为以下的形式
x
˙
(
t
)
=
A
x
(
t
)
+
B
K
y
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A\mathbf {x} (t)+BK\mathbf {y} (t)}
y
(
t
)
=
C
x
(
t
)
+
D
K
y
(
t
)
{\displaystyle \mathbf {y} (t)=C\mathbf {x} (t)+DK\mathbf {y} (t)}
求解
y
(
t
)
{\displaystyle \mathbf {y} (t)}
x
˙
(
t
)
=
(
A
+
B
K
(
I
−
D
K
)
−
1
C
)
x
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=\left(A+BK\left(I-DK\right)^{-1}C\right)\mathbf {x} (t)}
y
(
t
)
=
(
I
−
D
K
)
−
1
C
x
(
t
)
{\displaystyle \mathbf {y} (t)=\left(I-DK\right)^{-1}C\mathbf {x} (t)}
此作法的好处是整个系统的特性不止是由矩阵A 的特征值决定,也可以由K 的适当设定及
(
A
+
B
K
(
I
−
D
K
)
−
1
C
)
{\displaystyle \left(A+BK\left(I-DK\right)^{-1}C\right)}
可控制 的,或者矩阵A 的不稳定特征值可以由适当的K 调整为稳定。
有一种常见的简化法是令矩阵D 为零矩阵 ,矩阵C 为单位矩阵 ,因此方程式可以简化为以下的形式:
x
˙
(
t
)
=
(
A
+
B
K
)
x
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=\left(A+BK\right)\mathbf {x} (t)}
y
(
t
)
=
x
(
t
)
{\displaystyle \mathbf {y} (t)=\mathbf {x} (t)}
需进行特征值分解的矩阵缩小为
A
+
B
K
{\displaystyle A+BK}
输出回授及目标值输入 回授信号也可以再加上目标值 输入
r
(
t
)
{\displaystyle r(t)}
u
(
t
)
=
−
K
y
(
t
)
+
r
(
t
)
{\displaystyle \mathbf {u} (t)=-K\mathbf {y} (t)+\mathbf {r} (t)}
x
˙
(
t
)
=
A
x
(
t
)
+
B
u
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A\mathbf {x} (t)+B\mathbf {u} (t)}
y
(
t
)
=
C
x
(
t
)
+
D
u
(
t
)
{\displaystyle \mathbf {y} (t)=C\mathbf {x} (t)+D\mathbf {u} (t)}
变成以下的形式
x
˙
(
t
)
=
A
x
(
t
)
−
B
K
y
(
t
)
+
B
r
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=A\mathbf {x} (t)-BK\mathbf {y} (t)+B\mathbf {r} (t)}
y
(
t
)
=
C
x
(
t
)
−
D
K
y
(
t
)
+
D
r
(
t
)
{\displaystyle \mathbf {y} (t)=C\mathbf {x} (t)-DK\mathbf {y} (t)+D\mathbf {r} (t)}
求解
y
(
t
)
{\displaystyle \mathbf {y} (t)}
x
˙
(
t
)
=
(
A
−
B
K
(
I
+
D
K
)
−
1
C
)
x
(
t
)
+
B
(
I
−
K
(
I
+
D
K
)
−
1
D
)
r
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=\left(A-BK\left(I+DK\right)^{-1}C\right)\mathbf {x} (t)+B\left(I-K\left(I+DK\right)^{-1}D\right)\mathbf {r} (t)}
y
(
t
)
=
(
I
+
D
K
)
−
1
C
x
(
t
)
+
(
I
+
D
K
)
−
1
D
r
(
t
)
{\displaystyle \mathbf {y} (t)=\left(I+DK\right)^{-1}C\mathbf {x} (t)+\left(I+DK\right)^{-1}D\mathbf {r} (t)}
一个常见的简化是令矩阵D 为零矩阵 ,方程式可简化为以下的形式
x
˙
(
t
)
=
(
A
−
B
K
C
)
x
(
t
)
+
B
r
(
t
)
{\displaystyle {\dot {\mathbf {x} }}(t)=\left(A-BKC\right)\mathbf {x} (t)+B\mathbf {r} (t)}
y
(
t
)
=
C
x
(
t
)
{\displaystyle \mathbf {y} (t)=C\mathbf {x} (t)}
以下以物体的一维移动来作为范例。
考虑一物体在一平面上水平移动,物体和墙壁之间有弹簧相连接,依牛顿第二运动定律 ,其受力如下
m
y
¨
(
t
)
=
u
(
t
)
−
k
1
y
˙
(
t
)
−
k
2
y
(
t
)
{\displaystyle m{\ddot {y}}(t)=u(t)-k_{1}{\dot {y}}(t)-k_{2}y(t)}
其中
y
(
t
)
{\displaystyle y(t)}
y
˙
(
t
)
{\displaystyle {\dot {y}}(t)}
y
¨
(
t
)
{\displaystyle {\ddot {y}}(t)}
u
(
t
)
{\displaystyle u(t)}
k
1
{\displaystyle k_{1}}
k
2
{\displaystyle k_{2}}
m
{\displaystyle m}
其状态方程式可以下式表示
[
x
1
˙
(
t
)
x
2
˙
(
t
)
]
=
[
0
1
−
k
2
m
−
k
1
m
]
[
x
1
(
t
)
x
2
(
t
)
]
+
[
0
1
m
]
u
(
t
)
{\displaystyle \left[{\begin{matrix}\mathbf {\dot {x_{1}}} (t)\\\mathbf {\dot {x_{2}}} (t)\end{matrix}}\right]=\left[{\begin{matrix}0&1\\-{\frac {k_{2}}{m}}&-{\frac {k_{1}}{m}}\end{matrix}}\right]\left[{\begin{matrix}\mathbf {x_{1}} (t)\\\mathbf {x_{2}} (t)\end{matrix}}\right]+\left[{\begin{matrix}0\\{\frac {1}{m}}\end{matrix}}\right]\mathbf {u} (t)}
y
(
t
)
=
[
1
0
]
[
x
1
(
t
)
x
2
(
t
)
]
{\displaystyle \mathbf {y} (t)=\left[{\begin{matrix}1&0\end{matrix}}\right]\left[{\begin{matrix}\mathbf {x_{1}} (t)\\\mathbf {x_{2}} (t)\end{matrix}}\right]}
其中
x
1
(
t
)
{\displaystyle x_{1}(t)}
x
2
(
t
)
=
x
1
˙
(
t
)
{\displaystyle x_{2}(t)={\dot {x_{1}}}(t)}
x
2
˙
(
t
)
=
x
1
¨
(
t
)
{\displaystyle {\dot {x_{2}}}(t)={\ddot {x_{1}}}(t)}
输出
y
(
t
)
{\displaystyle \mathbf {y} (t)}
依可控制性 测试,结果为
[
B
A
B
]
=
[
[
0
1
m
]
[
0
1
−
k
2
m
−
k
1
m
]
[
0
1
m
]
]
=
[
0
1
m
1
m
k
1
m
2
]
{\displaystyle \left[{\begin{matrix}B&AB\end{matrix}}\right]=\left[{\begin{matrix}\left[{\begin{matrix}0\\{\frac {1}{m}}\end{matrix}}\right]&\left[{\begin{matrix}0&1\\-{\frac {k_{2}}{m}}&-{\frac {k_{1}}{m}}\end{matrix}}\right]\left[{\begin{matrix}0\\{\frac {1}{m}}\end{matrix}}\right]\end{matrix}}\right]=\left[{\begin{matrix}0&{\frac {1}{m}}\\{\frac {1}{m}}&{\frac {k_{1}}{m^{2}}}\end{matrix}}\right]}
对所有非零的
k
1
{\displaystyle k_{1}}
依可观察性 测试,结果为
[
C
C
A
]
=
[
[
1
0
]
[
1
0
]
[
0
1
−
k
2
m
−
k
1
m
]
]
=
[
1
0
0
1
]
{\displaystyle \left[{\begin{matrix}C\\CA\end{matrix}}\right]=\left[{\begin{matrix}\left[{\begin{matrix}1&0\end{matrix}}\right]\\\left[{\begin{matrix}1&0\end{matrix}}\right]\left[{\begin{matrix}0&1\\-{\frac {k_{2}}{m}}&-{\frac {k_{1}}{m}}\end{matrix}}\right]\end{matrix}}\right]=\left[{\begin{matrix}1&0\\0&1\end{matrix}}\right]}
对所有非零的
k
1
{\displaystyle k_{1}}
因此,此系统具有可控制性及可观察性。
以下将状态空间模型以函数的形式来表示。
x
˙
(
t
)
=
f
(
t
,
x
(
t
)
,
u
(
t
)
)
{\displaystyle \mathbf {\dot {x}} (t)=\mathbf {f} (t,x(t),u(t))}
y
(
t
)
=
h
(
t
,
x
(
t
)
,
u
(
t
)
)
{\displaystyle \mathbf {y} (t)=\mathbf {h} (t,x(t),u(t))}
第一个方程式为状态方程式,第二个方程式为输出方程式。
此表示法可以表示线性系统及非线性系统。若函数
f
(
⋅
,
⋅
,
⋅
)
{\displaystyle f(\cdot ,\cdot ,\cdot )}
若系统没有外力(没有输入项),则以上方程式中的
u
(
t
)
{\displaystyle u(t)}
单摆 即为一个非线性系统的例子。
m
l
θ
¨
(
t
)
=
−
m
g
sin
θ
(
t
)
−
k
l
θ
˙
(
t
)
{\displaystyle ml{\ddot {\theta }}(t)=-mg\sin \theta (t)-kl{\dot {\theta }}(t)}
其中
θ
(
t
)
{\displaystyle \theta (t)}
m
{\displaystyle m}
g
{\displaystyle g}
k
{\displaystyle k}
l
{\displaystyle l}
m
{\displaystyle m}
其状态方程式为
x
1
˙
(
t
)
=
x
2
(
t
)
{\displaystyle {\dot {x_{1}}}(t)=x_{2}(t)}
x
2
˙
(
t
)
=
−
g
l
sin
x
1
(
t
)
−
k
m
x
2
(
t
)
{\displaystyle {\dot {x_{2}}}(t)=-{\frac {g}{l}}\sin {x_{1}}(t)-{\frac {k}{m}}{x_{2}}(t)}
其中
x
1
(
t
)
=
θ
(
t
)
{\displaystyle x_{1}(t)=\theta (t)}
x
2
(
t
)
=
x
1
˙
(
t
)
{\displaystyle x_{2}(t)={\dot {x_{1}}}(t)}
x
2
˙
=
x
1
¨
{\displaystyle {\dot {x_{2}}}={\ddot {x_{1}}}}
其状态方程式可写成以下的形式
x
˙
(
t
)
=
(
x
1
˙
(
t
)
x
2
˙
(
t
)
)
=
f
(
t
,
x
(
t
)
)
=
(
x
2
(
t
)
−
g
l
sin
x
1
(
t
)
−
k
m
x
2
(
t
)
)
.
{\displaystyle {\dot {x}}(t)=\left({\begin{matrix}{\dot {x_{1}}}(t)\\{\dot {x_{2}}}(t)\end{matrix}}\right)=\mathbf {f} (t,x(t))=\left({\begin{matrix}x_{2}(t)\\-{\frac {g}{l}}\sin {x_{1}}(t)-{\frac {k}{m}}{x_{2}}(t)\end{matrix}}\right).}
一系统的机械平衡点 或驻点 为
x
˙
=
0
{\displaystyle {\dot {x}}=0}
(
x
1
x
2
)
=
(
n
π
0
)
{\displaystyle \left({\begin{matrix}x_{1}\\x_{2}\end{matrix}}\right)=\left({\begin{matrix}n\pi \\0\end{matrix}}\right)}
其中n 为整数。
Antsaklis, P.J. and Michel, A.N. 2007. A Linear Systems Primer , Birkhauser. (ISBN 978-0-8176-4434-50)
Chen, Chi-Tsong 1999. Linear System Theory and Design , 3rd. ed., Oxford University Press (ISBN 978-0-19-511777-6 )
Khalil, Hassan K. 2001 Nonlinear Systems , 3rd. ed., Prentice Hall (ISBN 978-0-13-067389-3 )
Nise, Norman S. 2004. Control Systems Engineering , 4th ed., John Wiley & Sons, Inc. (ISBN 978-0-471-44577-7 )
Hinrichsen, Diederich and Pritchard, Anthony J. 2005. Mathematical Systems Theory I, Modelling, State Space Analysis, Stability and Robustness . Springer. (ISBN 978-3-540-44125-0 )
Sontag, Eduardo D. 1999. Mathematical Control Theory: Deterministic Finite Dimensional Systems. Second Edition . Springer. (ISBN 978-0-387-98489-6 ) (available free online (页面存档备份 ,存于互联网档案馆 ))
Friedland, Bernard. 2005. Control System Design: An Introduction to State Space Methods . Dover. (ISBN 978-0-486-44278-5 ).
Zadeh, Lofti A. and Desoer, Charles A. 1979. Linear System Theory , Krieger Pub Co. (ISBN 978-0-88275-809-1 )















![{\displaystyle \operatorname {dim} [A(\cdot )]=n\times n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdb067922e2d625e2d0aaab3b6e54239cdd4f759)

![{\displaystyle \operatorname {dim} [B(\cdot )]=n\times p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e273a2878042f414ada7b454096d2d66125257a6)

![{\displaystyle \operatorname {dim} [C(\cdot )]=q\times n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa4ac576864f9f09ea580fb19bd480fd12a68be)

![{\displaystyle \operatorname {dim} [D(\cdot )]=q\times p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759072ec7232e15a1823aec56b668df529d57dee)













































































![{\displaystyle \left[{\begin{matrix}\mathbf {\dot {x_{1}}} (t)\\\mathbf {\dot {x_{2}}} (t)\end{matrix}}\right]=\left[{\begin{matrix}0&1\\-{\frac {k_{2}}{m}}&-{\frac {k_{1}}{m}}\end{matrix}}\right]\left[{\begin{matrix}\mathbf {x_{1}} (t)\\\mathbf {x_{2}} (t)\end{matrix}}\right]+\left[{\begin{matrix}0\\{\frac {1}{m}}\end{matrix}}\right]\mathbf {u} (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bde243f9d17f91b1d03020e9559e8120fae677f)
![{\displaystyle \mathbf {y} (t)=\left[{\begin{matrix}1&0\end{matrix}}\right]\left[{\begin{matrix}\mathbf {x_{1}} (t)\\\mathbf {x_{2}} (t)\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/089622c024d88e55fb7da811b54574235a1af4a1)



![{\displaystyle \left[{\begin{matrix}B&AB\end{matrix}}\right]=\left[{\begin{matrix}\left[{\begin{matrix}0\\{\frac {1}{m}}\end{matrix}}\right]&\left[{\begin{matrix}0&1\\-{\frac {k_{2}}{m}}&-{\frac {k_{1}}{m}}\end{matrix}}\right]\left[{\begin{matrix}0\\{\frac {1}{m}}\end{matrix}}\right]\end{matrix}}\right]=\left[{\begin{matrix}0&{\frac {1}{m}}\\{\frac {1}{m}}&{\frac {k_{1}}{m^{2}}}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8085052653d9c3f6548abce458f14b47264c544f)
![{\displaystyle \left[{\begin{matrix}C\\CA\end{matrix}}\right]=\left[{\begin{matrix}\left[{\begin{matrix}1&0\end{matrix}}\right]\\\left[{\begin{matrix}1&0\end{matrix}}\right]\left[{\begin{matrix}0&1\\-{\frac {k_{2}}{m}}&-{\frac {k_{1}}{m}}\end{matrix}}\right]\end{matrix}}\right]=\left[{\begin{matrix}1&0\\0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/379549fbd631c3d00cff027b1208378f396a65e0)













