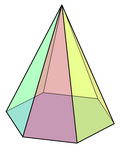
六角錐
外觀
 | ||
| 類別 | 錐體 | |
|---|---|---|
| 對偶多面體 | 六角錐(自身對偶) | |
| 數學表示法 | ||
| 康威表示法 | Y6 | |
| 性質 | ||
| 面 | 7 | |
| 邊 | 12 | |
| 頂點 | 7 | |
| 歐拉特徵數 | F=7, E=12, V=7 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 6個三角形(側面) 1個六邊形(底面) | |
| 頂點圖 | 6(32.6) (36) | |
| 對稱性 | ||
| 對稱群 | C6v, [6], (*66) | |
| 旋轉對稱群 | C6, [6]+, (66) | |
| 特性 | ||
| 凸 | ||
| 圖像 | ||
| ||
在幾何學中,六角錐是指底面為六邊形的錐體,由六邊形各個頂點向它所在的平面外一點依次連直線段而構成。所有六角錐皆為七面體,具有7個面、12個邊和7個頂點,如同其他的錐體,對偶仍為六角錐,是一個自身對偶多面體。
若一個六角錐的底面為正六邊形則可稱為正六角錐,但正六角錐不能算是詹森多面體,因為若每一個面都是正多邊形的話,整個圖形將會共平面,成為六階三角形鑲嵌的一部分。
正六角錐具有C6v對稱性,並且使得其高與底面的交點與任意底面頂點和錐體頂部的頂點可構成直角三角形。
相關多面體與鑲嵌
[編輯]| 正二棱錐 | 正三棱錐 | 正四棱錐 | 正五棱錐 | 正六棱錐 | 正七棱錐 | 正八棱錐 | 正九棱錐 | 正十棱錐 | ... | 圓錐 |
|---|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

|

|
| 球面鑲嵌 | 錐體 | 歐式鑲嵌 仿緊空間 |
雙曲鑲嵌 非緊空間 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 一角錐 C1v, [1] |
 二角錐 C2v, [2] |
 三角錐 C3v, [3] |
 四角錐 C4v, [4] |
 五角錐 C5v, [5] |
 六角錐 C6v, [6] |
 七角錐 C7v, [7] |
 八角錐 C8v, [8] |
 九角錐 C9v, [9] |
 十角錐 C10v, [10] |
... |
 無限角錐 C∞v, [∞] |
 超無限角錐 Ciπ/λv, [iπ/λ] |
參見
[編輯]外部連結
[編輯]- 埃里克·韋斯坦因. Hexagonal Pyramid. MathWorld.
- Virtual Reality Polyhedra(頁面存檔備份,存於網際網路檔案館) www.georgehart.com: The Encyclopedia of Polyhedra
- Conway Notation for Polyhedra(頁面存檔備份,存於網際網路檔案館) Try: "Y6"