一个三角形 余弦定理 是三角形 中三边长度与一个角的余弦 值(
cos
{\displaystyle \cos }
数学式 ,余弦定理指的是:
c
2
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma }
同样,也可以将其改为:
b
2
=
c
2
+
a
2
−
2
c
a
cos
β
{\displaystyle b^{2}=c^{2}+a^{2}-2ca\cos \beta }
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha }
其中
c
{\displaystyle c}
γ
{\displaystyle \gamma }
a
{\displaystyle a}
b
{\displaystyle b}
γ
{\displaystyle \gamma }
勾股定理 则是余弦定理的特殊情况,当
γ
{\displaystyle \gamma }
90
∘
{\displaystyle 90^{\circ }}
cos
γ
=
0
{\displaystyle \cos \gamma =0}
等式 可被简化为
c
2
=
a
2
+
b
2
{\displaystyle c^{2}=a^{2}+b^{2}}
当知道三角形的两边和一角时,余弦定理可被用来计算第三边的长,或是当知道三边的长度时,可用来求出任何一个角。
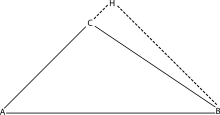
一个钝三角形和它的高。 余弦定理的历史可追溯至公元三世纪前欧几里得 的几何原本 ,在书中将三角形分为钝角和锐角来解释,这同时对应现代数学中余弦值的正负。根据几何原本第二卷的命题12和13[ 1]
A
B
¯
2
=
C
A
¯
2
+
C
B
¯
2
+
2
(
C
A
¯
)
(
C
H
¯
)
{\displaystyle {\overline {AB}}^{2}={\overline {CA}}^{2}+{\overline {CB}}^{2}+2({\overline {CA}})({\overline {CH}})\,}
其中
C
H
¯
=
B
C
¯
cos
(
π
−
γ
)
=
−
B
C
¯
cos
γ
{\displaystyle {\overline {CH}}={\overline {BC}}\cos(\pi -\gamma )=-{\overline {BC}}\cos \gamma }
A
B
¯
2
=
C
A
¯
2
+
C
B
¯
2
−
2
(
C
A
¯
)
(
B
C
¯
)
cos
γ
{\displaystyle {\overline {AB}}^{2}={\overline {CA}}^{2}+{\overline {CB}}^{2}-2({\overline {CA}})({\overline {BC}})\cos \gamma }
具有垂直线的锐角三角形 见右图,在
c
{\displaystyle c}
投影定理 ):
c
=
a
cos
β
+
b
cos
α
{\displaystyle c=a\cos \beta +b\cos \alpha }
将等式同乘以c得到:
c
2
=
a
c
cos
β
+
b
c
cos
α
{\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha }
运用同样的方式可以得到:
a
2
=
a
c
cos
β
+
a
b
cos
γ
{\displaystyle a^{2}=ac\cos \beta +ab\cos \gamma }
b
2
=
b
c
cos
α
+
a
b
cos
γ
{\displaystyle b^{2}=bc\cos \alpha +ab\cos \gamma }
将
c
2
{\displaystyle c^{2}}
c
2
=
a
c
cos
β
+
b
c
cos
α
=
(
a
2
−
a
b
cos
γ
)
+
(
b
2
−
a
b
cos
γ
)
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha =(a^{2}-ab\cos \gamma )+(b^{2}-ab\cos \gamma )=a^{2}+b^{2}-2ab\cos \gamma }
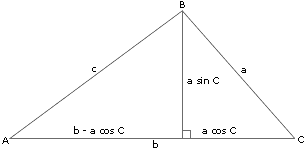
设
△
A
B
C
{\displaystyle \triangle ABC}
A
B
¯
=
c
{\displaystyle {\overline {AB}}=c}
B
C
¯
=
a
{\displaystyle {\overline {BC}}=a}
A
C
¯
=
b
{\displaystyle {\overline {AC}}=b}
B
{\displaystyle B}
A
C
{\displaystyle AC}
垂线 ,垂足为
D
{\displaystyle D}
D
{\displaystyle D}
A
C
{\displaystyle AC}
B
D
{\displaystyle BD}
a
sin
C
{\displaystyle a\sin C}
D
C
{\displaystyle DC}
a
cos
C
{\displaystyle a\cos C}
A
D
{\displaystyle AD}
b
−
a
cos
C
{\displaystyle b-a\cos C}
勾股定理 :
c
2
=
(
a
sin
C
)
2
+
(
b
−
a
cos
C
)
2
{\displaystyle c^{2}=(a\sin C)^{2}+(b-a\cos C)^{2}\,}
c
2
=
a
2
sin
2
C
+
b
2
−
2
a
b
cos
C
+
a
2
cos
2
C
{\displaystyle c^{2}=a^{2}\sin ^{2}C+b^{2}-2ab\cos C+a^{2}\cos ^{2}C\,}
c
2
=
a
2
(
sin
2
C
+
cos
2
C
)
+
b
2
−
2
a
b
cos
C
{\displaystyle c^{2}=a^{2}(\sin ^{2}C+\cos ^{2}C)+b^{2}-2ab\cos C\,}
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C\,}
如果
D
{\displaystyle D}
A
C
{\displaystyle AC}
证明所用的三角形 设
△
A
B
C
{\displaystyle \triangle ABC}
A
B
¯
=
c
{\displaystyle {\overline {AB}}=c}
B
C
¯
=
a
{\displaystyle {\overline {BC}}=a}
A
C
¯
=
b
{\displaystyle {\overline {AC}}=b}
B
{\displaystyle B}
A
C
¯
{\displaystyle {\overline {AC}}}
垂线 ,垂足为
D
{\displaystyle D}
A
D
¯
=
x
{\displaystyle {\overline {AD}}=x}
C
D
¯
=
b
−
x
{\displaystyle {\overline {CD}}=b-x}
勾股定理 :
c
2
−
x
2
=
B
D
¯
2
=
a
2
−
(
b
−
x
)
2
{\displaystyle c^{2}-x^{2}={\overline {BD}}^{2}=a^{2}-(b-x)^{2}}
c
2
−
x
2
=
a
2
−
b
2
−
x
2
+
2
b
x
{\displaystyle c^{2}-x^{2}=a^{2}-b^{2}-x^{2}+2bx}
c
2
=
a
2
−
b
2
+
2
b
x
{\displaystyle c^{2}=a^{2}-b^{2}+2bx}
x
=
b
2
+
c
2
−
a
2
2
b
{\displaystyle x={\frac {b^{2}+c^{2}-a^{2}}{2b}}}
cos
A
=
x
c
=
b
2
+
c
2
−
a
2
2
b
c
{\displaystyle \cos A={\frac {x}{c}}={\frac {b^{2}+c^{2}-a^{2}}{2bc}}}
如果
D
{\displaystyle D}
A
C
¯
{\displaystyle {\overline {AC}}}
余弦定理是解三角形中的一个重要定理。
余弦定理可以简单地变形成:
a
=
b
2
+
c
2
−
2
b
c
cos
A
{\displaystyle a={\sqrt {b^{2}+c^{2}-2bc\cos A}}}
b
=
c
2
+
a
2
−
2
a
c
cos
B
{\displaystyle b={\sqrt {c^{2}+a^{2}-2ac\cos B}}}
c
=
a
2
+
b
2
−
2
a
b
cos
C
{\displaystyle c={\sqrt {a^{2}+b^{2}-2ab\cos C}}}
因此,如果知道了三角形的两边及其夹角,可由余弦定理得出已知角的对边。
余弦定理可以简单地变形成:
cos
A
=
b
2
+
c
2
−
a
2
2
b
c
{\displaystyle \cos A={\frac {b^{2}+c^{2}-a^{2}}{2bc}}\,\!}
cos
B
=
c
2
+
a
2
−
b
2
2
c
a
{\displaystyle \cos B={\frac {c^{2}+a^{2}-b^{2}}{2ca}}\,\!}
cos
C
=
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}\,\!}
因为余弦 函数在
(
0
,
π
)
{\displaystyle ({{\rm {0}},\pi })}
单调性 ,可以得到:
∠
A
=
arccos
b
2
+
c
2
−
a
2
2
b
c
{\displaystyle \angle A=\arccos {\frac {b^{2}+c^{2}-a^{2}}{2bc}}\,\!}
∠
B
=
arccos
c
2
+
a
2
−
b
2
2
c
a
{\displaystyle \angle B=\arccos {\frac {c^{2}+a^{2}-b^{2}}{2ca}}\,\!}
∠
C
=
arccos
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \angle C=\arccos {\frac {a^{2}+b^{2}-c^{2}}{2ab}}\,\!}
因此,如果已知三角形的三边,可以由余弦定理得到三角形的三个内角。
^ In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle. --- Euclid's Elements, translation by Thomas L. Heath.