数学 的分支范畴论 中,单子 (英语:monad ),又称三元组(triple, triad )、标准构造(standard construction )、基本构造(fundamental construction )[ 1] 内函子 范畴 映到自身的函子 ),连同满足特定连贯条件 自然变换 ,三者构成的整体。单子用于研究互为伴随的函子对 ,并将偏序集 上的闭包算子 推广到任意范畴。
单子是一类内函子
F
{\displaystyle F}
G
{\displaystyle G}
伴随函子 ,
F
{\displaystyle F}
G
{\displaystyle G}
G
∘
F
{\displaystyle G\circ F}
F
{\displaystyle F}
G
{\displaystyle G}
恒等函子 。一般而言,伴随关系并不等同范畴的等价 ,而可以联系不同性质的范畴。为了探讨伴随关系所“保持”的性质,数学家研究单子论。理论的另一半,即藉考虑
F
∘
G
{\displaystyle F\circ G}
馀单子 (英语:comonad )。
本条目中,
C
{\displaystyle {\mathcal {C}}}
范畴 。
C
{\displaystyle {\mathcal {C}}}
单子 是函子
T
:
C
→
C
{\displaystyle T:{\mathcal {C}}\to {\mathcal {C}}}
自然变换 ,分别是单位
η
:
1
C
→
T
{\displaystyle \eta :1_{\mathcal {C}}\to T}
1
C
{\displaystyle 1_{\mathcal {C}}}
C
{\displaystyle {\mathcal {C}}}
乘法
μ
:
T
2
→
T
{\displaystyle \mu :T^{2}\to T}
T
2
{\displaystyle T^{2}}
T
∘
T
{\displaystyle T\circ T}
C
{\displaystyle {\mathcal {C}}}
C
{\displaystyle {\mathcal {C}}}
连贯条件
μ
∘
T
μ
=
μ
∘
μ
T
{\displaystyle \mu \circ T\mu =\mu \circ \mu T}
T
3
→
T
{\displaystyle T^{3}\to T}
T
μ
{\displaystyle T\mu }
μ
T
{\displaystyle \mu T}
水平复合 而得。
μ
∘
T
η
=
μ
∘
η
T
=
1
T
{\displaystyle \mu \circ T\eta =\mu \circ \eta T=1_{T}}
T
→
T
{\displaystyle T\to T}
1
T
{\displaystyle 1_{T}}
T
{\displaystyle T}
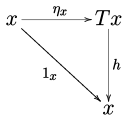
以上两式,亦可以下列交换图 复述:
记号
T
μ
{\displaystyle T\mu }
μ
T
{\displaystyle \mu T}
自然变换 ,又或考虑以下更具体的写法,不用水平复合记号,并将各函子作用在任意物件
X
{\displaystyle X}
定义中,若将
μ
{\displaystyle \mu }
幺半群 乘法结合律 ,而第二条公理类似单位元 的存在性(由
η
{\displaystyle \eta }
C
{\displaystyle {\mathcal {C}}}
C
{\displaystyle {\mathcal {C}}}
E
n
d
C
{\displaystyle \mathbf {End} _{\mathcal {C}}}
幺半群
C
{\displaystyle C}
幺半结构 来自内函子的复合运算。)如此,单子不仅在形式上具有与幺半群 相似的公理,甚而单子就是幺半群的特例。
幂集单子
P
{\displaystyle {\mathcal {P}}}
集合范畴
S
e
t
{\displaystyle \mathbf {Set} }
T
{\displaystyle T}
幂集 运算,即
T
(
A
)
{\displaystyle T(A)}
A
{\displaystyle A}
幂集 ,而对于函数
f
:
A
→
B
{\displaystyle f:A\to B}
T
(
f
)
{\displaystyle T(f)}
A
{\displaystyle A}
像集 ,即
T
(
f
)
(
A
′
)
=
f
[
A
′
]
{\displaystyle T(f)(A')=f[A']}
A
{\displaystyle A}
η
A
:
A
→
T
(
A
)
{\displaystyle \eta _{A}:A\to T(A)}
a
∈
A
{\displaystyle a\in A}
单元子集
{
a
}
{\displaystyle \{a\}}
μ
A
:
T
(
T
(
A
)
)
→
T
(
A
)
,
{\displaystyle \mu _{A}\colon T(T(A))\to T(A),}
将
A
{\displaystyle A}
并集 。以上是幂集单子的定义。
两个单子的复合,未必为单子。举例,幂集单子
P
{\displaystyle {\mathcal {P}}}
P
∘
P
{\displaystyle {\mathcal {P}}\circ {\mathcal {P}}}
[ 2]
取上节定义的范畴论对偶 馀单子 (或馀三元组 )的定义。简单复述,范畴
C
{\displaystyle {\mathcal {C}}}
对偶范畴
C
o
p
{\displaystyle C^{\mathrm {op} }}
C
{\displaystyle {\mathcal {C}}}
C
{\displaystyle {\mathcal {C}}}
U
{\displaystyle U}
馀单位 与馀乘法 (英语:counit and comultiplication )两个自然变换,组成的整体,而三者所要满足的公理,是将原定义中所有态射反转方向而得。
单子之于幺半群,如同馀单子之于馀幺半群 。每个集合皆是馀幺半群,且仅有唯一一种方式,所以抽象代数 中,较少考虑馀幺半群。然而,在线性代数 中,向量空间范畴 (配备张量积 )的馀幺半群较为重要,以馀代数 之名为人所知。
单子的概念最早由罗杰·戈德芒 [ 3] standard construction )。实际上,该书用到的是馀单子,用作解决某个层馀调
其后,单子又出现于彼得·胡伯(Peter Huber )对范畴同伦 的研究中。该论文包含由任意一对伴随函子得出单子的证明。[ 4]
1965年,海因里希·克莱斯利 [ 5] 塞缪尔·艾伦伯格 、约翰·柯曼·摩尔 [ 6] 分别独立 证明反向的结论,即每个单子皆可由某对伴随函子产生。后一篇论文中,将单子称为“三元组”。
1963年,威廉·洛维尔 泛代数 的范畴论。1966年,弗雷德·林顿(Fred Linton )将该理论用单子的语言表达。[ 7] 拓扑 方面的考量,事先似乎比洛维尔的理论更难处理,但已成为用范畴论语言阐述泛代数的方法中,较常见的一个。现今常用的英文名称monad 是1971年由桑德斯·麦克兰恩 在《现职数学家用的范畴 单子论 中的同名哲学概念,即某种能生出其他所有事物的实体。
1980年代,欧金尼奥·莫吉 理论计算机科学 中,利用单子,为电脑程式的若干方面建立模型,包括例外处理、边界情况。[ 8] 函数式编程语言 仔细实作此想法,作为一种基本规律,同样称为单子 [ 9]
若有伴随关系
F
:
C
⇄
D
:
G
{\displaystyle F:{\mathcal {C}}\rightleftarrows {\mathcal {D}}:G}
(即
F
{\displaystyle F}
G
{\displaystyle G}
C
{\displaystyle {\mathcal {C}}}
T
=
G
∘
F
,
{\displaystyle T=G\circ F,}
而单位自然变换来自伴随的单位
η
:
id
C
→
G
∘
F
{\displaystyle \eta :\operatorname {id} _{\mathcal {C}}\to G\circ F}
ε
{\displaystyle \varepsilon }
T
2
=
G
∘
F
∘
G
∘
F
→
G
∘
ε
∘
F
G
∘
F
=
T
.
{\displaystyle T^{2}=G\circ F\circ G\circ F\xrightarrow {G\circ \varepsilon \circ F} G\circ F=T.}
反之,给定单子,可以明确找回一对伴随函子,使单子为该对伴随函子的复合。此构造用到下节定义的
T
{\displaystyle T}
C
T
{\displaystyle C^{T}}
[ 10]
给定域
k
{\displaystyle k}
双重对偶单子 (英语:double dualisation monad )源自伴随关系
(
−
)
∗
:
V
e
c
t
k
⇄
V
e
c
t
k
o
p
:
(
−
)
∗
,
{\displaystyle (-)^{*}:\mathbf {Vect} _{k}\rightleftarrows \mathbf {Vect} _{k}^{\mathrm {op} }:(-)^{*},}
其中两个函子
(
−
)
∗
{\displaystyle (-)^{*}}
k
{\displaystyle k}
向量空间
V
{\displaystyle V}
对偶空间
V
∗
:=
Hom
(
V
,
k
)
{\displaystyle V^{*}:=\operatorname {Hom} (V,k)}
V
{\displaystyle V}
双对偶
V
∗
∗
{\displaystyle V^{**}}
Kock (1970) 对此有更广泛的讨论。
偏序集
(
P
,
≤
)
{\displaystyle (P,\leq )}
x
{\displaystyle x}
y
{\displaystyle y}
当且仅当 偏序中
x
≤
y
{\displaystyle x\leq y}
伽罗瓦连接 ,相应的单子是伽罗华连接的闭包算子 。
又举例,设
G
{\displaystyle G}
群范畴
G
r
p
{\displaystyle \mathbf {Grp} }
集合范畴
S
e
t
{\displaystyle \mathbf {Set} }
遗忘函子 ,将群 映至其基集,又设
F
{\displaystyle F}
自由 函子,由
S
e
t
{\displaystyle \mathbf {Set} }
G
r
p
{\displaystyle \mathbf {Grp} }
F
{\displaystyle F}
G
{\displaystyle G}
T
=
G
∘
F
{\displaystyle T=G\circ F}
X
{\displaystyle X}
F
(
X
)
{\displaystyle F(X)}
{
x
,
x
−
1
:
x
∈
X
}
{\displaystyle \{x,x^{-1}:x\in X\}}
字串 的集合。
该单子的单位变换,由包含映射
η
X
:
X
→
T
(
X
)
{\displaystyle \eta _{X}:X\rightarrow T(X)}
给出,该包含映射将
X
{\displaystyle X}
T
(
X
)
{\displaystyle T(X)}
μ
X
:
T
(
T
(
X
)
)
→
T
(
X
)
{\displaystyle \mu _{X}:T(T(X))\rightarrow T(X)}
是串接 或“压平”运算,将若干条字串组成的串,映至该串中所有字串前后连接而成的一条字串。至此描述完单子的两个自然变换 。
前述例子中,自由群可以推广至其他种类的代数结构,即泛代数 意义下的任意一簇
另外,尚有一个单子源自伴随关系。在向量空间范畴
V
e
c
t
{\displaystyle \mathbf {Vect} }
T
{\displaystyle T}
V
{\displaystyle V}
张量代数
T
(
V
)
{\displaystyle T(V)}
V
{\displaystyle V}
张量代数 ,并有乘法自然变换,在
V
{\displaystyle V}
T
(
T
(
V
)
)
→
T
(
V
)
{\displaystyle T(T(V))\to T(V)}
只要满足某些不强的条件,无左伴随的函子也可以产生单子,称为馀密度单子
F
i
n
S
e
t
{\displaystyle \mathbf {FinSet} }
S
e
t
{\displaystyle \mathbf {Set} }
S
e
t
{\displaystyle \mathbf {Set} }
X
{\displaystyle X}
超滤子 的集合
β
X
{\displaystyle \beta X}
Leinster (2013) 。
给定范畴
C
{\displaystyle {\mathcal {C}}}
(
T
,
η
,
μ
)
{\displaystyle (T,\eta ,\mu )}
C
{\displaystyle {\mathcal {C}}}
T
{\displaystyle {\boldsymbol {T}}}
T
{\displaystyle T}
T
{\displaystyle {\boldsymbol {T}}}
(
x
,
h
)
{\displaystyle (x,h)}
C
{\displaystyle {\mathcal {C}}}
x
{\displaystyle x}
h
:
T
x
→
x
{\displaystyle h:Tx\to x}
结构映射 ),使得图
及
皆可交换。
T
{\displaystyle T}
态射
f
:
(
x
,
h
)
→
(
x
′
,
h
′
)
{\displaystyle f:(x,h)\to (x',h')}
C
{\displaystyle {\mathcal {C}}}
f
:
x
→
x
′
{\displaystyle f:x\to x'}
可交换。于是,
T
{\displaystyle T}
艾伦伯格-摩尔范畴 (英语:Eilenberg–Moore category ),记为
C
T
{\displaystyle {\mathcal {C}}^{T}}
若
T
{\displaystyle T}
自由群单子 ,则
T
{\displaystyle T}
X
{\displaystyle X}
X
{\displaystyle X}
F
(
X
)
{\displaystyle F(X)}
X
{\displaystyle X}
求值 ,evaluation ),且该映射要满足结合律 与单位元的公理。换言之,
X
{\displaystyle X}
F
(
X
)
{\displaystyle F(X)}
X
{\displaystyle X}
X
{\displaystyle X}
另一个例子是集合范畴上的分布单子 (英语:distribution monad )
D
{\displaystyle {\mathcal {D}}}
X
{\displaystyle X}
支撑 的概率分布 的集合。该等分布,是函数
f
:
X
→
[
0
,
1
]
{\displaystyle f:X\to [0,1]}
x
∈
X
{\displaystyle x\in X}
1
{\displaystyle 1}
D
(
X
)
=
{
f
:
X
→
[
0
,
1
]
:
#
supp
(
f
)
<
+
∞
,
∑
x
∈
X
f
(
x
)
=
1
}
.
{\displaystyle {\mathcal {D}}(X)=\left\{f:X\to [0,1]:{\begin{matrix}\#{\text{supp}}(f)<+\infty ,\\\sum _{x\in X}f(x)=1\end{matrix}}\right\}.}
可由定义证明,分布单子上的代数,等同于凸集 ,即集合要配备二元运算
+
r
{\displaystyle +_{r}}
r
∈
[
0
,
1
]
{\displaystyle r\in [0,1]}
欧氏空间 中,凸组合
(
x
,
y
)
↦
r
x
+
(
1
−
r
)
y
{\displaystyle (x,y)\mapsto rx+(1-r)y}
[ 11] [ 12]
另一个有用的单子,是交换环
R
{\displaystyle R}
模范畴
M
o
d
R
{\displaystyle \mathbf {Mod} _{R}}
Sym
∙
(
−
)
:
M
o
d
R
→
M
o
d
R
{\displaystyle {\text{Sym}}^{\bullet }(-):\mathbf {Mod} _{R}\to \mathbf {Mod} _{R}}
将
R
{\displaystyle R}
M
{\displaystyle M}
对称张量
Sym
∙
(
M
)
=
⨁
k
=
0
∞
Sym
k
(
M
)
{\displaystyle {\text{Sym}}^{\bullet }(M)=\bigoplus _{k=0}^{\infty }{\text{Sym}}^{k}(M)}
其中
Sym
0
(
M
)
=
R
{\displaystyle {\text{Sym}}^{0}(M)=R}
Sym
∙
(
R
⊕
n
)
≅
R
[
x
1
,
…
,
x
n
]
{\displaystyle {\text{Sym}}^{\bullet }(R^{\oplus n})\cong R[x_{1},\ldots ,x_{n}]}
R
{\displaystyle R}
交换
R
{\displaystyle R}
。类似地,也有反对称张量
Alt
∙
(
−
)
{\displaystyle {\text{Alt}}^{\bullet }(-)}
T
∙
(
−
)
{\displaystyle T^{\bullet }(-)}
R
{\displaystyle R}
R
{\displaystyle R}
Alt
∙
(
R
⊕
n
)
=
R
(
x
1
,
…
,
x
n
)
,
T
∙
(
R
⊕
n
)
=
R
⟨
x
1
,
…
,
x
n
⟩
,
{\displaystyle {\begin{aligned}{\text{Alt}}^{\bullet }(R^{\oplus n})&=R(x_{1},\ldots ,x_{n}),\\{\text{T}}^{\bullet }(R^{\oplus n})&=R\langle x_{1},\ldots ,x_{n}\rangle ,\end{aligned}}}
前者是
R
{\displaystyle R}
n
{\displaystyle n}
n
{\displaystyle n}
对于可交换
S
{\displaystyle \mathbb {S} }
[ 13] :113 对于可交换
S
{\displaystyle \mathbb {S} }
A
{\displaystyle A}
A
{\displaystyle A}
M
o
d
A
{\displaystyle \mathbf {Mod} _{A}}
A
{\displaystyle A}
P
:
M
o
d
A
→
M
o
d
A
{\displaystyle \mathbb {P} :\mathbf {Mod} _{A}\to \mathbf {Mod} _{A}}
P
(
M
)
=
⋁
j
≥
0
M
j
/
Σ
j
,
{\displaystyle \mathbb {P} (M)=\bigvee _{j\geq 0}M^{j}/\Sigma _{j},}
其中
M
j
=
M
∧
A
⋯
∧
A
M
⏟
j
.
{\displaystyle M^{j}=\underbrace {M\wedge _{A}\cdots \wedge _{A}M} _{j}.}
此函子是单子,而由该单子上的代数范畴,可以得到可交换
A
{\displaystyle A}
C
A
{\displaystyle {\mathcal {C}}_{A}}
如前文 所述,任何伴随关系 皆产生单子。反之,每个单子
T
{\displaystyle T}
T
{\displaystyle T}
T
(
−
)
:
C
⇄
C
T
:
F
.
{\displaystyle T(-):{\mathcal {C}}\rightleftarrows {\mathcal {C}}^{T}:F.}
其中,左伴随
T
(
−
)
{\displaystyle T(-)}
C
{\displaystyle {\mathcal {C}}}
x
{\displaystyle x}
T
{\displaystyle T}
T
(
x
)
{\displaystyle T(x)}
F
{\displaystyle F}
T
{\displaystyle T}
(
x
,
h
)
{\displaystyle (x,h)}
h
{\displaystyle h}
x
{\displaystyle x}
A
d
j
(
C
,
T
)
{\displaystyle \mathbf {Adj} ({\mathcal {C}},T)}
(
F
,
G
,
η
,
ε
)
{\displaystyle (F,G,\eta ,\varepsilon )}
(
G
F
,
η
,
G
ε
F
)
=
(
T
,
η
,
μ
)
{\displaystyle (GF,\eta ,G\varepsilon F)=(T,\eta ,\mu )}
C
{\displaystyle {\mathcal {C}}}
C
T
{\displaystyle {\mathcal {C}}^{T}}
A
d
j
(
C
,
T
)
{\displaystyle \mathbf {Adj} ({\mathcal {C}},T)}
克莱斯利范畴
C
T
{\displaystyle {\mathcal {C}}_{T}}
C
T
{\displaystyle {\mathcal {C}}^{T}}
T
{\displaystyle T}
完全子范畴 ,即仅包含形如
T
(
x
)
{\displaystyle T(x)}
T
{\displaystyle T}
x
{\displaystyle x}
C
{\displaystyle {\mathcal {\mathcal {C}}}}
设有伴随关系
(
F
:
C
→
D
,
G
:
D
→
C
,
η
,
ε
)
{\displaystyle (F:{\mathcal {C}}\to {\mathcal {D}},G:{\mathcal {D}}\to {\mathcal {C}},\eta ,\varepsilon )}
T
{\displaystyle T}
G
{\displaystyle G}
D
→
G
~
C
T
→
F
C
,
{\displaystyle {\mathcal {D}}\xrightarrow {\tilde {G}} {\mathcal {C}}^{T}\xrightarrow {F} {\mathcal {C}},}
其中
F
{\displaystyle F}
D
{\displaystyle {\mathcal {D}}}
Y
{\displaystyle Y}
G
(
Y
)
{\displaystyle G(Y)}
T
{\displaystyle T}
G
~
{\displaystyle {\tilde {G}}}
D
{\displaystyle {\mathcal {D}}}
C
T
{\displaystyle C^{T}}
范畴间的等价 ,则形容该伴随关系为单子的 (英语:monadic )。[ 14]
G
:
D
→
C
{\displaystyle G:{\mathcal {D}}\to {\mathcal {C}}}
F
{\displaystyle F}
G
{\displaystyle G}
单子的 。例如,群范畴 与集合范畴 间的自由-遗忘伴随是单子的,因为相应单子
T
{\displaystyle T}
T
{\displaystyle T}
前文 )。一般而言,若有伴随关系
(
F
:
C
→
D
,
G
:
D
→
C
,
η
,
ε
)
{\displaystyle (F:{\mathcal {C}}\to {\mathcal {D}},G:{\mathcal {D}}\to {\mathcal {C}},\eta ,\varepsilon )}
C
{\displaystyle {\mathcal {C}}}
T
{\displaystyle T}
D
{\displaystyle {\mathcal {D}}}
贝克单子性定理 给出伴随关系在何种充要条件下为单子的。定理有以下简化版:
若满足以下三项条件:
G
{\displaystyle G}
保守函子
G
{\displaystyle G}
反映同构 (英语:reflects isomorphisms ),即对
D
{\displaystyle {\mathcal {D}}}
G
{\displaystyle G}
C
{\displaystyle {\mathcal {C}}}
C
{\displaystyle {\mathcal {C}}}
馀等化子
G
{\displaystyle G}
馀等化子 则
G
{\displaystyle G}
例如,由紧 豪斯多夫空间 范畴
C
H
a
u
s
{\displaystyle \mathbf {CHaus} }
集合范畴
S
e
t
{\displaystyle \mathbf {Set} }
任意拓扑空间范畴
T
o
p
{\displaystyle \mathbf {Top} }
S
e
t
{\displaystyle \mathbf {Set} }
同胚 。[ 15] 拓扑斯论 及有关下降 代数几何 课题有用。
馀单子的伴随关系,首先有下列例子:
−
⊗
A
B
:
M
o
d
A
⇄
M
o
d
B
:
F
,
{\displaystyle -\otimes _{A}B:\mathbf {Mod} _{A}\rightleftarrows \mathbf {Mod} _{B}:F,}
其中
A
,
B
{\displaystyle A,B}
交换环 ,左伴随用到的张量积
⊗
A
{\displaystyle \otimes _{A}}
A
→
B
{\displaystyle A\to B}
F
{\displaystyle F}
B
{\displaystyle B}
忠实平坦
A
{\displaystyle A}
descent datum ,即源自伴随关系的馀单子的作用)的
B
{\displaystyle B}
A
{\displaystyle A}
忠实平坦下降
函数式编程 中,会使用单子表达某类(有时有副作用的)顺序式计算,见单子 (函数式编程) 。
范畴论逻辑中,藉闭包算子 、内代数 ,以及两者与S4模态逻辑 、直觉主义逻辑 的关系,能以单子馀单子理论类比模态逻辑 。
亦可定义2-范畴
C
{\displaystyle {\mathcal {C}}}
^ Barr, Michael; Wells, Charles. Toposes, Triples and Theories [拓扑斯、三元组与理论] (PDF) . Grundlehren der mathematischen Wissenschaften 278 (Springer-Verlag). 1985: 82 and 120 [2021-09-17 ] . ISBN 0-387-96115-1存档 (PDF) 于2020-11-25). ^ Klin; Salamanca. Iterated Covariant Powerset is not a Monad [共变幂集叠代后不是单子]. Electronic Notes in Theoretical Computer Science. 2018-12-01, 341 : 261–276. doi:10.1016/j.entcs.2018.11.013 (英语) . ^ Godement, Roger. Topologie Algébrique et Théorie des Faisceaux [代数拓扑与层论]. Actualités Sci. Ind., Publ. Math. Univ. Strasbourg 1252 . Paris: Hermann. 1958: viii+283 pp (法语) . ^ Huber, Peter J. Homotopy theory in general categories [一般范畴的同伦论]. Mathematische Annalen. 1961, 144 (5): 361–385 (英语) . ^ Kleisli, Heinrich. Every standard construction is induced by a pair of adjoint functors [每个标准构造皆由某对伴随函子产生]. Proceedings of the American Mathematical Society. 1965, 16 (3): 544–546 (英语) . ^ Eilenberg, Samuel ; Moore, John Coleman. Adjoint functors and triples [伴随函子与三元组]. Am. J. Math. 1965, 9 : 301–398 (英语) . ^ Linton, Fred E. J. Some aspects of equational theories [等式理论的若干方面]. Proc. Conf. on Categorical Algebra at La Jolla. 1966: 84–95 (英语) . ^ Moggi, Eugenio. Notions on computation on monads [单子上的计算概念] (PDF) . [2021-09-25 ] . (原始内容存档 (PDF) 于2011-03-22) (英语) . ^ Plotkin, Gordon; Power, John. Adequacy for Algebraic Effects [代数效果的适切性]. Proc. FOSSACS 2001. Lecture Notes in Computer Science 2030 . 2001: 1–24. doi:10.1007/3-540-45315-6_1 (英语) . ^ Riehl (2017 ,162)^ Świrszcz, T. Monadic functors and convexity [单子函子与凸性]. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astron. Phys. 1974, 22 : 39–42. MR 0390019 (英语) . ^
Jacobs, Bart. Convexity, Duality and Effects [凸性、对偶、作用]. Calude, C.S.; Sassone, V. (编). Theoretical Computer Science [理论电脑科学]. IFIP Advances in Information and Communication Technology 323 . 2010: 1–19. ISBN 978-3-642-15239-9doi:10.1007/978-3-642-15240-5_1 (英语) .
^ Basterra, M. André–Quillen cohomology of commutative S-algebras [交换S代数的André–Quillen上同调] . Journal of Pure and Applied Algebra. 1999-12-15, 144 (2): 111–143 [2021-09-18 ] . ISSN 0022-4049 doi:10.1016/S0022-4049(98)00051-6 存档 于2022-01-30) (英语) . ^ MacLane (1978) 所用定义中,条件“等价”要再加强为“同构 ^ MacLane (1978 ,§§VI.3, VI.9)
Barr, Michael; Wells, Charles. Category Theory for Computing Science [电脑科学用的范畴论] (PDF) . 1999 [2021-09-24 ] . (原始内容存档 (PDF) 于2021-12-30) (英语) . Kock, Anders. On Double Dualization Monads [论双重对偶单子]. Mathematica Scandinavica. 1970, 27 : 151. doi:10.7146/math.scand.a-10995 (英语) . Leinster, Tom. Codensity and the ultrafilter monad [馀密度与超滤子单子]. Theory and Applications of Categories. 2013, 28 : 332–370. Bibcode:2012arXiv1209.3606L arXiv:1209.3606 (英语) . MacLane, Saunders. Categories for the Working Mathematician [现职数学家用的范畴]. Graduate Texts in Mathematics 5 . 1978. ISBN 978-1-4419-3123-8doi:10.1007/978-1-4757-4721-8 (英语) . Pedicchio, Maria Cristina; Tholen, Walter (编). Categorical Foundations. Special Topics in Order, Topology, Algebra, and Sheaf Theory [范畴基础。序、拓扑、代数、层论特别专题]. Encyclopedia of Mathematics and Its Applications 97 . Cambridge: Cambridge University Press . 2004. ISBN 0-521-83414-7Zbl 1034.18001 (英语) . Riehl, Emily. Category Theory in Context [脉络中的范畴论] (PDF) . 2017. ISBN 9780486820804存档 (PDF) 于5 Apr 2021) (英语) . Turi, Daniele. Category Theory Lecture Notes [范畴论讲义] (PDF) . 1996–2001 [2021-09-24 ] . (原始内容存档 (PDF) 于2022-02-21) (英语) .






 (英语).
(英语).
 (英语).
(英语).
 . (原始内容存档于2022-01-30) (英语).
. (原始内容存档于2022-01-30) (英语).
 (英语).
(英语). (英语).
(英语). (英语).
(英语).






























![{\displaystyle T(f)(A')=f[A']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3f7249d370cf73c7730152c0033cd5929296a46)











































![{\displaystyle f:X\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbce99d737c06662e393d2d3dba7505a1e6c6eb6)


![{\displaystyle {\mathcal {D}}(X)=\left\{f:X\to [0,1]:{\begin{matrix}\#{\text{supp}}(f)<+\infty ,\\\sum _{x\in X}f(x)=1\end{matrix}}\right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26b35016b9010f235d9755c3a45a05113967e21e)

![{\displaystyle r\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d4a8acea9f5c4e59d8f5fd0ea3c695efa7252fe)







![{\displaystyle {\text{Sym}}^{\bullet }(R^{\oplus n})\cong R[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54cf697c5af77176206c0c60aaae8be07d536615)
































