波耳模型

在波耳模型裡，被約束於原子殼層的帶負價電子，繞著帶正價原子核進行圓周運動。從一個軌道躍遷至另一個軌道會伴隨著離散能量以電磁波的形式被發射或吸收。在圖中，電子的軌道顯示為灰色圓圈，其半徑隨著主量子數平方n²增加，從主量子數3 → 2的躍遷製成了巴耳末系的第一條譜線，波長為656 nm （紅光）。

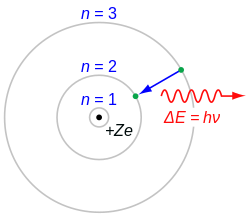
波耳模型是丹麥物理學家尼爾斯·波耳於1913年提出的關於原子結構的模型。此模型引入量子化的概念來研究原子內電子的運動，對於計算氫原子光譜的芮得柏公式給出了理論解釋。波耳模型是20世紀初期物理學取得的重要成就，對原子物理學產生了深遠的影響。

波耳模型的提出

丹麥物理學家尼爾斯·波耳（1885—1962）

20世紀初期，德國物理學家普朗克為解釋黑體輻射現象，提出能量量子化假說，揭開了量子理論的序幕。1885年，瑞士數學教師巴耳末將氫原子的譜線表示成巴耳末公式。然而巴耳末公式是經驗公式，直到波耳在1913年提出波耳模型為止，人們並不了解它們的物理含義。

1911年，英國物理學家拉塞福根據1909年開始進行的α粒子散射實驗，提出了原子的拉塞福模型。在這個模型里，原子的中心有一個帶正電（Ze）、帶質量的原子核，在原子核的四周是帶負電的電子雲；其中，Z是原子數，e是單位電荷。從拉塞福模型，拉塞福推導出散射公式，其預測與實驗結果相符合。然而，在拉塞福散射實驗裡，主角是原子核，而電子並不重要，因此拉塞福不能空口無憑地給出電子的排列方式，也無法用這模型對於化學結合、元素列表、原子譜線給出解釋。

1912年，正在英國曼徹斯特大學工作的波耳將一份被後人稱作《曼徹斯特備忘錄》的草稿提交給他的導師拉塞福。在這份直到波耳過世後才被發布的草稿中，波耳在拉塞福模型的基礎上引入了普朗克的量子概念，波耳提議，原子可以維持力學穩定性，前提是電子的動能$T$與電子環繞原子核的公轉頻率$\nu$，兩者之間的關係式假定為

$T=k\nu$；

其中，$k$與普朗克常數有關。

注意到他並沒有確切給出$k$的形式，也沒有將輻射穩定性納入考量，更沒有理論證實他的假定可以達成力學穩定性。

1913年2月4日前後的某一天，波耳與同事漢斯·漢森討論他的研究，漢森提問：「這研究與譜線方程式有甚麼關係?」波耳回答說他會去查閱這方面的資料。波耳博覽那時期的科學文獻，而且巴耳末公式在科學文獻裡是常被引述的譜線方程式，很可能他已看到過這公式，但並沒有注意到這公式與自己研究有甚麼的關聯，而且已完全忘掉這公式。不論如何，他詳細閱讀了約翰內斯·史塔克撰寫的教科書（德文）有關譜線方面的內容，特別是關於巴耳末公式的描述，後來他回憶：「就在我看到巴耳末公式的那一瞬間，突然一切都變得清楚了。」3月7日，他寫好一篇詮釋巴耳末公式的論文，其開啟了原子結構的量子理論。

1913年7月、9月、11月，《哲學雜誌》接連刊載了波耳的三篇論文，標誌著波耳模型正式提出。這三篇論文成為物理學史上的古典，被稱為波耳模型的「三部曲」。他在第一篇論文中利用波耳模型分析了氫原子，在第二篇論文中論述了其它原子結構與週期表，在第三篇論文中探討了分子結構。

波耳模型的主要內容

波耳模型的兩個主要假設為，

• 在氫原子中，電子圍繞著原子核進行圓周運動。
• 在軌道中運動的電子的角動量的大小 $L$ 被量子化為正整數乘以約化普朗克常數 $\hbar$。

軌道半徑量子化

按照第一個假設，在氫原子中的電子，圍繞著原子核做圓周運動，其軌道是古典軌道。電子做圓周運動的向心力是由電子和原子核之間的庫侖力所提供：

$m_{e}{\frac {v^{2}}{r}}={\frac {1}{4\pi \varepsilon _{0}}}{\frac {e^{2}}{r^{2}}}$，

其中，$m_{e}$ 是電子質量，$v$ 是電子速率，$r$ 是電子軌道半徑，$\varepsilon _{0}$ 是電常數，$e$ 是基本電荷。

所以，半徑為

$r={\frac {1}{4\pi \varepsilon _{0}}}{\frac {e^{2}}{m_{e}v^{2}}}$，

另外，圓周運動的角動量大小是半徑乘以動量：

$L=rm_{e}v$。

所以，按照第二個假設，速度為

$v=L/rm_{e}=n\hbar /rm_{e}$，

其中，$n$ 是主量子數，$\hbar$ 是約化普朗克常數。

將速度的表達式代入半徑的表達式，可以得到新的半徑的表達式

$r={\frac {4\pi \varepsilon _{0}\hbar ^{2}}{m_{e}e^{2}}}n^{2}$。

這軌道半徑表達式可以重寫為

$r=an^{2}$；

其中，$a={\frac {4\pi \varepsilon _{0}\hbar ^{2}}{m_{e}e^{2}}}\approx 5.29\times 10^{-11}m$ 是波耳半徑。

在氫原子的波爾模型裡，以原子核為圓心的電子圓周運動的半徑被量子化，最小的半徑是波耳半徑。由於電子被禁止離原子核更近，庫侖力無法將電子吸引到原子核裡，電子也不會因為進行圓周運動的加速度而釋出電磁波。

軌道能量量子化

電子繞著原子核的軌道能量 $E$ 是動能 $K$ 加位能 $V$ ：

$E=K+V={\frac {1}{2}}m_{e}v^{2}-{\frac {e^{2}}{4\pi \varepsilon _{0}r}}=-{\frac {e^{2}}{8\pi \varepsilon _{0}r}}$。

將軌道半徑表達式代入軌道能量表達式，可以得到

$E=-{\frac {m_{e}e^{4}}{8\varepsilon _{0}^{2}h^{2}}}\ {\frac {1}{n^{2}}}\approx -{\frac {13.60eV}{n^{2}}}$。

在氫原子的波爾模型裡，軌道能量被量子化，並與主量子數的平方成反比。這是束縛電子的能量。由於原子核被假設為固定不動，這能量也可以視為整個氫原子的能量。

躍遷能量變化

電子只能夠穩定地存在於一系列的離散的能量狀態之中，稱為定態。假若電子的能量發生任何變化，都必須要在兩個定態之間以躍遷的方式進行，所以電子只能處於一系列分立的定態。當電子從一個定態躍遷至另一個定態時，會以電磁波的形式放出或吸收能量：

$h\nu =\Delta E=E_{n'}-E_{n}$，

其中，$\nu$ 是電磁波的頻率。

將軌道能量表達式代入這公式，可以得到

${\frac {1}{\lambda }}=-{\frac {m_{e}e^{4}}{8\varepsilon _{0}^{2}h^{3}c}}\left({\frac {1}{n'^{2}}}-{\frac {1}{n^{2}}}\right)$。

將這表達式重寫，可以得到芮得柏公式：

${\frac {1}{\lambda }}=R\left({\frac {1}{n^{2}}}-{\frac {1}{n'^{2}}}\right)$。

其中，$R={\frac {m_{e}e^{4}}{8\varepsilon _{0}^{2}h^{3}c}}$ 是芮得柏常數。

修正

英國光譜學家亞弗列德·福勒質疑：應用波耳模型計算出芮得柏常數的數值$R=109737.315\,\mathrm {cm} ^{-1}$；而實驗值$R=109677.58\,\mathrm {cm} ^{-1}$，二者相差大約萬分之五。1914年，波耳提出，這是因為原來的模型假設原子核靜止不動而引起的。實際情況是，原子核的質量不是無窮大，它與電子繞共同的質心轉動。波耳對其理論進行了修正，用原子核和電子的約化質量$\mu ={\frac {m_{e}M}{m_{e}+M}}$代替了電子質量。這樣的話，不同原子的芮得柏常數R_A不同，

$R_{A}={\frac {R}{1+m_{e}/M}}$

電子到質心的距離仍為原來理論中的第一軌道半徑，與原子核的質量無關。

波耳模型的實驗驗證

1897年，美國天文學家愛德華·皮克林在恆星弧矢增二十二的光譜中發現了一組獨特的線系，稱為皮克林線系。皮克林線系中有一些譜線靠近巴耳末線系，但又不完全重合，另外有一些譜線位於巴耳末線系兩臨近譜線之間。起初皮克林線系被認為是氫的譜線，然而波耳提出皮克林線系是類氫離子He⁺發出的譜線。隨後英國物理學家埃萬斯在實驗室中觀察了He⁺的光譜，證實波耳的判斷完全正確。

和波耳提出波耳模型幾乎同一時期，英國物理學家亨利·莫斯利測定了多種元素的X射線標識譜線，發現它們具有確定的規律性，並得到了經驗公式——莫斯利定律。莫斯利看到波耳的論文，立刻發現這個經驗公式可以由波耳模型導出，為波耳模型提供了有力的證據。

1914年，詹姆斯·法蘭克和古斯塔夫·赫茲進行了用電子轟擊汞蒸汽的實驗，即法蘭克-赫茲實驗。實驗結果顯示，汞原子內確實存在能量為4.9eV的量子態。1920年代，法蘭克和赫茲又繼續改進實驗裝置，發現了汞原子內部更多的量子態，有力地證實了波耳模型的正確性。

1932年，哈羅德·尤里觀察到了氫的同位素氘的光譜，測量到了氘的芮得柏常數，和波耳模型的預言符合得很好。

波耳模型的推廣

隨著光譜實驗水平的提高，人們發現了光譜具有精細結構。1896年，阿爾伯特·邁克生和愛德華·莫雷觀察到了氫光譜的H_α線是雙線，隨後又發現是三線。波耳提出這可能是電子在橢圓軌道上做慢進動引起的。1916年索末菲在波耳模型的基礎上將圓軌道推廣為橢圓形軌道，並且引入相對論修正，提出了索末菲模型。在考慮橢圓軌道和相對論修正後，索末菲計算出了H_α線的精細結構，與實驗相符。然而進一步的研究發現，這樣的解釋純屬巧合。H_α線的精細結構有7條，必須徹底拋棄電子軌道的概念才能完全解釋光譜的精細結構。

波耳模型的問題

波耳模型將古典力學的規律應用於微觀的電子，不可避免地存在一系列問題。根據古典電動力學，做加速運動的電子會輻射出電磁波，致使能量不斷損失，而波耳模型無法解釋為什麼處於定態中的電子不發出電磁輻射。波耳模型對躍遷的過程描寫含糊。因此波耳模型提出後並不被物理學界所歡迎，還遭到了包括拉塞福、薛丁格在內的諸多物理學家的質疑。波耳曾經的導師、劍橋大學的約瑟夫·湯姆森拒絕對其發表評論。薛丁格甚至評價說是「糟透的躍遷」。

此外，波耳模型無法揭示氫原子光譜的強度和精細結構，也無法解釋稍微複雜一些的氦原子的光譜，以及更複雜原子的光譜。因此，波耳在領取1922年諾貝爾物理學獎時稱：「這一理論還是十分初步的，許多基本問題還有待解決。」

波耳模型引入了量子化的條件，但它仍然是一個「半古典半量子」的模型。完全解決原子光譜的問題必須徹底拋棄古典的軌道概念。儘管波耳模型遇到了諸多困難，然而它顯示出量子假說的生命力，為古典物理學向量子物理學發展鋪平了道路。

參閱

• 尼爾斯·波耳
• 芮得柏公式
• 惰性電子對效應可以用波耳模型解釋。
• 原子軌域