User:Yinweichen/Testpage1

  此用户页的主題是相对论中的引力波。关于流體力學中的重力波，請見「重力波 (流體力學)」。

在物理學中，重力波指時空曲率中以波的形式從射源向外傳播的擾動，這種波會以重力輻射的形式傳遞能量。阿爾伯特·愛因斯坦根據他的廣義相對論，於1916年預言了重力波的存在。理論上可以被探測到的重力波射源包括由白矮星、中子星或黑洞組成的聯星系統。重力波現象是廣義相對論的勞倫茲不變性的結果之一，因為它限制了交互作用的傳播速度。相反，牛頓重力理論中的交互作用都以無限的速度傳播，所以在這一理論下並不存在重力波。

科學家已通過各種間接方法發現了重力輻射的證據。例如，拉塞爾·赫爾斯和約瑟夫·泰勒發現赫爾斯－泰勒脈衝雙星在互相公轉時逐漸靠近，這為重力輻射的存在提供了證據；兩人因這項發現於1993年獲得了諾貝爾物理學獎。科學家也利用重力波探測器來觀測重力波現象，如簡稱LIGO的激光干涉重力波天文台。2014年3月17日，哈佛－史密松天體物理中心的天文學家宣佈利用BICEP2探測器在宇宙微波背景中直接觀測到重力波，並且取得了第一幅原始宇宙重力波的直接圖像，這為宇宙暴脹和大爆炸理論提供了強烈的證據。截至2014年3月 (2014-03)，這項研究仍待同行評審。

概述

宇宙的历史。根据推测，大爆炸刚发生后的超光速暴涨过程产生了引力波。

愛因斯坦廣義相對論所描述的重力，是時空曲率所產生的一種現象。質量可以導致這種曲率。當物質在時空中運動時，附近的曲率就會隨之改變。大質量物體運動時所產生的曲率變化會以光速像波一樣向外傳播。這一傳播現象就是重力波。

當重力波通過遠處的觀測者時，觀測者會發現時空被扭曲了。兩個自由物體之間的距離會有節奏地波動，頻率與重力波相同。然而，在這一過程中，這兩個自由物體並沒有受力，座標位置也沒有變化；改變的，是時空座標本身的距離。在觀測者處的重力波強度和與波源間的距離呈反比。根據預測，螺旋形靠近的中子雙星系統由於質量高、加速度高，因此在合併時會發射出強大的重力波。但是因為天文距離尺度之大，就算是最激烈的事件所產生的重力波，在到達地球後效應已變得極低，其應變的數量級低於10⁻²¹分之一。為了探測到這種細微的變化，科學家不斷增加探測器的靈敏度。截至2012年 (2012-Missing required parameter 1=month!)，最為敏感的探測器位於LIGO和VIRGO天文台，靈敏度高達7022499999999999999♠5×10²²分之一。這些天文台未能探測到重力波，這為這種重力波的頻率設下了上限。歐洲空間局正在研發一座用來探測重力波的空間天文台，激光干涉空間天線（LISA） 。

線性偏振重力波

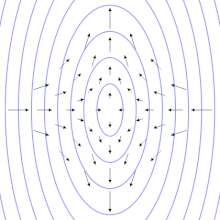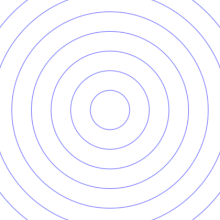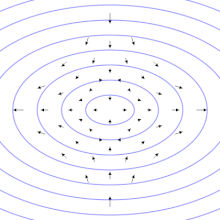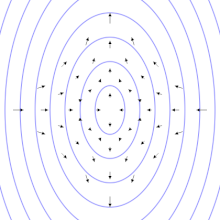
重力波能夠穿透電磁波所無法穿透的空間。科學家推測，重力波能夠幫助了解位於宇宙遠處的各種天體，例如黑洞。這類天體無法用光學望遠鏡和射電望遠鏡等傳統方式觀測。宇宙學家還能夠利用重力波來觀測宇宙最早期狀態。傳統的天文學方法無法用來直接觀測早期宇宙，因為在復合之前，宇宙無法被電磁波所穿透。對重力波更精確的測量還能進一步驗證廣義相對論。

重力波理論上可以取任何頻率，但極低頻率幾乎無法探測，而極高頻率也沒有可觀測的已知波源。史蒂芬·霍金和維爾納·伊斯雷爾（Werner Israel）預測，可以被探測到的重力波頻率在10⁻⁷ Hz和10¹¹ Hz之間。

重力波通過時的效應

一個由粒子組成的環在十字型偏振重力波下的作用

一個由粒子組成的環在交叉型偏振重力波下的作用

要了解重力波通過觀測者時的作用，可以想像一個完全平坦的時空區域，裡面有一組靜止的試驗粒子形成一個平面。當重力波沿著垂直於該平面的方向通過這些粒子的時候，它們就會隨著扭曲了的時空而「十字形」擺動（見右邊動畫）。試驗粒子所包圍之面積不變，而且粒子不會沿波傳播的方向運動。當橫向粒子距離最大時，縱向的粒子距離就最小；相反，橫向離子距離最小時，縱向粒子距離就最大。

動畫大大誇大了粒子的擺動，重力波的振幅實際上是非常小的。兩個質量互相作圓周軌道運動，就可以產生這種效果。在這種情況下，重力波的振幅不變，但其偏振平面會以公轉週期的兩倍旋轉。所以重力波大小（週期性時空應變）會隨時間改變，如動畫所示。如果軌道呈橢圓形，則振幅本身也會隨時間變化。

正如其他波一樣，重力波也有幾項特徵屬性：

• 振幅：通常記作h，描述波大小的一個無量綱量，是兩個粒子間距離的最大擠壓度佔原距離的比例。動畫中的振幅大約為h=0.5。兩個黑洞合併時所產生的重力波在通過地球時，振幅只有h~10⁻²¹。
• 頻率：通常記作f，波振動的頻率（1除以兩次最大擠壓之間的時間間隔）。
• 波長：通常記作λ，波的兩個最大擠壓處之間的空間間隔。
• 速度：波傳播的速度。在廣義相對論中，重力波以光速c傳播。

從這些量可以算出，重力波的光度為一個關於四極矩的三階時間導數的函數。

重力波的速度、波長和頻率之間的關係為c = λ f，這與電磁波的對應方程相同。例如，動畫中的粒子大約每2秒擺動一次，即頻率為0.5 Hz，波長約為600,000 km，即大約地球直徑的47倍。

以上例子假設了波具有「十字型」線性偏振，記作$h_{+}$。和光波的偏振不同的是，重力波的偏振之間呈45度角，而非90度。如果偏振為「交叉型」$h_{\times }$，那麼試驗粒子的波動十分相似，只是方向旋轉了45度，正如第二幅動畫所示。和光波一樣，重力波偏振還可以以圓偏振波表示。重力波的偏振取決於波源的性質和角度。

振幅上限的估算

一个典型系统的四极矩分量$Q_{ij}$具有$MR^{2}$的量级，这里M是系统的质量，R是系统的尺寸半径，因此可以认为这一分量对时间的二阶导数具有$Mv^{2}$的量级，其中$v^{2}$是系统内部引起引力辐射的运动速度的平方。则代入四极矩公式可得辐射的引力波强度为

$h\sim {\frac {2Mv^{2}}{r}}$。

注意到这里${\frac {M}{r}}$就是波源外部距离为r处的牛顿引力势，引力波强度与外部引力势$\phi _{ext}$的比值$\epsilon$为

$\epsilon \sim 2v^{2}$。

根据自引力系统的位力定理，这个比值不能大于波源内部牛顿引力势的最大值$\phi _{int}$。这样得到了一个很方便实用的估算引力波振幅上限的方法：

$h<\phi _{int}\phi _{ext}$。

对于一个在室女座星系团内放出引力辐射的中子星，可估算出其引力辐射的上限为5×10^-22。几十年来，科學家都利用这种方法來估算引力波探测器灵敏度的最低要求。

频率上限的估算

对某些特殊的引力波源而言，其引力辐射频率是受波源运动直接制约的，例如一个自转的脉冲星的引力辐射频率是其自转频率的两倍。但对大多数双星系统，引力辐射频率和其自然频率相关，自然频率定义为

$f_{0}={\sqrt {{\overline {\rho }} \over 4\pi }}$

这里${\overline {\rho }}$是波源的能量-质量的平均密度。对双星系统这个频率和其轨道频率有相同的数量级。

很显然波源的质量M和尺寸半径R决定了它的自然频率，对球体而言有${\overline {\rho }}={\frac {3M}{4\pi R^{3}}}$。对一个质量为1.4倍太阳质量，半径为10千米的中子星，其自然频率为1.9千赫兹；对一个质量为10倍太阳质量，视界半径为30千米的黑洞，其自然频率为1千赫兹；而对于质量为2.5×10⁶倍太阳质量，位于银河系中心的超大质量黑洞，其自然频率为4毫赫兹，因为其密度反而更低。从自然频率估计的引力辐射频率一般来说在數量級上是正确的，本质上是一个快捷但很粗略的估计，得到是其真实频率的上限。

重力波源

LIGO和LISA主要探测的波源频域分布。橫軸為頻率，縱軸為重力波振幅。

重力波的產生，是因為非對稱的運動造成了四極矩隨時間變化。籠統的說法是，只要一個系統在運動時輪廓變化了，就能夠生成重力波。例如，一支鉛筆的旋轉會否產生重力波，要看其旋轉軸：沿著鉛筆則無，垂直於鉛筆則有。另一個簡單的例子是啞鈴的旋轉。如果啞鈴的兩端好像兩個天體互相公轉（即旋轉軸垂直於連接啞鈴兩端的把手），它就會產生重力波。如果啞鈴的兩端質量極高，就可以模擬中子星或黑洞雙星系統。非對稱系統的質量越高，運動速度越高，其散發的重力波就會越強。

重力波的頻率取決於動態系統的特徵時間尺度。對於雙星系統，兩個天體相互公轉的頻率就是重力波的頻率。重力波源一般以頻帶分類。1至10 kHz的歸為高頻波源，來自於中子雙星、雙黑洞、超新星等等，這一頻率段在地基重力波探測器的偵測精度範圍以內。1 mHz至1 Hz的歸為低頻波源，來自於超重黑洞、矮雙星、白矮雙星等等，能用太空激光干涉儀和航天器多普勒跟蹤方法來偵測。1 nHz至1 mHz的歸為甚低頻波源，來自於超重黑洞、宇宙弦尖點（cosmic string cusp）等等，這是脈衝星計時實驗所研究的頻帶。最後10⁻¹⁸至10⁻¹⁵ Hz的歸為極低頻波源，對應於宇宙微波背景中所能探測到的重力波特徵。

双星系统的引力波

双星系统绕质心运动的示意图，在牛顿力学中这个轨道总是稳定的，但在相对论力学下引力辐射会造成轨道的缓慢收缩

能够辐射可观测量级引力波的密近双星系统包括白矮星、中子星和黑洞等致密恒星组成的双星系统，例如黑洞双星、黑洞-中子星、双中子星、双白矮星等等。它们具有很大且随时间变化的四极矩，对LIGO等地面探测器和空间探测器LISA而言都是重要的引力波源，也是至今唯一由间接观测证实的引力波源（PSR 1913+16）。从总体上看，双星系统的引力辐射过程实际是一个双星逐渐接近结合（coalescence）的过程，这一过程按顺序分为旋近（inspiral）-合并（merger）-自转减缓（ringdown）三相。点这里观看双星系统合并的示意影片

在旋近态中双星仅因为引力辐射损失动能，造成其轨道以很缓慢的速度发生衰减，两颗恒星逐渐接近；换句话说是它们发生引力辐射的时间尺度远大于其公转周期，因此这一过程被认为是绝热的，最常用的预测波形的方法即是后牛顿近似方法。从引力波的频率估算方法可知，双星系统的辐射频率与其自身密度的平方根成正比关系。地面探测器可探测的双星包括中子星和恒星质量黑洞，LISA则负责探测白矮星等未知双星和超大质量黑洞。假设两颗具有相同质量M的星体在半径为R的圆轨道上相互绕转，则系统具有非轴向速度$v^{2}={\frac {M}{4R}}\,$，由此估算得到的引力波振幅量级为

$h_{binary}\sim {\frac {1}{2}}{\frac {M}{r}}{\frac {M}{R}}$

其中r是波源到探测器的距离。 引力波的光度估算为

$L_{binary}\sim {\frac {1}{80G}}\left({\frac {M}{R}}\right)^{5}$

在国际单位制下，实际上的光度还需要再乘以被省略的系数$c^{5}/G=3.6\times 10^{52}\,$瓦特，相比之下，太阳的光度只有$3.8\times 10^{26}\,$瓦特。这意味着对于某些距离地球较近的双星，其向地球发射的引力波携带了比其发射的电磁波（光）更多的能量。
轨道运动辐射的能量会造成轨道的收缩，其结果是观测到发射的引力波频率随时间增长，这种波叫做啁啾（chirp）信号。估算得到的啁啾的时间尺度为

$t_{chirp}={\frac {Mv^{2}}{L_{binary}}}\sim 20M\left({\frac {M}{R}}\right)^{-4}$

计算可得这个时间尺度远大于双星的公转周期，因此可以认为旋近是一种绝热演化。 更精确的计算表明对于不等质量的双星，其四极矩的振幅和轨道收缩率与系统的啁啾质量有关，啁啾质量定义为

$M_{chirp}=\mu ^{3/5}M^{2/5}\,$

其中$\mu \,$是系统的折合质量，而M则是总质量。这实际表明是折合质量和总质量共同决定了双星系统的频率以多快的速度扫过频带。经详细计算得出的圆轨道双星系统的引力波振幅为

$h=2\left(4\pi \right)^{1/3}{\frac {G^{5/3}}{c^{4}}}f_{GW}^{2/3}M_{chirp}^{5/3}{\frac {1}{r}}$

其中$f_{GW}\,$是引力波的频率，计算并未考虑红移。对于更一般的椭圆轨道其形式更为复杂。
如果能够观测到啁啾的时间尺度，则可以推算出双星的啁啾质量；进而可以从啁啾质量和观测到的引力波振幅推算出双星到地球的距离，这意味着将有可能进一步借此测量哈勃常数和其他宇宙学常数。
随着双星系统的轨道衰减逐渐加快，绝热近似不再适用，这样双星系统进入合并态：两颗恒星接近后发生猛烈的接触合并成一个黑洞，并有相当部分的质量以引力波的形式释放（但也有很大一部分质量由于角动量守恒的制约无法离开黑洞视界，从而在黑洞附近形成吸积盘，一般说法认为这有可能会导致伽玛射线暴的形成），这里后牛顿近似方法不适用，参见“恒星质量黑洞的引力波”；这个合并形成的黑洞随后进入自转减缓态，随着引力辐射黑洞的自转频率逐渐降低，最后稳定成一个克尔黑洞。

本质上，双中子星在宇宙中的数量相对稀少，在可观测的范围内它们的数量要少于中子星-白矮星组成的双星系统，更少于宇宙中广泛存在的低频（$10^{-5}-10^{-1}Hz\,$）的双白矮星系统。这些双白矮星在数量上和寿命上都要远大于像PSR1913+16这样处于轨道收缩态的双中子星。这是由于大多数恒星都具有较小的质量，而大多数恒星又都是双星。在据估计LISA有可能发现上千个这样的双白矮星系统，其发现概率远大于地面探测器对双中子星的探测期望。不过事实上，银河系内太多的双白矮星系统会形成频率低于1毫赫兹的背景噪声，这种背景噪声叫做迷惑噪声（Confusion Noise），它将高于LISA本身的仪器噪声，但这些噪声不会影响对较强的黑洞信号的探测。而河外星系的双白矮星则由于振幅太低，尽管也能够形成高至1赫兹频率的背景噪声，其程度仍然远在LISA的仪器噪声之下。

脉冲星的引力波

蟹状星云，蓝色部分为钱德拉X射线天文台拍摄的X射线图像，红色部分为可见光图像，其星云中心附近存在一颗年轻的脉冲星PSR J0534 + 2200，是被寄予很大希望证实为引力波源的天体之一

对于一颗独立自转的中子星（脉冲星）而言，成为引力波源的必要条件为其质量（或质量流）分布存在不对称性，否则一个对称的球体自转时四极矩对时间的二阶偏导数为零。非对称性的来源机制包括两类。
第一种情形是相对于星体固定的非对称性，可能的机制包括

• 星体本身即是非完全对称的类球体（例如球状星团Terzan 5内部的脉冲星PSR J1748-2446ad，自转频率716赫兹，是已知自转最快的脉冲星）
• 脉冲星的磁场方向与其自转轴方向不一致（例如PSR1828-11）
• 恒星吸积导致的非对称性（典型例子即低质量X射线双星，例如天鹅座X-1）

假设一颗半径为R的中子星的自旋频率为f，并且在某个方向上具有使其形状不对称的质量m，其引力波辐射频率为自转频率的2倍，即2f。但脉冲星也有可能辐射其他频率的引力波，例如正在发生进动的脉冲星会同时发出频率为（或接近为）f和2f的引力辐射。由于脉冲星的自转频率是高度稳定的，其引力辐射的频率也高度稳定在一个很窄的频域内。从非轴向速度$v=2\pi Rf\,$估算得到其引力波振幅为

$h_{pulsar}\sim 2\left(2\pi Rf\right)^{2}m/r$

实际计算中常用的振幅公式为

$h_{pulsar}={\frac {16\pi ^{2}G}{c^{4}}}{\frac {\epsilon I_{zz}f^{2}}{r}}$

其中$I_{zz}\,$是星体相对于自转轴的转动惯量，$\epsilon =(I_{xx}-I_{yy})/I_{zz}\,$是星体的非对称性，r是源点到场点的距离。 由此得到的光度为

$L_{pulsar}\sim {\frac {1}{5}}\left(2\pi f\right)^{6}m^{2}R^{4}$

这一辐射能量如果认为将完全来源于星体的自转能量，则估算出的星体自转减慢（spindown）态的时间尺度为

$t_{spindown}={\frac {1}{2}}mv^{2}/L_{pulsar}\sim {\frac {5}{4\pi }}f^{-1}\left({\frac {m}{R}}\right)^{-1}v^{-3}$

现在一般认为中子星的壳层不足以支持质量超过$10^{-5}\,$倍太阳质量的非对称性，例如LIGO的预期波源，PSR J2124-3358，其估算出的非对称性上限为总质量的$1.1\times 10^{-7}\,$。从这一点估算出的自转减慢态的时间尺度比实际长太多。因此看来引力辐射并不足以成为中子星自转减慢的主要原因。 以蟹状星云内部的年轻脉冲星PSR J0534 + 2200为例，其非对称性小于总质量的$3\times 10^{-4}\,$，引力波的振幅上限约为$6\times 10^{-25}\,$；而对于较老的毫秒脉冲星，非对称性只有总质量的$10^{-9}\,$左右，如果距离地球1秒差距，估算得到的振幅上限量级为$10^{-28}\,$，虽然这些典型的振幅都远低于LIGO的灵敏度，但通过较长时间的相关测量则可以找到其对应的相关信号。
第二种情形是非对称的部分相对于星体是运动的，典型的例子即是中子星r模式的不稳定性，也被称作中子星上的罗斯比波（Rossby Wave），这个名称来源于其机制类似于地球表面的科里奥利力。这种情形下的引力辐射频率理论上与中子星自转频率的关系近似为

$\omega =-{\frac {(l-1)(l+2)}{l+1}}\Omega \,$

这实际是连带勒让德方程的本征值。对于四极矩展开项$l=2\,$，可得引力辐射频率是自转频率的4/3倍。

引力坍缩和伽玛射线暴的引力波

中子星的形成来源于超新星的引力坍缩，超新星内核的坍缩速率可达每秒七万千米。这种引力坍缩并不是高度对称的，这一点已经在对超新星SN 1987A的观测中得到证实。因此这种引力坍缩会产生一种持续时间很短且无周期性的引力波的突发信号（burst），并伴随有电子俘获和中微子输运的过程。但引力辐射的波形和振幅都很难从理论上预测，一般认为只有数值模拟的方法。这种突发信号可能频带很宽，中心频率在1千赫兹；或者有可能是在100赫兹到10千赫兹之间任意一个频率的周期性啁啾信号。理论上估计如果其发射的能量要大于0.01倍太阳质量，现在的地面探测器则有可能观测到发生在室女座星系团之内的这类事件。但事实上到底有多大比例的能量在辐射中被释放仍然是一个未能解决的问题，现在一般认为辐射能量不会超过超新星总质量的$10^{-6}\,$，这样看来当前的探测器还没有能力探测到河外星系内的超新星爆发。不过这类事件在银河系内的发生概率大概有几十年一次，计算得到其对应距离为10千秒差距的引力坍缩辐射的引力波振幅约为$10^{-20}\,$，持续时间为几个毫秒，新一代地面探测器的灵敏度应该可以达到相应的水平。

大质量恒星坍缩为黑洞的过程是伽玛射线暴的产生原因吗？

伽玛射线暴是短时间（几毫秒至几分钟）内极高强度的伽玛射线辐射，按持续时间分为长短两类。从大多数观测得出的结论支持伽玛射线暴是伴随高速自转的黑洞的诞生而产生的说法，果真如此的话这种高速自转的非对称性结构将有可能形成相对于引力坍缩高度稳定的引力辐射，因而有可能在观测到其明亮的电磁辐射的同时探测到相应的引力辐射。不过这种事件应该并不多见，因而需要一个很广的观测距离（至少约3吉秒差距），以及相当比例的辐射能量。不过于2007年2月发生的一次短伽玛射线暴，来自仙女座星系方向的GRB070201，并没有被LIGO在S5中探测到有引力辐射的存在。这可能是因为GRB070201发生在比仙女座星系更遥远的地方，但也可能暗示着伽玛射线暴并非源于黑洞或中子星的形成过程，而来自如磁星这样带有极强磁场的软伽玛射线复发源。

恒星质量黑洞的引力波

天文学家现在认识到宇宙中存在数量丰富的黑洞，通过对电磁波谱的观测已经确认了某些存在于银河系内X射线双星系统内的恒星质量黑洞，以及某些著名的河外星系中心的超大质量黑洞。这两类黑洞的质量非常不同，也造成它们的引力辐射的机制和频率存在很大差别：恒星质量黑洞一般具有10倍左右太阳质量，一般形成于红巨星或超新星爆发时内部的引力坍缩；大质量和超大质量黑洞的质量则在$10^{5}-10^{10}\,$倍太阳质量范围内，其形成机制至今还不十分清楚。黑洞的视界半径$R=2M\,$，则其自然频率由下式决定：

$h_{BH}\sim 2800\left(M/10M_{\odot }\right)^{-1}Hz\,$

这表明黑洞双星的自然频率和其质量成反比。恒星质量黑洞的引力波频率在地面探测器所观测的范围内，而超大质量黑洞的引力波只能从LISA这样的空间探测器捕捉到。

NASA超级计算机模拟得到的黑洞双星开始合并的情形

恒星质量黑洞的引力辐射一般认为来源于双星系统（其中至少有一个是黑洞）的旋近-合并-自转减缓这一系列过程，这和双中子星等其他双星系统的引力波辐射机制是相同的。在旋近态中，两个黑洞的距离相当远（$r>>4M\,$），并以很缓慢的速度逐渐接近。如果黑洞系统的可观测性完全依赖于伴随着轨道衰减产生的引力辐射，那么和所有双星系统一样，后牛顿近似完全足够解决此类问题。不过当黑洞双星的距离逐渐拉近，直到其轨道缩减为最内稳定圆轨道（Innermost Stable Circular Orbit，简称ISCO）时，黑洞掉入彼此的视界之内，双星从旋近态向合并态转变。这种相变是完全的相对论效应，在牛顿力学中不会有此情况出现，因此后牛顿近似在这里完全不适用。黑洞的合并必然会伴随有引力波的突发信号放出，在目前分析这种信号只能采用数值相对论模拟的方法，并且有很多实际计算困难。而且对于质量超过50倍太阳质量的黑洞，旋近态终止时的频率是最后稳定轨道的公转频率，这个值大概只有黑洞自然频率的0.06倍，约30赫兹。这个频率已经接近地面探测器的低频极限，即使仅是探测到此类事件也需要对波形进行一些预测，因而黑洞合并数值模拟的结果对这种引力波的探测有重要意义。合并后系统进入自转减缓态，两个黑洞的视界合并成一个，黑洞双星以类似阻尼振动的形式放出引力辐射，逐渐稳定为一个单独的克尔黑洞，此过程的时空度规可以用对克尔时空的线性微扰理论解出。自转减缓态的一个特征是它具有在数学上为复数的自转频率，即复数频率的实部是特征频率，虚部是阻尼因子；理论上克尔黑洞的质量和角动量完全决定了所有可能的复数频率，这些频率是离散的并且有无穷多个，统称为黑洞的准简正模式（Quasi-normal modes），而黑洞的自转则可用这些准简正模式的线性叠加来描述。

虽然宇宙间黑洞的数量要低于中子星，但据估计在空间尺度上两个黑洞构成的双星系统数量反而要比中子星的双星系统多，主要是因为中子星的双星系统相对黑洞双星系统而言不容易形成。有说法认为球状星团是形成黑洞双星的高效工厂，如果事实如此，那么宇宙间黑洞双星的数量可能会比中子星双星的数量高十倍左右。由于球状星团内部的黑洞质量大于恒星的平均质量，黑洞会逐渐向星团中心运动，在中心三体的相互作用是双星形成的主要机制。值得注意的是，这类双星系统与球状星团的引力束缚并不强，其结果就是双星有可能脱离星团开始独立演化，其稳定时间一般在$10^{10}\,$年之内。现在的研究对于恒星质量黑洞的合并几率还不很确定，但一般认为在15兆秒差距的范围内每年至少会发生几次。

甚至有推测认为，黑洞双星有可能是宇宙间暗物质的一部分：朝大麦哲伦星云方向的微引力透镜观测表明银河系的星系晕中有相当部分由大质量致密晕天体（MACHOs）构成，这些天体几乎不放出任何电磁辐射，因此探测它们只能依靠微引力透镜等手段。现在还不十分清楚这些存在于星系晕的晕族大质量致密天体到底是什么，有可能是黑洞、中子星或褐矮星。据认为有多至一半的星系晕可能来源于质量为0.5倍太阳质量的致密暗物质天体。这一推测从恒星演化的角度来看很难理解，因为黑洞和中子星的质量要大于0.5倍太阳质量，而具有此种质量的白矮星应该足够亮到可以被识别为引力透镜的程度。一种可能的解释是在能够形成黑洞的外界条件下由于恒星质量较低因而形成了这类小质量的致密星体。如果这种解释正确，则人类可期望观测到在这类星体周围的一系列双星的合并，并且在一个星系内双星的合并几率可达到每20年出现一次，高于超新星爆发的几率。

大质量和超大质量黑洞的引力波

哈勃太空望远镜拍摄的双天线星系，星系的碰撞很有可能导致其中心超大质量黑洞的合并

参见：超大质量黑洞

来自大质量和超大质量黑洞（即“星系质量”）的引力辐射存在两种形式：一种是超大质量黑洞的合并，即恒星质量黑洞合并的加强版，由于质量很大引力辐射的频率很低，但振幅却相当高。因为有效信号振幅和黑洞质量基本成近似线性关系，在相同距离下质量为$10^{6}\,$倍太阳质量的大质量黑洞的引力辐射振幅约为10倍太阳质量的黑洞引力辐射的$10^{5}\,$倍（$h\sim 10^{-17}\,$）。这意味着空间探测器对于这类信号会具有非常高的信噪比，无论这类波源位于宇宙间哪个角落。现在一般认为在大多数星系中心都存在质量至少在$10^{6}\,$倍太阳质量以上的大质量或超大质量黑洞，它们被认为是类星体和活动星系的动力源，并有证据表明超大质量黑洞的质量与其宿主星系核的质量成正比关系。与恒星不同，星系的尺寸对于星系群内邻近成员的间距而言不是那么微不足道，两者甚至可以达到同一数量级，因此星系之间发生碰撞的概率相当高，典型的例子是乌鸦座的双天线星系（Antennae Galaxies），它是由两个正在发生碰撞的星系NGC 4038和NGC 4039形成的。星系的碰撞主要是引力的相互作用，没有恒星物质的实际接触，并且由于受角动量守恒限制，两个星系发生正碰的可能性不大，这意味着位于星系中心的黑洞很难与另一个星系中心的黑洞直接发生合并。不过仍然由于黑洞质量大于恒星的平均质量，它们会逐渐向碰撞后的星系中心漂移并最终发生碰撞，这一机制说明宇宙间超大质量黑洞合并的几率是相当高的。

小质量致密天体与星系中心的大质量黑洞形成的EMRI是LISA重要的探测波源之一

主条目：极端质量比例旋

另一种情形是大质量黑洞对小质量致密天体的俘获所释放的引力辐射，这里的小质量致密天体包括白矮星、中子星、恒星质量黑洞和中等质量黑洞，这被称作极端质量比例旋（Extreme Mass Ratio Inspiral, EMRI）。而主序星和巨星由于并不那么致密，一般认为当它们接近黑洞时，来自黑洞引力场的潮汐力将对恒星表面物质产生吸积，从而激发这些物质表现出类星体现象。当一个致密星体碰巧接近星系中心的超大质量黑洞时它有可能被俘获，在围绕着超大质量黑洞公转的同时放出引力辐射，因此这也是一种旋近态。不过由于两者质量比例悬殊，这种旋近态的变化比一般的双星系统更为缓慢，从观测的角度来说，这意味着可以用长达数年的时间观测到同一种波形。这种引力辐射可近似为从一个克尔黑洞附近的一个质点放射出的啁啾信号，而质点的轨道有可能是高度偏心的（偏心率接近1）。随着引力辐射系统动能不断减少，这使得轨道的偏心率逐渐降低，在旋近态的后期有可能降低到0.4左右，在这段时间内EMRI的辐射频率稳定在LISA的测量频域之内。其波形包含了黑洞附近的时空几何信息，尤其有可能通过对黑洞质量和自旋的观测来验证黑洞的唯一性定理（无毛定理）。

EMRI的发生率与星系的构成方式关系不大，这使得LISA在一年的时间内有能力观测到这类事件上百次，距离最近的事件有可能在红移小于0.1之内，前提是理论研究能够对质点运动的轨道在数十个周期内做出较为精确的预测。但在理论上预测这种轨道并不那么容易，主要原因在于围绕克尔黑洞的高度偏心轨道有可能是混沌的，如果质点的运动轨迹远离黑洞的赤道平面轨道将变得非常复杂，有可能在整个视界内高速游荡。想要准确预测数十个周期内的轨道运动，需要定义好的初始条件以及多达14个用来区分不同运动且足够精确的参数，这就导致探测筛选这种信号需要一组数量非常庞大的波形模板，完全计算这些模板甚至超越了现有计算机的计算能力，这导致单纯的模式匹配算法很可能并不适用于此。至今最常见的EMRI波形的数值解法是由康奈尔大学的索尔·图科斯基（Saul Teukolsky）于二十世纪七十年代创立的图科斯基方程。

图科斯基方程在克尔几何的框架下应用微扰数值求解爱因斯坦场方程，实际对任何种类的微扰场都适用，其形式为

$\left[{\frac {r^{2}+a^{2}}{\Delta }}-a^{2}\sin ^{2}\theta \right]{\frac {\partial ^{2}\psi }{\partial t^{2}}}+{\frac {4Mar}{\Delta }}{\frac {\partial ^{2}\psi }{\partial t\partial \phi }}+\left[{\frac {a^{2}}{\Delta }}-{\frac {1}{\sin ^{2}\theta }}\right]{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}-\Delta ^{-s}{\frac {\partial }{\partial r}}\left(\Delta ^{s+1}{\frac {\partial \psi }{\partial r}}\right)$

$-{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right)-2s\left[{\frac {a(r-M)}{\Delta }}+{\frac {i\cos \theta }{\sin ^{2}\theta }}\right]{\frac {\partial \psi }{\partial \phi }}$

$-2s\left[{\frac {M\left(r^{2}-a^{2}\right)}{\Delta }}-r-ia\cos \theta \right]{\frac {\partial \psi }{\partial t}}+s\left[s\cot ^{2}\theta -1\right]\psi =4\pi \Sigma {\mathcal {T}}$

其中s叫做自旋权重（spin weight），是一个与微扰场的自旋有关的量，在引力场的微扰下$s=\pm 2\,$；方程中其他物理量的含义请参考克尔度规。方程在频域内可作分离变量，现已用数值方法找到了各种特殊情形下的特解，所得的数值结果被统称为TB (Teukolsky-based)波形。

大爆炸的引力波

基于暴脹理论的星系起源，星系起源于最初质量密度的微扰，而这些微扰形成了今天的引力随机背景辐射

引力波自诞生起在宇宙中的传播至今就几乎没有衰减或散射，从引力子的角度看，是因为引力子具有非常小的散射截面。宇宙微波背景辐射揭示了大爆炸之后$10^{5}\,$年的宇宙状况，对太初核合成的研究揭示了大爆炸之后几分钟内的宇宙状况，而引力波的诞生则可以追溯到大爆炸之后小于$10^{-24}\,$秒的时间范围之内。对这种引力随机背景辐射（stochastic background radiation）的观测是引力波天文学最重要的课题之一。

与一般情形下的引力波用平均振幅描述不同，引力波的随机背景辐射通常用波场的能量密度描述，这种随机背景辐射可以来自任何天体（例如双白矮星等双星发出的迷惑噪声），也可以来自大爆炸。对于宇宙学中的场，一般要将这个场的能量密度归一化到宇宙的临界密度，由此定义

$\Omega _{GW}\equiv {\frac {1}{\rho _{c}}}{\frac {d\rho _{GW}(f)}{d\ln f}}$

这个量描述了随机引力波的能量密度按频率分布情况，则引力背景辐射的总能流密度由对$\Omega _{GW}\,$从频率0至正无穷的积分给出。$\rho _{c}=3H^{2}/8\pi G\,$是弗里德曼方程下得到的宇宙临界密度值；H是哈勃常数，如果以千米/秒·兆秒差距为单位，现在一般认为这个值在50到65之间。尽管现在还不确定引力波场的能量密度的具体数值，在当代宇宙学的框架下背景辐射的能量密度受到太初核合成、微波背景辐射以及脉冲星计时的约束：太高的能流密度会破坏太初核合成理论的成立，太高的能量涨落则与实际各向异性非常小的微波背景辐射不符，而对毫秒脉冲星计时的观测证实了引力波的背景辐射强度不足以高到使脉冲星信号间隔发生可观测变化的程度。

早期宇宙的暴脹是一个令人感兴趣的图景，在暴脹模型中，引力子在普朗克时期内产生，并有可能按照引力场和其他场的自由度均分，这就形成了其温度相当于微波背景辐射的引力波的热背景辐射。其后宇宙进入暴脹时期，暴脹对最初质量密度的形成提供了足够大的微扰，这种机制使星系能够形成。而这些微扰则以引力场微扰的形式传播至整个宇宙形成了随机背景辐射。引力波形成的随机背景辐射被认为是各向同性、静态且无偏振的。而暴脹理论预言下的频谱是平坦的，即能量密度与频率无关。宇宙背景探测者（COBE）通过对微波背景辐射的观测得到在频率为$10^{-18}\,$赫兹处的能量密度上限为$3\times 10^{-14}$，如果暴脹理论是正确的，这意味着对所有频率的背景辐射都具有相同的能量密度，这样低的能量密度导致现有的任何探测器都无法捕捉到暴脹的引力波信号。在不同于暴脹的其他模型下，例如宇宙弦（cosmic string）的振动也会产生能量密度与频率无关的引力辐射，而宇宙弦预言下的能量密度达到了当前可观测的量级。

对于这种信号LIGO在频率100赫兹的灵敏度为$10^{-5}\,$，但通过对两个探测器（例如LHO和LLO，或者LIGO和VIRGO，GEO600等）符合测量得到的结果进行互相关计算可提高到$10^{-6}\,$，因此互相关是搜寻此信号的重要手段。而Advanced LIGO在这个频率上的灵敏度预计可达到$10^{-9}\,$；LISA在频率1毫赫兹的灵敏度可达$10^{-8}\,$，但在实际观测中能否达到这个数值取决于双白矮星等产生的背景噪声是否会将随机宇宙背景辐射淹没。除此之外，r模式的中子星、双中子星和黑洞以及某些超新星爆发都有可能将频率高于0.1毫赫兹的宇宙背景辐射淹没。一般认为来自双星的背景噪声在低于10微赫兹的频率下快速降低，因此微赫兹量级的空间探测器可能是探测宇宙随机背景辐射的最佳手段。

理論

阅读本节需要了解电动力学和广义相对论的基本概念，可直接参阅有关书籍。

线性爱因斯坦方程

引力波——时空的波纹（示意图）

广义相对论预言下的引力波是以波形式传播的时空扰动，被形象地称为“時空漣漪”。广义相对论下的弱引力场可写作对平直时空的线性微扰：（以下采用自然单位，引力常数G和光速c都設為1）

$g_{\alpha \beta }=\eta _{\alpha \beta }+h_{\alpha \beta }$，其中$|h_{\alpha \beta }|\ll 1$

这里$\eta _{\alpha \beta }=diag(-1,1,1,1)$是平直时空的闵可夫斯基度规，$h_{\alpha \beta }$是弱引力场带来的微扰。在这个度规下计算得到的黎曼张量为

$R_{\alpha \beta \mu \nu }={\frac {1}{2}}\left(\partial _{\mu }\partial _{\beta }h_{\alpha \nu }-\partial _{\mu }\partial _{\alpha }h_{\beta \nu }+\partial _{\nu }\partial _{\alpha }h_{\beta \mu }-\partial _{\nu }\partial _{\beta }h_{\alpha \mu }\right)$

爱因斯坦张量为

$G_{\alpha \beta }=-{\frac {1}{2}}\left(\partial _{\mu }\partial ^{\mu }{\overline {h}}_{\alpha \beta }+\eta _{\alpha \beta }\partial ^{\mu }\partial ^{\nu }{\overline {h}}_{\mu \nu }-\partial _{\beta }\partial ^{\mu }{\overline {h}}_{\alpha \mu }-\partial _{\alpha }\partial ^{\mu }{\overline {h}}_{\beta \mu }\right)$

这里${\overline {h}}_{\alpha \beta }=h_{\alpha \beta }-{\frac {1}{2}}\eta _{\alpha \beta }h$，$h=\eta ^{\alpha \beta }h_{\alpha \beta }$，${\overline {h}}_{\alpha \beta }$被称作迹反转度规微扰（trace-reverse metric perturbation）。

如果采用洛伦茨规范，爱因斯坦张量的后三项将为零，这里洛伦茨规范的形式为

$\partial ^{\beta }{\overline {h}}_{\alpha \beta }=0$

事实上总可以选择这样的规范条件，并且洛伦茨规范不是唯一的，意味着坐标在一个无穷小的线性坐标变换下仍满足洛伦茨规范，关于这一点请参考有关规范变换的内容。

在洛伦茨规范下，爱因斯坦张量为

$G_{\alpha \beta }=-{\frac {1}{2}}\partial _{\mu }\partial ^{\mu }{\overline {h}}_{\alpha \beta }=-{\frac {1}{2}}\Box ^{2}{\overline {h}}_{\alpha \beta }$

代入爱因斯坦引力场方程$G_{\alpha \beta }=8\pi T_{\alpha \beta }$，

$\Box ^{2}{\overline {h}}_{\alpha \beta }=-16\pi T_{\alpha \beta }$

这个方程又叫弱引力场中的线性爱因斯坦方程。在远源（$T_{\alpha \beta }=0$）的情形下，得到带有达朗贝尔算符的四维波方程：

$\Box ^{2}{\overline {h}}_{\alpha \beta }=0$

引力波的传播

上面波方程的一般解为如下本征函数的线性叠加：

${\overline {h}}_{\alpha \beta }=A_{\alpha \beta }\exp {\left(i\mathbf {k\cdot x} \right)}$

其中$A_{\alpha \beta }$是四维振幅，$\mathbf {k}$是四维波矢，满足条件

$\eta _{\alpha \beta }k^{\alpha }k^{\beta }=0$，这表明引力波传播经过的测地线是零性的，即其传播速度是光速。

四维波矢$k^{\alpha }=\left(\omega _{\vec {k}},{\vec {k}}\right)$，其中$\omega _{\vec {k}}$是波的角频率，${\vec {k}}$是经典的三维波矢。由于洛伦茨规范并不唯一，此时坐标还不是完全确定的。如果再加上条件：

${\overline {h}}_{ti}=0$

$\eta _{\alpha \beta }{\overline {h}}^{\alpha \beta }=0$

第一个条件表示引力波张量中所有与时间t有关的分量都为零，第二个条件表示引力波张量矩阵的迹为零。因此这组规范条件叫做转置无迹规范（transverse traceless gauge），简称TT规范。在TT规范下，${\overline {h}}_{\alpha \beta }=h_{\alpha \beta }$。 由洛伦茨规范和TT规范共同决定下的引力波张量只有两个分量是独立的，它们实际对应着引力波的两种偏振态。对于在z方向传播的波矢$k^{\alpha }=\left(\omega ,0,0,\omega \right)$，这两个振动分量垂直于传播方向，这表明引力波和电磁波一样是横波，其张量形式写作

引力波的$h_{+}$偏振对质点位置的调制

引力波的$h_{\times }$偏振对质点位置的调制

$h_{\alpha \beta }={\begin{pmatrix}0&0&0&0\\0&h_{+}&h_{\times }&0\\0&h_{\times }&-h_{+}&0\\0&0&0&0\end{pmatrix}}$

$h_{+}$ 和 $h_{\times }$是引力波的两种偏振态，右图中示意了两种偏振各自不同的振动形式。

引力波的辐射

有源的线性爱因斯坦方程解释了波源的运动如何产生引力辐射：

$\Box ^{2}{\overline {h}}^{\alpha \beta }=-16\pi T^{\alpha \beta }$

类似用泊松方程求解牛顿引力势，运用格林函数可得到带有推迟势的一般解：

${\overline {h}}^{\alpha \beta }\left(t,{\vec {x}}\right)=4\int \operatorname {d} ^{3}x^{\prime }{\frac {T^{\alpha \beta }\left(t-|{\vec {x}}-{\vec {x}}^{\prime }|,{\vec {x}}^{\prime }\right)}{|{\vec {x}}-{\vec {x}}^{\prime }|}}$

这里$T^{\alpha \beta }$所处在的时间是$t-|{\vec {x}}-{\vec {x}}^{\prime }|$，表示引力波从源点${\vec {x}}^{\prime }$传播到场点${\vec {x}}$经过了时间为$|{\vec {x}}-{\vec {x}}^{\prime }|$的延迟。

在远场近似和长波极限下，格林函数解近似为

${\overline {h}}^{\alpha \beta }\left(t,{\vec {x}}\right)\approx {\frac {4}{r}}\int \operatorname {d} ^{3}x^{\prime }T^{\alpha \beta }\left(t-r,{\vec {x}}^{\prime }\right)$

其中标量$r=|{\vec {x}}-{\vec {x}}^{\prime }|\approx |{\vec {x}}|$是源点到场点的距离。

相对论中波源的质能守恒和动量守恒合起来写作

$T_{,\beta }^{\alpha \beta }=0$

因此动量-能量张量$T^{\alpha \beta }$中的$T^{tt}$（质量-能量密度）和其他所有和时间t有关的分量$T^{it}$（动量密度）对时间的偏导数都为零，代入后方程的解可进一步化简为

${\overline {h}}^{\alpha \beta }={\frac {2}{r}}{\frac {\operatorname {d} ^{2}Q^{\alpha \beta }\left(t-r\right)}{\operatorname {d} t^{2}}}$

这即是引力辐射的四极矩近似公式，描述了一个弱相对论系统引力辐射的最基本情形。其中$Q^{\alpha \beta }$描述了波源的质量-能量分布

$Q^{\alpha \beta }=\int \rho x^{\prime \alpha }x^{\prime \beta }\operatorname {d} ^{3}x^{\prime }$

这里张量$Q^{\alpha \beta }$即是系统的质量四极矩（转动惯量张量），而$\rho \equiv T^{tt}$是波源的质量-能量密度，积分范围是整个波源内部。

四极矩公式的物理意义是引力辐射起始于随时间二阶变化（例如谐振）的四极矩，这一点与电磁辐射不同：电磁辐射起始于随时间二阶变化的偶极矩。这一区别的来源是：一个随时间二阶变化的电偶极矩或磁偶极矩对应着电荷密度中心的振动，这一振动是随意不受限制的；而一个随时间二阶变化的质量的偶极矩对应着质心的振动，这一振动不能满足动量守恒定律，因此不存在这样对时间二阶偏导不为零的质量偶极矩。由于四极矩是偶极矩的更高阶项，这也是引力辐射要远弱于电磁辐射的原因。

引力波的能量

四极矩近似下引力波的光度（总辐射功率）为

$L_{GW}={\frac {1}{5}}\left(\sum _{i,j}{\frac {\operatorname {d} ^{3}Q_{ij}}{\operatorname {d} t^{3}}}{\frac {\operatorname {d} ^{3}Q_{ij}}{\operatorname {d} t^{3}}}-{\frac {1}{3}}\left({\frac {\operatorname {d} ^{3}Q}{\operatorname {d} t^{3}}}\right)^{2}\right)$

这里Q是张量矩阵$Q_{ij}$的迹。 引力波的能量通量（单位面积的辐射功率）近似为

$F_{GW}\sim |{\dot {h}}|^{2}\sim f^{2}h^{2}$

这里f是单色引力波的频率。

假设对于一束频率为1000赫兹，到达地球时的应力强度$h=10^{-22}$的引力波，可得其能量通量约为$3\times 10^{-3}W/m^{2}$，这比满月时地球上接收到的电磁辐射的能量通量还要大两倍，是全天最亮的恒星天狼星到达地球的电磁辐射能量的约一万倍。这表明引力波实际可以携带很大的能量，但与物质相互作用力非常小，这才是引力波难以被探测的根本原因。

參見

• 廣義相對論
• 引力場
• 重力磁性
• 引力子
• 引力波天文學
• 霍金輻射
• 激光干涉重力波天文台（LIGO）
• 線性化愛因斯坦場方程
• 激光干涉空間天線（LISA）
• 軌道共振
• 潮汐力

延伸閱讀

• Chakrabarty, Indrajit, "Gravitational Waves: An Introduction". arXiv:physics/9908041 v1, Aug 21, 1999.
• Landau, L. D. and Lifshitz, E. M., The Classical Theory of Fields (Pergamon Press),(1987).
• Will, Clifford M., The Confrontation between General Relativity and Experiment. Living Rev. Relativity 9 (2006) 3.
• Peter Saulson, "Fundamentals of Interferometric Gravitational Wave Detectors", World Scientific, 1994.
• J. Bicak, W.N. Rudienko, "Gravitacionnyje wolny w OTO i probliema ich obnarużenija", Izdatielstwo Moskovskovo Universitieta, 1987.
• A. Kułak, "Electromagnetic Detectors of Gravitational Radiation", PhD Thesis, Cracow 1980 (In Polish).
• P. Tatrocki, "On intuitive description of graviton detector", www.philica.com .
• P. Tatrocki, "Can the LIGO, VIRGO, GEO600, AIGO, TAMA, LISA detectors really detect?", www.philica.com .

書目

• Berry, Michael, Principles of cosmology and gravitation (Adam Hilger, Philadelphia, 1989). ISBN 0-85274-037-9
• Collins, Harry, Gravity's Shadow: the search for gravitational waves, University of Chicago Press, 2004.
• P. J. E. Peebles, Principles of Physical Cosmology (Princeton University Press, Princeton, 1993). ISBN 0-691-01933-9.
• Wheeler, John Archibald and Ciufolini, Ignazio, Gravitation and Inertia (Princeton University Press, Princeton, 1995). ISBN 0-691-03323-4.
• Woolf, Harry, ed., Some Strangeness in the Proportion (Addison–Wesley, Reading, Massachusetts, 1980). ISBN 0-201-09924-1.

外部鏈接

• 《大英百科全书》中的条目：Gravitational waves（英文）
• Gravitational Waves，In Our Time (BBC Radio 4)的《In Our Time》節目。(現在聆聽)
• The LISA Brownbag – Selection of the most significant e-prints related to LISA science
• Astroparticle.org. To know everything about astroparticle physics, including gravitational waves
• Caltech's Physics 237-2002 Gravitational Waves by Kip Thorne Video plus notes: Graduate level but does not assume knowledge of General Relativity, Tensor Analysis, or Differential Geometry; Part 1: Theory (10 lectures), Part 2: Detection (9 lectures)
• www.astronomycast.com January 14, 2008 Episode 71: Gravitational Waves
• Laser Interferometer Gravitational Wave Observatory. LIGO Laboratory, operated by the California Institute of Technology and the Massachusetts Institute of Technology
• The LIGO Scientific Collaboration
• Einstein's Messengers – The LIGO Movie by NSF
• Home page for Einstein@Home project, a distributed computing project processing raw data from LIGO Laboratory, searching for gravitational waves
• The National Center for Supercomputing Applications – a numerical relativity group
• Caltech Relativity Tutorial – A basic introduction to gravitational waves, and astrophysical systems giving off gravitational waves
• Resource Letter GrW-1: Gravitational waves – a list of books, journals and web resources compiled by Joan Centrella for research into gravitational waves
• Mathematical and Physical Perspectives on Gravitational Radiation – written by B F Schutz of the Max Planck Institute explaining the significance and background of some key concepts in gravitational radiation
• Binary BH Merger – estimating the radiated power and merger time of a BH binary using dimensional analysis