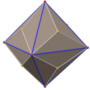
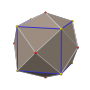
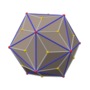
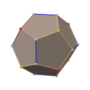
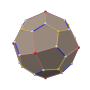
四角化菱形十二面体

四角化菱形十二面体图
四角化菱形十二面体图
度分布	4 (12个); 6 (8个); 8 (6个);
顶点	26
边	72
半径	4
直径	4
围长	3
色数	3
对偶图	大斜方截半立方体图
属性	平面, 可积（英语：Integral graph）
	查; 论; 编;

四角化菱形十二面体
	; （按这里观看旋转模型）
类别	卡塔兰立体
对偶多面体	大斜方截半立方体
识别
鲍尔斯缩写; （verse-and-dimensions的wikia：Bowers acronym）	siddykid
数学表示法
考克斯特符号; （英语：Coxeter-Dynkin diagram）
康威表示法	mC
性质
面	48
边	72
顶点	26
欧拉特征数	F=48, E=72, V=26 （χ=2）
二面角	155° 4' 56";
组成与布局
面的种类	; 不等边三角形
面的布局; （英语：Face configuration）	V4.6.8
顶点图	V4.6.8
对称性
对称群	Oh, B3, [4,3], *432
旋转对称群; （英语：Rotation_groups）	O, [4,3]+, (432)
特性
	凸、面可递
图像
	; V4.6.8; （顶点图）
; 大斜方截半立方体; （对偶多面体）	; （展开图）
	查; 论; 编;

在几何学中，四角化菱形十二面体是一种由48个不等边三角形组成的卡塔兰多面体，又称为六八面体（hexoctahedron）^[1]^[2]、六角化八面体（hexakis octahedron^[3]^[4]^[5]^[6]）、八角化立方体（octakis cube、octakis hexahedron）、菱形四角化十二面体（kisrhombic dodecahedron^[8]），虽然其具有面可递的性质，然而由于其组成的面不是正多边形因此不能算是正多面体^[9]，其对偶多面体为大斜方截半立方体。

性质

四角化菱形十二面体是卡塔兰立体的一种^[10]，即阿基米德立体的对偶多面体^[11]，其对应的阿基米德立体为大斜方截半立方体^[12]^[13]。并具有面可递的性质，这意味著，这立体上的任意两个面A和B，透过旋转或镜射这个立体，使A移动到B原来的位置时，其面仍然占据了相同的空间区域^[14]。所有的正多面体都拥有这个特性，然而四角化菱形十二面体并未所有边等长、组成的面也非正多边形，因此不属于正多面体^[9]。

组成

四角化菱形十二面体共由48个面、72个边、26个顶点组成，其中48个面为全等的三角形、72条边则有3种长度，每个长度各24条、26个顶点当中，有12个四面角顶点、8个六面角顶点、和 6个八面角顶点^[15]。

四角化菱形十二面体可以将菱形十二面体透过四角化变换来完成，其等价于将菱形十二面体每个面替换成一个顶点和四个三角形^[9]或在菱形十二面体的每个面上叠上一个菱形锥来组成四角化菱形十二面体。

体积与表面积

一个最短边边长为单位长的四角化菱形十二面体，其表面积A、体积V为^[16]：

{\begin{aligned}A&={\tfrac {6}{7}}{\sqrt {783+436{\sqrt {2}}}}\,a^{2}\\V&={\tfrac {1}{7}}{\sqrt {3\left(2194+1513{\sqrt {2}}\right)}}a^{3}\end{aligned}}

对称性

四角化菱形十二面体具有O_h, B₃, [4,3] (*432)的八面体群对称性（英语：Octahedral_symmetry）。其每条棱皆代表八面体群对称性的镜射线。其结构也可以透过将立方体在每个正方形面上以正方形的顶点、边中点和几何中心为基准将正方形分成8个三角形、或透过将正八面体在每个三角形面上以正三角形的顶点、边中点和几何中心为基准将正三角形分成6个三角形、或透过将菱形十二面体在每个菱形面上以菱形的几何中心为基准将菱形分成四个三角形来看出。^[17]

四角化菱形十二面体	球面镶嵌	立方体	正八面体	菱形十二面体

球极投影

与四角化菱形十二面体对应的球面镶嵌可透过透过9个球面大圆来构建^[18]（即四角化菱形十二面体投影到球面的结果）^[10]，因此在球极平面投影中，四角化菱形十二面体的棱可以在平面上形成9个圆或中心径向线。这9个圆或中心径向线可以分成两组，其中一组由3个圆或中心径向线组成（下图以紫色表示）、另一组由6个圆或中心径向线组成（下图以红色表示），分别代表其两个正交子群，分别是[2,2]（英语：Dihedral_symmetry_in_three_dimensions）和[3,3]（英语：tetrahedral symmetry）：

球极投影
平行投影		球极平面投影
图像
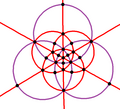
投影对称性		[4]	[3]	[2]

正交投影

四角化菱形十二面体及其对偶多面体大斜方截半立方体存在多个能投影出对称正交投影的投影方向。前两者的对偶图其对称性对应于A₂和B₂的考克斯特平面（英语：Coxeter plane）^[19]^[20]。

正交投影
投影对称性	[4]	[3]	[2]	[2]	[2]	[2]	[2]⁺
图像
对偶图像

面的组成

四角化菱形十二面体由48个全等的不等边三角形组成^[21]。

该三角形三边皆不等长。若其对偶多面体的大斜方截半立方体边长为单位长，则对应的四角化菱形十二面体组成面，最短边长为 ${\tfrac {2{\sqrt {3\left(10-{\sqrt {2}}\right)}}}{7}}$ 、次长边长为 ${\tfrac {3{\sqrt {6\left(2+{\sqrt {2}}\right)}}}{7}}$ 、最长边长为 ${\tfrac {2{\sqrt {6\left(10+{\sqrt {2}}\right)}}}{7}}$ ^[15]。若最短边长为单位长，则对应的短边长为1、次长边长为 ${\tfrac {3{\sqrt {2{\sqrt {2}}+4}}}{2{\sqrt {-{\sqrt {2}}+10}}}}\approx 1.338$ 、最长边长为 ${\tfrac {\sqrt {2{\sqrt {2}}+20}}{\sqrt {-{\sqrt {2}}+10}}}\approx 1.631$ ，三个角角度分别为(55.02° ,37.77° ,87.20°)^[22]。