基爾霍夫電路定律

基爾霍夫電路定律(Kirchhoff Circuit Laws)簡稱為基爾霍夫定律,指的是兩條電路學定律,基爾霍夫電流定律與基爾霍夫電壓定律。它們涉及了電荷的守恆及電勢的保守性。1845年,古斯塔夫·基爾霍夫首先提出基爾霍夫電路定律。現在,這定律被廣泛地應用於電機工程學。
從馬克士威方程組可以推導出基爾霍夫電路定律。但是,基爾霍夫並不是依循這條思路發展,而是從格奧爾格·歐姆的工作成果加以推廣得之。
基爾霍夫電流定律[编辑]

基爾霍夫電流定律又稱為基爾霍夫第一定律,表明[1]:
所有進入某節點的電流的總和等於所有離開這節點的電流的總和。
或者,更詳細描述,
假設進入某節點的電流為正值,離開這節點的電流為負值,則所有涉及這節點的電流的代數和等於零。
以方程式表達,對於電路的任意節點,
- ;
其中, 是第 個進入或離開這節點的電流,是流過與這節點相連接的第 個支路的電流,可以是實數或複數。
由於累積的電荷(單位為庫侖)是電流(單位為安培)與時間(單位為秒)的乘積,從電荷守恆定律可以推導出這條定律。其实质是稳恒电流的连续性方程,即根据电荷守恒定律,流向节点的电流之和等于流出节点的电流之和。[2]
導引[编辑]
思考電路的某節點,跟這節點相連接有 個支路。假設進入這節點的電流為正值,離開這節點的電流為負值,則經過這節點的總電流 等於流過支路 的電流 的代數和:
- 。
將這方程式積分於時間,可以得到累積於這節點的電荷的方程式:
- ;
其中, 是累積於這節點的總電荷, 是流過支路 的電荷, 是檢驗時間, 是積分時間變數。
假設 ,則正電荷會累積於節點;否則,負電荷會累積於節點。根據電荷守恆定律, 是個常數,不能夠隨著時間演進而改變。由於這節點是個導體,不能儲存任何電荷。所以, 、 ,基爾霍夫電流定律成立:
- 。
含時電荷密度[编辑]
從上述推導可以看到,只有當電荷量為常數時,基爾霍夫電流定律才會成立。通常,這不是個問題,因為靜電力相斥作用,會阻止任何正電荷或負電荷隨時間演進而累積於節點,大多時候,節點的淨電荷是零。
不過,電容器的兩塊導板可能會允許正電荷或負電荷的累積。這是因為電容器的兩塊導板之間的空隙,會阻止分別累積於兩塊導板的異性電荷相遇,從而互相抵消。對於這狀況,流向其中任何一塊導板的電流總和等於電荷累積的速率,而不是零。但是,若將位移電流 納入考慮,則基爾霍夫電流定律依然有效。詳盡細節,請參閱條目位移電流。只有當應用基爾霍夫電流定律於電容器內部的導板時,才需要這樣思考。若應用於電路分析(circuit analysis)時,電容器可以視為一個整體元件,淨電荷是零,所以原先的電流定律仍適用。
由更技術性的層面來說,取散度於馬克士威修正的安培定律,然後與高斯定律相結合,即可得到基爾霍夫電流定律:
- ;
這是電荷守恆的微分方程式。以積分的形式表述,從封閉表面流出的電流等於在這封閉表面內部的電荷 的流失率:
- 。
基爾霍夫電流定律等價於電流的散度是零的論述。對於不含時電荷密度 ,這定律成立。對於含時電荷密度,則必需將位移電流納入考慮。
應用[编辑]
以矩陣表達的基爾霍夫電流定律是眾多電路模擬軟件(electronic circuit simulation)的理論基礎,例如,SPICE或NI Multisim。
基爾霍夫電壓定律[编辑]
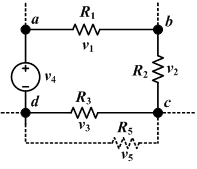
基爾霍夫電壓定律又稱為基爾霍夫第二定律,表明[1]:
沿著閉合迴路所有元件兩端的電勢差(電壓)的代數和等於零。
或者,換句話說,
沿著閉合迴路的所有電動勢的代數和等於所有電壓降的代數和。
以方程式表達,對於電路的任意閉合迴路,
- ;
其中, 是這閉合迴路的元件數目, 是元件兩端的電壓,可以是實數或複數。
基尔霍夫电压定律不仅应用于闭合回路,也可以把它推广应用于回路的部分电路。[需要解释]
電場與電勢[编辑]
- ;
其中, 是電勢, 是電場, 是從參考位置到位置 的路徑, 是這路徑的微小線元素。
那麼,基爾霍夫電壓定律可以等價表達為:
- ;
其中, 是積分的閉合迴路。
這方程式乃是法拉第電磁感應定律對於一個特殊狀況的簡化版本。假設通過閉合迴路 的磁通量為常數,則這方程式成立。
這方程式指明,電場沿著閉合迴路 的線積分為零。將這線積分切割為幾段支路,就可以分別計算每一段支路的電壓。
理論限制[编辑]
由於含時電流會產生含時磁場,通過閉合迴路 的磁通量是時間的函數,根據法拉第電磁感應定律,會有電動勢 出現於閉合迴路 。所以,電場沿著閉合迴路 的線積分不等於零。這是因為電流會將能量傳遞給磁場;反之亦然,磁場亦會將能量傳遞給電流。
對於含有電感器的電路,必需將基爾霍夫電壓定律加以修正。由於含時電流的作用,電路的每一個電感器都會產生對應的電動勢 。必需將這電動勢納入基爾霍夫電壓定律,才能求得正確答案。
頻域[编辑]
思考單頻率交流電路的任意節點,應用基爾霍夫電流定律
- ;
其中, 是第 個進入或離開這節點的電流, 是其振幅, 是其相位, 是角頻率, 是時間。
對於任意時間,這方程式成立。所以,設定相量 ,則可以得到頻域的基爾霍夫電流定律,以方程式表達,
- 。
頻域的基爾霍夫電流定律表明:
所有進入或離開節點的電流相量的代數和等於零。
這是節點分析的基礎定律。
類似地,對於交流電路的任意閉合迴路,頻域的基爾霍夫電壓定律表明:
沿著閉合迴路所有元件兩端的電壓相量的代數和等於零。
以方程式表達,
- ;
其中, 是閉合迴路的元件兩端的電壓相量。
這是網目分析(mesh analysis)的基礎定律。
參見[编辑]
| ||||||||||||||||||||||
參考[编辑]
- ^ 1.0 1.1 Alexander, Charles; Sadiku, Matthew, Fundamentals of Electric Circuits 3, revised, McGraw-Hill: pp. 37–43, 2006, ISBN 9780073301150
- ^ 普通物理学(修订版)(化学数学专业用).汪昭义 主编.华东师范大学出版社.P320.9.3 基尔霍夫定律.ISBN 978-8-5617-0444-8
- Paul, Clayton R. Fundamentals of Electric Circuit Analysis. John Wiley & Sons. 2001. ISBN 978-0-471-37195-3.
- Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers (6th ed.). Brooks/Cole. 2004. ISBN 978-0-534-40842-8.
- Tipler, Paul. Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. 2004. ISBN 978-0-7167-0810-0.
外部連結[编辑]
- 麻省理工學院電機工程系視聽教學:基爾霍夫定律 (页面存档备份,存于互联网档案馆)。
- 國立交通大學物理系視聽教學:電子學[永久失效連結]。
- Kirchhoff's circuit laws on Khan Academy
| ||||||||||||||||||||||||||||||||||














































