星形八面体[编辑]
外观
 | ||||||||||||
| 类别 | 复合正多面体 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 对偶多面体 | 二复合正四面体 | |||||||||||
| 识别 | ||||||||||||
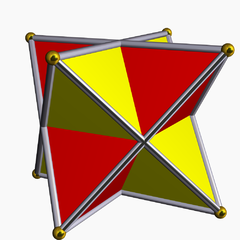
| 名称 | 星形八面体 | |||||||||||
| 参考索引 | W19 | |||||||||||
| 数学表示法 | ||||||||||||
| 考克斯特符号 | {4,3}[2{3,3}]{3,4}[1] | |||||||||||
| 施莱夫利符号 | {{3,3}} a{4,3} ß{2,4} ßr{2,2} | |||||||||||
| 性质 | ||||||||||||
| 体 | 2 | |||||||||||
| 面 | 8 | |||||||||||
| 边 | 12 | |||||||||||
| 顶点 | 8 | |||||||||||
| 欧拉特征数 | F=8, E=12, V=8 (χ=4) | |||||||||||
| 组成与布局 | ||||||||||||
| 复合几何体数量 | 2 | |||||||||||
| 复合几何体种类 | 2个正四面体 | |||||||||||
| 面的种类 | 8个正三角形 | |||||||||||
| 对称性 | ||||||||||||
| 对称群 | chiral octahedral (Oh) | |||||||||||
| 旋转对称群 | chiral tetrahedral (Td) | |||||||||||
| 图像 | ||||||||||||
| ||||||||||||
在几何学中,星形八面体(英语:Stellated octahedron)是八面体中唯一的星形多面体,是一种二复合四面体,又称为八角星体(英语:stella octangula、拉丁语为eight-pointed star,意为八角星[注 1]),在1609时由约翰内斯·开普勒命名,然而他是位早期的几何学家。事实上,早在1509年,卢卡·帕西奥利已经在其作品神曲中描绘了此种多面体[2]。
历史
[编辑]1509年,卢卡·帕西奥利首先描述了该复合体,并将其在作品神曲中描绘[2]。1609年约翰内斯·开普勒将其命名。埃德蒙·赫斯在1876年将其与其他复合体一同描述、提出。1974年,马格努斯·J·温尼尔将星形八面体归类在温尼尔多面体模型中并给予编号W19,并记录于《多面体模型》中[3]。
复合多面体
[编辑]在几何学中,星形八面体又被称为二复合四面体,是一种凹多面体,属于星形多面体,外观看起来像两个正四面体卡在一起。这可以被看作是多面体和星形多面体的复合体,由两个正四面体构成,由于正四面体属于自身对偶多面体,因此组合成的星形八面体的对偶多面体也是自己。
正八面体的星形仅有一种,即是上述由两个正四面体构成的星形八面体。此外,此多面体也可以看做是一个三角化的八面体,但与卡塔兰立体中的三角化八面体不同。
它可以由安排在对称群为八面体旋转对称(Oh)的的几何结构中。
结构
[编辑]星形八面体可以用几种方式构成:
 立体图 |
 星状平面 |
星状图是正八面体,以黄色星状平面表示 |
- 也可以将两个正四面体交错卡在一起构成(一个正四面体和它的对偶四面体构成)
- 也可借由正八面体透过Kleetope变换构成,即在正八面体的每个面上加入角锥。这种结构与卡塔兰立体中的三角化八面体有著相同的拓朴结构。
- 它与是立方体的所有割面共用相同的顶点排布。
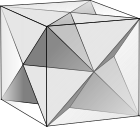 立方体的所有三角形割面可构成星形八面体 |
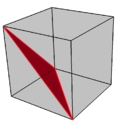 立方体的其中一个三角形割面以红色表示 |
文化
[编辑]- 角色扮演游戏《Fate/Grand Order》中的圣晶石。
- VOCALOID 4声库“星尘”手上托着的小星星是星形八面体形状。
- 奇迹暖暖“云空之境”活动的羁绊之辰[4]。
参见
[编辑]注释
[编辑]参考文献
[编辑]- ^ Regular polytopes, pp.48-50, p.98
- ^ 跳转到: 2.0 2.1 Barnes, John, Shapes and Solids, Gems of Geometry, Springer: 25–56, 2009, ISBN 978-3-642-05091-6, doi:10.1007/978-3-642-05092-3_2.
- ^ Wenninger, Magnus. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
- ^ 《奇迹暖暖》云空之境活动规则详解 活动玩法技巧分享. [2019-01-25]. (原始内容存档于2020-03-16).
- Coxeter, HSM, Regular Polytopes, 3rd Edn., Dover 1973.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. The Fifty-Nine Icosahedra 3rd. Tarquin. 1999. ISBN 978-1-899618-32-3. MR 0676126. (1st Edn University of Toronto (1938))
- 埃里克·韦斯坦因. Tetrahedron 5-Compound. MathWorld.
- Metal Sculpture of Five Tetrahedra Compound (页面存档备份,存于互联网档案馆)
- VRML model: [1]
- Compounds of 5 and 10 Tetrahedra (页面存档备份,存于互联网档案馆) by Sándor Kabai, The Wolfram Demonstrations Project.
延伸阅读
[编辑]- Wenninger, Magnus. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
外部链接
[编辑]- 埃里克·韦斯坦因. Stella Octangula. MathWorld.
- 埃里克·韦斯坦因. Compound of two tetrahedra. MathWorld.
- Klitzing, Richard. 3D compound. bendwavy.org.



