電荷
在電磁學裡,電荷(英語:electric charge)是構成物質的基本粒子的一種物理性質,原子中的質子和電子分別帶有正電荷和負電荷,而中子不帶電荷。[1]帶有電荷的物質稱為帶電物質,帶有電荷的粒子稱為帶電粒子。兩個帶電粒子之間會互相施加作用力,電荷符號相同的粒子會相互排斥,電荷符號不同的粒子會相互吸引,該作用力可由庫侖定律得出。
電荷是許多次原子粒子所擁有的一種基本守恆性質。電荷決定了帶電粒子在電磁方面的物理行為。靜止的帶電粒子會產生電場,移動中的帶電粒子會產生電磁場,帶電粒子也會被電磁場所影響。一個帶電粒子與電磁場之間的相互作用稱為電磁力或電磁交互作用。這是四種基本交互作用中的一種。
物體所帶過剩電荷的總量稱為電荷量,簡稱電荷或電量。[1]電荷量的國際單位是庫侖(C),通常用符號Q表示。一個質子攜帶的電荷量稱為基本電荷,約為1.602× 10-19庫侖,用符號 表示,一個電子攜帶的電荷量為 。夸克攜帶的電荷量為e/3的倍數。
研究帶電粒子相互作用的經典學術領域稱為經典電動力學。假若量子效應可以被忽略,則經典電動力學能夠很正確地描述出帶電物質在電磁方面的物理行為。研究帶電粒子與它們之間由光子媒介的相互作用的學術領域稱為量子電動力學。
歷史
[編輯]西元前600年左右,希臘的哲學家泰勒斯記錄,琥珀摩擦貓毛以後會吸引像羽毛一類的輕微物體,假若摩擦時間夠久,甚至會有火花出現[2]。

1600年,英國醫生威廉·吉爾伯特,對於電磁現象做了一個很仔細的研究。他指出琥珀並非唯一經過摩擦時會產生靜電的物質,並且區分出電與磁不同的屬性[3]。他撰寫了第一本闡述電和磁的科學著作《論磁石》。吉爾伯特創建了新拉丁語的術語「electrica」(源自於「ήλεκτρον」,「ēlektron」,希臘文的「琥珀」),英文翻譯為「electrics」,意指如同琥珀一般當摩擦後會吸引微小物體的物質[4]。這新拉丁術語後來給出了英文術語「electricity」,最先出現於1646年,湯瑪斯·布朗(Thomas Browne)的著作《Pseudodoxia Epidemica》(英文書名《Enquries into very many received tenets and commonly presumed truths》)[5]。隨後,於1660年,科學家奧托·馮·格里克發明了可能是史上第一部靜電發電機(electrostatic generator)。他將一個硫磺球固定於一根鐵軸的一端,然後一邊旋轉硫磺球,一邊用干手摩擦硫磺球,使硫磺球產生電荷,能夠吸引微小物質[6]。
史蒂芬·戈瑞於1729年發現了電傳導,即電荷可以從一個物質傳導至另外一個物質的性質。只有某些種類的物質會傳導電荷,其中,金屬的能力最為優良。從此,科學家不再認為產生電荷的物體與所產生的電荷是不可分離的,而認為電荷是一種獨立存在的物質,在那時被稱為「電流體」。[7]1733年,查爾斯·篤費做實驗發現,假若被絲綢摩擦後的玻璃對於帶電的金葉片呈現出排斥的現象,則被羊毛摩擦後的琥珀會對這帶電的金葉片呈現出吸引的現象,因此,他將電分為兩種,被絲綢摩擦後的玻璃帶有「玻璃電」,而被羊毛摩擦後的琥珀則帶有「樹脂電」。[4]:484-5這兩種電會彼此相互抵銷。這理論稱為「雙流體理論」,是對於電現象首次給出解釋的電學理論。[8]:20稍後,美國科學家埃柏奈澤·肯納斯理也獨立獲得相同的結論。[9]:118
在十八世紀,美國人班傑明·富蘭克林是電學最前端的專家之一,他認為「單流體理論」比較正確。他想像電儲存於所有物質裡,並且通常處於平衡狀態,而摩擦動作會使得電從一個物體流動至另一個物體。例如,他認為累積的電是儲存於萊頓瓶的玻璃,用絲巾摩擦玻璃使得電從絲巾流動至玻璃。這流動形成了電流。他建議電量低於平衡的物體載有負電量,電量高於平衡的物體載有正電量。他任意地設定玻璃電為正電,具有多餘的電;而琥珀電為負電,缺乏足夠的電。同時期,英國學者威廉·沃森也獨立達到同樣的結論。1747年,富蘭克林假定在一個孤立系統內,總電荷量恆定,這稱為電荷守恆定律。[7]:43-47[10]:1112
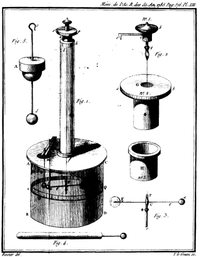
1785年,使用查爾斯·庫侖與約翰·米歇爾分別獨立發明的扭秤,庫侖證實了約瑟夫·普利斯特里的基本定律:帶有靜態電荷的兩個物體彼此之間所感受的作用力與距離成平方反比。這奠定了靜電的基本定律。[7]:56
劍橋大學卡文迪許實驗室的約瑟夫·湯姆孫於1897年實驗計算出組成陰極射線的粒子的電荷質量比。由於這數值與陰極物質、放電管內氣體無關,湯姆孫推斷,陰極射線的粒子源自於在陰極附近被強電場分解的氣體原子,這粒子為所有物質的組分。由於湯姆孫獲得的電荷質量比是電解實驗獲得的氫離子電荷質量比的千分之一倍,湯姆孫錯誤推斷,這粒子的質量很小,電荷很大,稍後他又修正為,粒子的帶電量等於電解單位電荷,而質量則為氫原子的千分之一。湯姆孫稱這粒子為「微粒」(corpuscle),就是微小粒子的意思,但學術界後來採用術語「電子」來標記這粒子。[11]1899年,湯姆孫實驗團隊做光電效應實驗與熱離子發射實驗測得於先前陰極射線等同的電荷質量比,這意味著這些實驗所涉及的粒子都是電子。[12]:23。由於湯姆孫建議電子為組成物質的基礎粒子,並且做實驗確切證實他的論述,他被公認為電子的發現者。電子是人類發現的第一種基礎粒子。[13]:40-43
1898年,湯姆孫做實驗發現,假設照射X射線於氣體,使用所產生的負離子來將過飽和水蒸氣凝結,則可以粗略測量帶電水滴的帶電量,其與電解實驗獲得的氫離子帶電量大約相等。隔年,他利用光電效應來進行類似實驗,仍舊獲得同樣結果。但是這些實驗所獲得的數值是很多帶電水滴的統計平均值,它們並未能證實所有電子的帶電量相等。美國物理學家羅伯特·密立根在1909年起完成一系列實驗測量電子的帶電量。起初,他使用水滴為測量對象,後來,由於油滴的蒸發率較低,他改使用油滴,[12]:23, 61在這些油滴實驗裏,他仔細地測量,帶電油滴在重力與電場的庫倫力的雙重影響下的懸浮運動。從獲得的數據,所有油滴的帶電量皆為同一數字的整倍數,因此認定此數值為單一電子的電荷,即基本電荷,並且斷定,電的基本結構是自然不可分的基本電荷,而不是多個不同數值的統計平均值。[14]:196-197俄國物理學者亞伯蘭·約費於1911年利用光電效應,照射紫外線於鋅金屬微粒子來製成帶電金屬微粒子,然後測量其帶電量,他也獨立獲得同樣結果。[15]
靜電
[編輯]假設在平衡狀況,某物體的總電量不等於零,也就是說,這物體帶有正電荷或負電荷,則稱此物體帶有靜電。這方面的問題屬於靜電學領域。琥珀在經過用貓毛摩擦後,能夠吸引輕小物體,這現象稱為靜電現象。這是負電荷從貓毛轉移到琥珀後,所呈現的電性。當兩個處於電勢不相等的物體相互接觸在一起,就會發生另外一種靜電現象,稱為靜電放電,使得一個物體的電荷流動至另一個物體,從而促成電勢相等。雷電是一種比較劇烈的靜電放電現象。在大自然中,因為雲層累積的正負電荷劇烈中和,會產生雷電和其所伴隨的電光、雷聲、熱量。
點電荷
[編輯]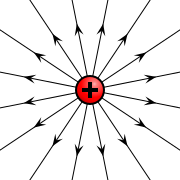

帶電粒子時常被稱為電荷,但電荷本身並非粒子,只是為了方便描述,可以將它想像成粒子。帶電量多者稱為具有較多電荷。處於一外電場的帶電粒子,其所感受到的外電場的庫侖力相依於其帶電量。
點電荷是帶電粒子的理想模型。真正的點電荷並不存在,只有當帶電粒子之間的距離超大於粒子的尺寸,或是帶電粒子的形狀與大小對於彼此相互施加的作用力的影響能夠被忽略時,可稱此帶電體為「點電荷」。
一個實際帶電體能否視為點電荷,不僅與帶電體本身有關,還取決於問題的性質和精確度的要求。點電荷是建立基本規律時必要的抽象概念,也是分析複雜問題時不可少的分析手段。例如,庫侖定律、勞侖茲力定律的建立,帶電體所產生的電場以及幾個帶電體之間彼此相互作用的定量研究,試驗電荷的引入等等,都應用了點電荷的觀念。
庫侖定律
[編輯]給予兩個電量分別為、,位置分別為、的點電荷。根據庫侖定律,點電荷作用於點電荷的力量的大小與方向,以方程式表達為
- 。
假若兩個點電荷同性(電荷的正負號相同),則其電量的乘積是正值,兩個點電荷互相排斥。反之,假若兩個點電荷異性(電荷的正負號相反),則其電量的乘積是負值,兩個點電荷互相吸引。
束縛電荷與自由電荷
[編輯]有時候,雖然物體的總電量等於零,電荷分布可能會不均勻(例如,因為存在着外電場)。對於這狀況,這物質稱為電極化物質。束縛電荷是由於電極化而出現的電荷,束縛於原子內部。與束縛電荷明顯不同,自由電荷是從外部置入的額外的電荷,不被束縛於原子內部。帶電粒子朝着某方向的運動形成了電流,特別是在金屬內部運動的電子。
粒子的電荷
[編輯]在粒子物理學中,許多粒子都帶有電荷。電荷在粒子物理學中是一個相加性量子數,電荷守恆定律也適用於粒子,反應前粒子的電荷之和等於反應後粒子的電荷之和,這對於強相互作用、弱相互作用、電磁相互作用都是嚴格成立的。
反粒子帶有的電荷與對應粒子帶有的電荷,電量相同,電性相異。夸克帶有非整數電荷,不是-e/3,就是2e/3;但是科學家從未觀察到單獨夸克的存在(這事實可以用漸近自由(Asymptotic freedom)的理論來解釋)。
電荷宇稱時間對稱
[編輯]電荷宇稱時間對稱(CPT-symmetry)對於粒子和反粒子的相對特性設下了強烈的約束。因此,可以嚴格地測試這理論。例如,質子和反質子的電荷的總和必須正好等於零。這全等式的精確度已經作實驗測試至108分之一。使用潘寧阱(Penning trap)來囚禁反質子,質子和反質子的電荷質量比相等性質的精確度也被測試至6×109分之一[16]。
電荷守恆
[編輯]電荷守恆定律表明,在一個孤立系統裏,不論發生什麼變化,總電荷必定保持不變。所有物理程序都必須遵守這定律。在量子力學里,從波函數的規範不變性可以推導出這定律。
流入某體積的淨電流為
- ;
其中,是電流,是電流密度,是包圍體積的閉曲面,是微小面向量元素,垂直於從體積內朝外指出。
應用散度定理,將這方程式寫為
- 。
總電荷量與體積內的電荷密度的關係為
- 。
電荷守恆要求,流入體積的淨電流,等於體積內總電荷量的變率:
- 。
所以,
- 。
對於任意體積,上述方程式都成立。所以,可以將被積式提取出來:[17]
- 。
注釋
[編輯]參考文獻
[編輯]- ^ 1.0 1.1 《物理学》网络课程(第三版). phy.sdu.edu.cn. [26 August 2023]. (原始內容存檔於2023-08-25).
- ^ Stewart, Joseph, Intermediate Electromagnetic Theory, World Scientific: pp. 50, 2001, ISBN 9-8102-4471-1
- ^ Simpson, Brian, Electrical Stimulation and the Relief of Pain, Elsevier Health Sciences: pp. 5–6, 2003, ISBN 0-4445-1258-6
- ^ 4.0 4.1 Benjamin, Park, A history of electricity (The intellectual rise in electricity) from antiquity to the days of Benjamin Franklin, New York: J. Wiley: 315, 1898, ISBN 978-1313106054
- ^ Chalmers, Gordon, The Lodestone and the Understanding of Matter in Seventeenth Century England, Philosophy of Science, 1937, 4 (1): pp. 75–95, doi:10.1086/286445
- ^ Williams, Henry, A History of science, Volume 2, Harper: 170, [1904], ISBN 978-1151497598
- ^ 7.0 7.1 7.2 Whittaker, ET, A history of the theories of aether and electricity. Vol 1, Nelson, London: pp. 37–44, 56, 1951
- ^ Keithley, J.F. The Story of Electrical and Magnetic Measurements: From 500 B.C. to the 1940s. IEEE Press. 1999. ISBN 0-7803-1193-0.
- ^ Florian Cajori. A History of Physics in Its Elementary Branches: Including the Evolution of Physical Laboratories. Macmillan. 1917.
- ^ Ford, Guy (編), Compton’s Pictured Encyclopedia, Vol 3, F. E. Compton, 1922
- ^ Corpuscle. Marriam-Webster, Inc. [2019-05-23]. (原始內容存檔於2019-05-06).
a minute particle
- ^ 12.0 12.1 Buchwald, J.Z.; Warwick, A. Histories of the Electron: The Birth of Microphysics. MIT Press. 2001. ISBN 978-0-262-52424-7.
- ^ Kragh, Helge. Quantum Generations: A History of Physics in the Twentieth Century Reprint. Princeton University Press. 2002. ISBN 978-0691095523.
- ^ Greenberger, D.; Hentschel, K.; Weinert, F. (編), Compendium of Quantum Physics: Concepts, Experiments, History and Philosophy 2009th Edition, Springer, 2009, ISBN 978-3540706229
- ^ Mikerov, Alexander, From history of electrical engineering V: Electron discovery and its properties estimation, St. Petersburg, Russia: IEEE, 2016, doi:10.1109/EIConRusNW.2016.7448102
|book-title=被忽略 (幫助) - ^ G. Gabrielse, Antiproton mass measurements, International Journal of Mass Spectrometry, 2006, 251 (2–3): 273–280, doi:10.1016/j.ijms.2006.02.013
- ^ Griffiths, David J., Introduction to Electrodynamics (3rd ed.), Prentice Hall: pp. xiv, 213, 1998, ISBN 0-13-805326-X
























