跳至內容

視差

維基百科，自由的百科全書
  此條目介紹的是從不同位置觀察同一物體時的明顯位移。關於其他用法，請見「視差 (消歧義)」。
由於觀察點的改變，一個物體相對於遠方背景的移動，顯示視差的簡化插圖。當從"A點"觀察時，該物體顯示在藍色方格的前面。當從"B點"觀察時，顯示該物體移動到紅色方格的前面
這是視差的動畫示例。隨着觀測點從一測移至另一側，遠方物體的移動比接近相機的物體緩慢

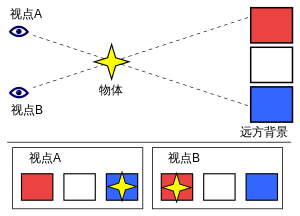
視差（英語：parallax，來自古希臘語 παράλλαξις（parallaxis），意即：「差異」）是指從兩個不同位置觀察同一個物體時，此物體在視野中的位置變化與差異[1][2]。從兩個觀察點看目標，兩條視線之間的夾角叫做這兩個點的視差角，兩點之間的距離稱作視差基線。

從同樣的兩個觀察點看，目標物體距離越近就有越大的視差，因此視差可以被用來反向估算物體的距離。比如天文學家使用視差的原理測量天體距離地球的距離，包括月球、太陽和在太陽系之外的恆星。例如，依巴谷衛星測量了超過100,000顆鄰近恆星的距離。這為天文學提供了測量宇宙距離尺度的階梯，是其它測距方法的基礎。在此處，"視差"這個名詞是兩條到恆星的視線交角的角度或半角度。

一些光學儀器，像是雙筒望遠鏡、顯微鏡、和雙反相機，會以略為不同的角度觀看物體，都會受到視差的影響。許多動物的兩隻眼睛有着重疊的視野，可以利用視差獲得深度知覺；此一過程稱為立體視覺。這種效果在電腦視覺用於電腦立體視覺，並有一種裝置稱為視差測距儀，利用它來測量發現目標的距離，也可以改變為測量目標的高度。

一個簡單的，日常都能見到的視差例子是，汽車儀錶板上"指針"顯示的速度計。當從正前方觀看時，顯示的正確數值可能是60；但從乘客的位置觀看，由於視角的不同，指針顯示的速度可能會略有不同。

視知覺

[編輯]
主條目：立體視覺、深度知覺、雙眼視覺和雙眼像差
這張圖像演示視差。太陽位於路燈的上方，太陽和路燈在水中的倒影是虛像。虛像的位置是在水面的下方，提供了一個不同的點瞭望路燈，顯示出相對於太陽的位置有了改變。

如同人類和其他動物的雙眼都在頭上不同的位置，它們提供了不同的觀點。這是立體視覺的基礎，在這個過程中，大腦接收了不同的訊息，從而獲得深度知覺，並從兩眼的視差估計到物體的距離[3]。有些動物會利用運動視差，這些動物依靠移動（也許只是頭部）來獲得不同的觀點。例如，鴿子（它們兩眼的視場沒有重疊，因此沒有立體視覺）上下擺動頭部以獲得深度[4]。

視差的應用

[編輯]

視差在應用上根據不同需要派生出各個稍有不同的概念：

  • 物理學中，指在不同位置觀察遠近兩物體時，它們間發生相對位置變化的現象。
  • 天文學中，指因為觀測者位置的移動或由不同地點觀測同一天體而引起的方向變化；測量天體視差是確定天體之間距離最基本的方法。天文學家在早期使用此方法測量了月球（從紐約和華盛頓拍攝的照片分析）離地球的距離與天鵝座61的距離。
  • 攝影測量中，指立體像對上同名像點的坐標差，其橫坐標差稱為「左右視差」，縱坐標差稱為「上下視差」；在航空攝影測量中，左右視差可以推算地面點之間的高差，上下視差可用以確定像片之間在攝影時的相對關係。
  • 攝影術中，指從相機取景器中看到的物體位置和鏡頭攝入的物體位置不相一致的現象；相機距物體越遠，視差越小；高級取景器有校正視差的機能，使物體在感光成像上的位置和從取景器中所看到的位置無論遠近都相合；單鏡反光機由於取景器和攝影通過同一物鏡，所以基本沒有視差。

天文學的距離測量

[編輯]

恆星視差

[編輯]
主條目：恆星視差

在星際的尺度，視差的創建來自地球在軌道上不同的位置導致鄰近的恆星相對於遙遠天體的移動。通過觀測視差，測量角度和使用幾何學，可以確定到不同天體的距離。當被討論的天體是恆星時，這種效應稱為恆星視差。

恆星視差最常被使用的是周年視差，定義是從地球和太陽觀察恆星的視角差，也就是以地球繞太陽的平均軌道半徑看一顆恆星在對角的角度。1秒差距（3.26光年）被定義為周年視差為1角秒的距離。周年視差一般是通過觀察恆星在年的不同時間，隨着地球在它的軌道上移動測量的。周年視差是第一個最可靠的測量最接近恆星的方法。第一個成功測量到的恆星視差是白塞耳在1833年使用量日儀測量的天鵝座61[5]。恆星視差依然是校準其他測量方法的標準。精確測量距離的基礎是恆星視差，它需要測量地球到太陽的距離，而現在是以雷達在行星表面的反射來測量[6]。

在這些計算中所涉及的角度都很小，因此很難測量。距離太陽最近的恆星（因此這顆恆星有最大的視差），比鄰星，周年視差是0.7687±0.0003角秒[7]。這相當於從5.3公里之外觀察直徑2公分大小物體的弦所形成的角。

恆星視差是如此的小，因此在無法觀測到恆星視差的年代，「恆星視差不存在」被作為反對日心說的主要科學論證。很明顯的，如果星星的距離夠遠，從歐幾里得的幾何學是無法察覺的，但由於種種的原因，使這種巨大的距離難以置信：其中之一是為了使缺乏視差的恆星能夠相容，土星軌道和第八領域（恆星）之間必須有巨大而不太可能存在的空隙，使得第谷成為哥白尼日心說的主要反對者[8]。

在1989年，依巴谷衛星發射的主要目的就是觀察近距離恆星的視差和自行，這種方法使數量增加了10倍。即便如此，依巴谷衛星能測量出視差角的恆星距離也只能達到1,600光年，相較於銀河系的直徑只比1%多了一點。歐洲太空總署的蓋亞任務，預計在2012年升空，在2013年上線，能夠讓視差角的測量精確度達到10微秒，將能夠繪製出鄰近地球數萬光年內恆星（與潛在行星）的位置圖[9]。

演算法

[編輯]
恆星視差運動

以視差來測量距離在三角學的原則上是一種特殊狀況，如果要解出在網絡中三角形所有的邊和角，除了網絡中所有的角，至少有一邊的長度必須被測量。因此，仔細測量過長度的一條基線可以解決整個三角網的規模。對視差而言，這個三角形是極其細長和狹窄的，測量的是最短的邊（觀測者的移動）和非常小的角（永遠都小於1角秒[5]，其餘的兩個角都接近90度），要測量的是長邊（實際上這兩邊的長是相同）。

假設這個角度很小（見下文的#推導），一個天體的距離（以秒差距量度）是視差（以角秒量度）的倒數：。例如，比鄰星的距離是1/0.7687=1.3009秒差距（4.243光年）[7]。

周日視差

[編輯]

周日視差是由地球自轉或在地球上不同地點觀察產生的視差。從地球上不同的地點觀測（在給定的同一時刻），月球和較小的類地行星或小行星會出現在背景天恆星上的位置會有所不同[10][11]。

月球視差

[編輯]

月球視差（通常是月球地平視差或月球赤道地平視差的縮寫），是（周日）視差的一個特殊例子：月球，是最靠近地球的天體，擁有迄今所有天體中最大的視差，可以超過1度[12]。

只要將恆星視差圖（上圖）的右下略加修改，就可以很好的說明月球視差。將假想的近端星改成月球，底部代表地球繞太陽的圓軌道改成地球的球體，圓圈是地球表面的一圈。然後，相對於背景恆星在位置角上的差異，就是從兩個不同位置看見的月球（地平）視差：在給定的時刻，從其中一個位置（就是圖中的垂直線），觀察到的月球正好在頭頂正上方，而另一個位置（從圖中的地球表面，大約就是修改前藍點的位置）觀測到的月球正好在地平線上。

月球（地平）視差可以定義為，以地球半徑為基線的月球對角[13]， 或者是如上被修改的縮小關係圖中的角度p。

任何時刻的月球地平視差取決於當時地球到月球的直線距離。由於月球繞地球的軌道如下所示大約是橢圓的軌道和攝動的影響，地月距離會不斷的改變。改變的範圍在線距離上是56至63.7地球半徑，相當於地平視差1度的大小，對應的弧度角是從約61.4』到約至54』[12]。在天文年曆和類似的出版品會以表格製作出每天固定時間的月球水平視差和/或線距離，方便天文學家（以前還有領航員），和以這種方法研究月球運動說（Lunar theory）伴隨着時間的座標變化。

周日月球視差關係圖

視差也可以用來確定到月球的距離。

從一個地點測量月球視差的方法是利用月食。完整的地球影子在月球上的視曲率半徑等於從月球到地球和太陽距離之間的差別。這個可以看見的半徑等於0.75度，從這兒（太陽的視半徑是0.25度）可以獲得地球的視半徑是1度。這將導出地月距離是60個地球半徑，或是384,000公里。阿里斯塔克斯是第一個使用這種方法的人[14]，之後的依巴谷和托勒密也發現這種方法並用於他們的工作中[15]。右圖顯示出在以地球為中心且沒有自轉的行星模型中，地心和靜地壓的行星系統周日月球視差。它還演示了很重要的一點，觀測者不需要運動也可以形成視差，反過來，一些所謂的視差定義，很可能純粹是由觀測者的運動造成的。

另一種方法是在地球上兩個不同的地點，在完全相同的時間很精確的擷取兩張月球位置的影像，比較相對於背景恆星的位置。使用地球的方位，測量這兩個點的方位，和這兩個點在地球上的距離，可以用三角學測量月球的距離：

月球視差的一個例子：月掩昴宿星團

這是儒勒·凡爾納在從地球到月球這本書中所提到的方法：

直到此刻，許多人仍然不知道如何計算地球與月球相隔的距離。他們的環境教導他們這個距離是通過視差的觀察和測量得到的。如果視差這個字令他們感到迷惑，他們被告知這是從地球半徑的兩端連接到月球的兩條直線的對角。如果他們懷疑這種方法的完備性，他們立刻可以看到的不只是地球到月球平均距離的數值，234,347英里（94,330leagues），並且誤差小於70英里（大約30leagues）。

太陽視差

[編輯]

在哥白尼提出日心系統之後，地球繞着太陽公轉，它可以建立起一個沒有正確尺寸的太陽系模型。若要確定尺寸，它只需要測量在太陽系內一個天體的距離，也就是說，地球到太陽的平均距離（現在稱為天文單位，或以AU表示）。當以三角測量發現，從地球中心和表面觀測太陽的位置差異，即以地球半徑為基線測量太陽的對頂角，這被稱為太陽視差。知道太陽視差和地球的平均半徑，就能夠測量天文單位。首先，這是在估計膨脹宇宙和可見宇宙大小的漫漫長路上的一小步[16]。

測量地球到月球距離最原始的方法是在阿里斯塔克斯的《太陽和月球的距離與大小》一書中提出。他注意到太陽、月球和地球在上弦和下弦會形成直角三角形（月球位於直角上）。然後，他估計出月球、地球和太陽的夾角是87°。使用正確的幾何學，但不正確的觀測資料，阿里斯塔克斯推論太陽的距離略低於月球距離的20倍。但是，這個角度的正確數值接近89° 50'，而太陽的實際距離比月球遠了約390倍[14]。他指出月球和太陽有着幾乎一樣的視角大小，因此它們的直徑和與地球的距離有着相同的比值。因此，他也估計太陽比月球大20倍左右；這一結論，儘管源於不正確的資料，但他的邏輯是正確的。他也明確的表示太陽大於地球，這可以支持日心說的模型。

測量金星凌日的時間以確定太陽視差

儘管阿里斯塔克斯以正確的幾何原理觀測視差，但因為觀測的不正確導致結果不正確，卻也成為估計太陽系大小的基準長達2,000年之久，直到1761年和1769年觀測金星凌日後才被改正[14]。這個方法是愛德蒙·哈雷在1716年提出來的，可惜他未能活着看見結果。使用金星凌日的方法由於黑滴現象的影響而不太成功，但由此得到的結果是15,300萬公里，與目前接受的14,960萬公里，只有2%的差異。

相關條目

[編輯]

參考資料

[編輯]
  1. ^ Shorter Oxford English Dictionary. 1968. Mutual inclination of two lines meeting in an angle 
  2. ^ Parallax. Oxford English Dictionary Second Edition. 1989. Astron. Apparent displacement, or difference in the apparent position, of an object, caused by actual change (or difference) of position of the point of observation; spec. the angular amount of such displacement or difference of position, being the angle contained between the two straight lines drawn to the object from the two different points of view, and constituting a measure of the distance of the object. 
  3. ^ Steinman, Scott B.; Garzia, Ralph Philip. Foundations of Binocular Vision: A Clinical perspective. McGraw-Hill Professional. 2000: 2–5. ISBN 0-8385-2670-5. 
  4. ^ Steinman & Garzia 2000，p. 180.
  5. ^ 5.0 5.1 Zeilik & Gregory 1998，p. 44.
  6. ^ Zeilik & Gregory 1998，§ 22-3.
  7. ^ 7.0 7.1 Benedict, G. Fritz; McArthur, Barbara; Chappell, D. W.; Nelan, E.; Jefferys, W. H.; van Altena, W.; Lee, J.; Cornell, D.; Shelus, P. J.; Hemenway, P. D.; Franz, Otto G. Interferometric Astrometry of Proxima Centauri and Barnard's Star Using [ITAL]HUBBLE SPACE TELESCOPE[/ITAL] Fine Guidance Sensor 3: Detection Limits for Substellar Companions. The Astronomical Journal. 1999-08, 118 (2) [2022-10-13]. Bibcode:1999astro.ph..5318B. ISSN 1538-3881. arXiv:astro-ph/9905318 可免費查閱. doi:10.1086/300975. （原始內容存檔於2021-02-27）. 
  8. ^ See p.51 in The reception of Copernicus' heliocentric theory: proceedings of a symposium organized by the Nicolas Copernicus Committee of the International Union of the History and Philosophy of Science, Torun, Poland, 1973, ed. Jerzy Dobrzycki, International Union of the History and Philosophy of Science. Nicolas Copernicus Committee; ISBN 978-90-277-0311-8, ISBN 978-90-277-0311-8
  9. ^ Henney, Paul J. ESA's Gaia Mission to study stars. Astronomy Today. [2008-03-08]. （原始內容存檔於2008-03-17）. 
  10. ^ Seidelmann, P. Kenneth. Explanatory Supplement to the Astronomical Almanac. University Science Books. 2005: 123–125. ISBN 1891389459. 
  11. ^ Barbieri, Cesare. Fundamentals of astronomy. CRC Press. 2007: 132–135. ISBN 0750308869. 
  12. ^ 12.0 12.1 Astronomical Almanac e.g. for 1981, section D
  13. ^ Astronomical Almanac, e.g. for 1981: see Glossary; for formulae see Explanatory Supplement to the Astronomical Almanac, 1992, p.400
  14. ^ 14.0 14.1 14.2 Gutzwiller, Martin C. Moon-Earth-Sun: The oldest three-body problem. Reviews of Modern Physics. 1998-04-01, 70 (2). Bibcode:1998RvMP...70..589G. ISSN 0034-6861. doi:10.1103/RevModPhys.70.589 （英語）. 
  15. ^ Webb, Stephen, 3.2 Aristarchus, Hipparchus, and Ptolemy, Measuring the Universe: The Cosmological Distance Ladder, Springer: 27–35, 1999, ISBN 9781852331061 . See in particular p. 33: "Almost everything we know about Hipparchus comes down to us by way of Ptolemy."
  16. ^ Freedman, Wendy L. The Hubble constant and the expansion age of the Universe. Physics Reports. 2000-08,. 333-334 [2022-10-13]. Bibcode:2000PhR...333...13F. ISSN 0370-1573. arXiv:astro-ph/9909076 可免費查閱. doi:10.1016/S0370-1573(00)00013-2. （原始內容存檔於2022-10-24） （英語）. 

外部連結

[編輯]
取自 "https://zh.wikipedia.org/w/index.php?title=视差&oldid=82855416"