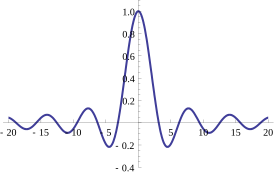
The characteristic function of a uniform U (–1,1) random variable. This function is real-valued because it corresponds to a random variable that is symmetric around the origin; however characteristic functions may generally be complex-valued. 在機率論 中,任何隨機變數 的特徵函數 (縮寫:ch.f,複數形式:ch.f's)完全定義了它的機率分布 。在實 直線上,它由以下公式給出,其中
X
{\displaystyle X}
φ
X
(
t
)
=
E
(
e
i
t
X
)
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{itX}\right)}
其中
t
{\displaystyle t}
實數 ,
i
{\displaystyle i}
虛數單位 ,
E
{\displaystyle E}
期望值 。
用動差母函數
M
X
(
t
)
{\displaystyle M_{X}(t)}
i
X
{\displaystyle iX}
X
{\displaystyle X}
φ
X
(
t
)
=
M
i
X
(
t
)
=
M
X
(
i
t
)
{\displaystyle \varphi _{X}(t)=M_{iX}(t)=M_{X}(it)}
與動差母函數不同,特徵函數總是存在。
如果
F
X
{\displaystyle F_{X}}
累積分布函數 ,那麼特徵函數由黎曼-斯蒂爾傑斯積分 給出:
E
(
e
i
t
X
)
=
∫
−
∞
∞
e
i
t
x
d
F
X
(
x
)
{\displaystyle \operatorname {E} \left(e^{itX}\right)=\int _{-\infty }^{\infty }e^{itx}\,dF_{X}(x)}
在機率密度函數
f
X
{\displaystyle f_{X}}
E
(
e
i
t
X
)
=
∫
−
∞
∞
e
i
t
x
f
X
(
x
)
d
x
{\displaystyle \operatorname {E} \left(e^{itX}\right)=\int _{-\infty }^{\infty }e^{itx}f_{X}(x)\,dx}
如果
X
{\displaystyle X}
向量 值隨機變數,我們便取自變數
t
{\displaystyle t}
t
X
{\displaystyle tX}
數量積 。
R
{\displaystyle R}
R
n
{\displaystyle R^{n}}
測度 的空間上對一個有界函數 進行積分,且對於每一個特徵函數都正好有一個機率分布。
一個對稱機率密度函數的特徵函數(也就是滿足
f
X
(
x
)
=
f
X
(
−
x
)
{\displaystyle f_{X}(x)=f_{X}(-x)}
x
>
0
{\displaystyle x>0}
x
<
0
{\displaystyle x<0}
勒維連續定理 說明,假設
(
X
n
)
n
=
1
∞
{\displaystyle (X_{n})_{n=1}^{\infty }}
X
n
{\displaystyle X_{n}}
φ
n
{\displaystyle \varphi _{n}}
X
{\displaystyle X}
X
n
→
D
X
{\displaystyle X_{n}{\xrightarrow {\mathcal {D}}}X}
n
→
∞
{\displaystyle n\to \infty }
如果
φ
n
→
pointwise
φ
{\displaystyle \varphi _{n}\quad {\xrightarrow {\textrm {pointwise}}}\quad \varphi }
n
→
∞
{\displaystyle n\to \infty }
且
φ
(
t
)
{\displaystyle \varphi (t)}
t
=
0
{\displaystyle \ t=0}
φ
{\displaystyle \varphi }
X
{\displaystyle X}
勒維連續定理可以用來證明弱大數法則 。
在累積機率分布函數與特徵函數之間存在對射 。也就是說,兩個不同的機率分布不能有相同的特徵函數。
給定一個特徵函數φ,可以用以下公式求得對應的累積機率分布函數
F
{\displaystyle F}
F
X
(
y
)
−
F
X
(
x
)
=
lim
τ
→
+
∞
1
2
π
∫
−
τ
+
τ
e
−
i
t
x
−
e
−
i
t
y
i
t
φ
X
(
t
)
d
t
{\displaystyle F_{X}(y)-F_{X}(x)=\lim _{\tau \to +\infty }{\frac {1}{2\pi }}\int _{-\tau }^{+\tau }{\frac {e^{-itx}-e^{-ity}}{it}}\,\varphi _{X}(t)\,dt}
一般地,這是一個廣義積分 ;被積分的函數可能只是條件可積而不是勒貝格可積 的,也就是說,它的絕對值 的積分可能是無窮大。[ 1]
任意一個函數
φ
{\displaystyle \varphi }
μ
{\displaystyle \mu }
φ
{\displaystyle \varphi \,}
φ
(
0
)
=
1
{\displaystyle \varphi (0)=1\,}
φ
{\displaystyle \varphi \,}
正定函數 (注意這是一個複雜的條件,與
φ
>
0
{\displaystyle \varphi >0}
特徵函數對於處理獨立 隨機變數的函數特別有用。例如,如果
X
1
{\displaystyle X_{1}}
X
2
{\displaystyle X_{2}}
X
n
{\displaystyle X_{n}}
S
n
=
∑
i
=
1
n
a
i
X
i
,
{\displaystyle S_{n}=\sum _{i=1}^{n}a_{i}X_{i},\,\!}
其中
a
i
{\displaystyle a_{i}}
S
n
{\displaystyle S_{n}}
φ
S
n
(
t
)
=
φ
X
1
(
a
1
t
)
φ
X
2
(
a
2
t
)
⋯
φ
X
n
(
a
n
t
)
.
{\displaystyle \varphi _{S_{n}}(t)=\varphi _{X_{1}}(a_{1}t)\varphi _{X_{2}}(a_{2}t)\cdots \varphi _{X_{n}}(a_{n}t).\,\!}
特別地,
φ
X
+
Y
(
t
)
=
φ
X
(
t
)
φ
Y
(
t
)
{\displaystyle \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)}
φ
X
+
Y
(
t
)
=
E
(
e
i
t
(
X
+
Y
)
)
=
E
(
e
i
t
X
e
i
t
Y
)
=
E
(
e
i
t
X
)
E
(
e
i
t
Y
)
=
φ
X
(
t
)
φ
Y
(
t
)
{\displaystyle \varphi _{X+Y}(t)=E\left(e^{it(X+Y)}\right)=E\left(e^{itX}e^{itY}\right)=E\left(e^{itX}\right)E\left(e^{itY}\right)=\varphi _{X}(t)\varphi _{Y}(t)}
注意我們需要
X
{\displaystyle X}
Y
{\displaystyle Y}
另外一個特殊情況,是
a
i
=
1
n
{\displaystyle a_{i}={\frac {1}{n}}}
S
n
{\displaystyle S_{n}}
X
¯
{\displaystyle {\overline {X}}}
φ
X
¯
(
t
)
=
(
φ
X
(
t
n
)
)
n
{\displaystyle \varphi _{\overline {X}}(t)=\left(\varphi _{X}\left({\frac {t}{n}}\right)\right)^{n}}
分布
特徵函數
φ
(
t
)
{\displaystyle \varphi (t)}
退化分布
δ
a
{\displaystyle \delta _{a}}
e
i
t
a
{\displaystyle e^{ita}}
伯努利分布
B
e
r
n
(
p
)
{\displaystyle \mathrm {Bern} (p)}
1
−
p
+
p
e
i
t
{\displaystyle 1-p+pe^{it}}
二項分布
B
(
n
,
p
)
{\displaystyle B(n,p)}
(
1
−
p
+
p
e
i
t
)
n
{\displaystyle (1-p+pe^{it})^{n}}
負二項分布
N
B
(
r
,
p
)
{\displaystyle NB(r,p)}
(
1
−
p
1
−
p
e
i
t
)
r
{\displaystyle {\biggl (}{\frac {1-p}{1-pe^{i\,t}}}{\biggr )}^{\!r}}
卜瓦松分布
P
o
i
s
(
λ
)
{\displaystyle \mathrm {Pois} (\lambda )}
e
λ
(
e
i
t
−
1
)
{\displaystyle e^{\lambda (e^{it}-1)}}
連續均勻分布
U
(
a
,
b
)
{\displaystyle U(a,b)}
e
i
t
b
−
e
i
t
a
i
t
(
b
−
a
)
{\displaystyle {\frac {e^{itb}-e^{ita}}{it(b-a)}}}
拉普拉斯分布
L
(
μ
,
b
)
{\displaystyle L(\mu ,b)}
e
i
t
μ
1
+
b
2
t
2
{\displaystyle {\frac {e^{it\mu }}{1+b^{2}t^{2}}}}
常態分布
N
(
μ
,
σ
2
)
{\displaystyle N(\mu ,\sigma ^{2})}
e
i
t
μ
−
1
2
σ
2
t
2
{\displaystyle e^{it\mu -{\frac {1}{2}}\sigma ^{2}t^{2}}}
卡方分布
χ
k
2
{\displaystyle \chi _{k}^{2}}
k
(
1
−
2
i
t
)
−
k
2
{\displaystyle (1-2it)^{-{\frac {k}{2}}}}
柯西分布
C
(
μ
,
θ
)
{\displaystyle C(\mu ,\theta )}
e
i
t
μ
−
θ
|
t
|
{\displaystyle e^{it\mu -\theta |t|}}
伽瑪分布
Γ
(
k
,
θ
)
{\displaystyle \Gamma (k,\theta )}
(
1
−
i
t
θ
)
−
k
{\displaystyle (1-it\theta )^{-k}}
指數分布
E
x
p
(
λ
)
{\displaystyle \mathrm {Exp} (\lambda )}
(
1
−
i
t
λ
−
1
)
−
1
{\displaystyle (1-it\lambda ^{-1})^{-1}}
多元常態分布
N
(
μ
,
Σ
)
{\displaystyle N(\mu ,\Sigma )}
e
i
t
T
μ
−
1
2
t
T
Σ
t
{\displaystyle e^{it^{T}\mu -{\frac {1}{2}}t^{T}\Sigma t}}
多元柯西分布
M
u
l
t
i
C
a
u
c
h
y
(
μ
,
Σ
)
{\displaystyle \mathrm {MultiCauchy} (\mu ,\Sigma )}
[ 2]
e
i
t
T
μ
−
t
T
Σ
t
{\displaystyle e^{it^{T}\mu -{\sqrt {t^{T}\Sigma t}}}}
Oberhettinger (1973) 提供的特徵函數表.
由於連續定理 ,特徵函數被用於中央極限定理 的最常見的證明中。
特徵函數還可以用來求出某個隨機變數的動差 。只要第n 個動差存在,特徵函數就可以微分n 次,得到:
E
(
X
n
)
=
i
−
n
φ
X
(
n
)
(
0
)
=
i
−
n
[
d
n
d
t
n
φ
X
(
t
)
]
t
=
0
.
{\displaystyle \operatorname {E} \left(X^{n}\right)=i^{-n}\,\varphi _{X}^{(n)}(0)=i^{-n}\,\left[{\frac {d^{n}}{dt^{n}}}\varphi _{X}(t)\right]_{t=0}.\,\!}
例如,假設
X
{\displaystyle X}
柯西分布 。那麼
φ
X
(
t
)
=
e
−
|
t
|
{\displaystyle \varphi _{X}(t)=e^{-|t|}}
t
=
0
{\displaystyle t=0}
可微 ,說明柯西分布沒有期望值 。另外,注意到
n
{\displaystyle n}
獨立 的觀測的樣本平均值
X
¯
{\displaystyle {\overline {X}}}
φ
X
¯
(
t
)
=
(
e
−
|
t
|
n
)
n
=
e
−
|
t
|
{\displaystyle \varphi _{\overline {X}}(t)=(e^{-{\frac {\left\vert t\right\vert }{n}}})^{n}=e^{-|t|}}
特徵函數的對數是一個累積量母函數 ,它對於求出累積量是十分有用的;注意有時定義累積量母函數為動差母函數 的對數,而把特徵函數的對數稱為第二 累積量母函數。
具有尺度母數
θ
{\displaystyle \theta }
k 的伽瑪分布 的特徵函數為:
(
1
−
θ
i
t
)
−
k
{\displaystyle (1-\theta \,i\,t)^{-k}}
現在假設我們有:
X
∼
Γ
(
k
1
,
θ
)
{\displaystyle \ X\sim \Gamma (k_{1},\theta )}
Y
∼
Γ
(
k
2
,
θ
)
{\displaystyle \ Y\sim \Gamma (k_{2},\theta )}
其中
X
{\displaystyle X}
Y
{\displaystyle Y}
X
+
Y
{\displaystyle X+Y}
X
{\displaystyle X}
Y
{\displaystyle Y}
φ
X
(
t
)
=
(
1
−
θ
i
t
)
−
k
1
,
φ
Y
(
t
)
=
(
1
−
θ
i
t
)
−
k
2
{\displaystyle \varphi _{X}(t)=(1-\theta \,i\,t)^{-k_{1}},\,\qquad \varphi _{Y}(t)=(1-\theta \,i\,t)^{-k_{2}}}
根據獨立性和特徵函數的基本性質,可得:
φ
X
+
Y
(
t
)
=
φ
X
(
t
)
φ
Y
(
t
)
=
(
1
−
θ
i
t
)
−
k
1
(
1
−
θ
i
t
)
−
k
2
=
(
1
−
θ
i
t
)
−
(
k
1
+
k
2
)
{\displaystyle \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)=(1-\theta \,i\,t)^{-k_{1}}(1-\theta \,i\,t)^{-k_{2}}=\left(1-\theta \,i\,t\right)^{-(k_{1}+k_{2})}}
這就是尺度母數為
θ
{\displaystyle \theta }
k
1
+
k
2
{\displaystyle k_{1}+k_{2}}
X
+
Y
∼
Γ
(
k
1
+
k
2
,
θ
)
{\displaystyle X+Y\sim \Gamma (k_{1}+k_{2},\theta )}
這個結果可以推廣到
n
{\displaystyle n}
∀
i
∈
{
1
,
…
,
n
}
:
X
i
∼
Γ
(
k
i
,
θ
)
⇒
∑
i
=
1
n
X
i
∼
Γ
(
∑
i
=
1
n
k
i
,
θ
)
{\displaystyle \forall i\in \{1,\ldots ,n\}:X_{i}\sim \Gamma (k_{i},\theta )\qquad \Rightarrow \qquad \sum _{i=1}^{n}X_{i}\sim \Gamma \left(\sum _{i=1}^{n}k_{i},\theta \right)}
如果
X
{\displaystyle X}
φ
X
(
t
)
=
E
(
e
i
t
⋅
X
)
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{it\cdot X}\right)}
這裡的點表示向量的點積 ,而向量
t
{\displaystyle t}
X
{\displaystyle X}
對偶空間 內。用更加常見的矩陣表示法,就是:
φ
X
(
t
)
=
E
(
e
i
t
T
X
)
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{it^{T}X}\right)}
如果
X
∼
N
(
0
,
Σ
)
{\displaystyle X\sim N(0,\Sigma )\,}
多元高斯 隨機變數,那麼:
φ
X
(
t
)
=
E
(
e
i
t
T
X
)
=
∫
x
∈
R
n
1
(
2
π
)
n
/
2
|
Σ
|
1
/
2
e
−
1
2
x
T
Σ
−
1
x
⋅
e
i
t
T
x
d
x
=
e
−
1
2
t
T
Σ
t
,
t
∈
R
n
,
{\displaystyle \varphi _{X}(t)=\operatorname {E} \left(e^{it^{T}X}\right)=\int _{x\in \mathbf {R} ^{n}}{\frac {1}{\left(2\pi \right)^{n/2}\left|\Sigma \right|^{1/2}}}\,e^{-{\frac {1}{2}}x^{T}\Sigma ^{-1}x}\cdot e^{it^{T}x}\,dx=e^{-{\frac {1}{2}}t^{T}\Sigma t},\quad t\in \mathbf {R} ^{n},}
其中
|
Σ
|
{\displaystyle |\Sigma |}
正定矩陣 Σ的行列式。
如果
X
{\displaystyle X}
φ
X
(
T
)
=
E
(
e
i
T
r
(
X
T
)
)
{\displaystyle \varphi _{X}(T)=\operatorname {E} \left(e^{i\,\mathrm {Tr} (XT)}\right)}
在這裡,
T
r
(
⋅
)
{\displaystyle \mathrm {Tr} (\cdot )}
跡 函數,
X
T
{\displaystyle \ XT}
T
{\displaystyle T}
X
{\displaystyle X}
XT 一定有跡,因此矩陣X 必須與矩陣T 的轉置 的大小相同;因此,如果X 是m × n 矩陣,那麼T 必須是n × m 矩陣。
注意乘法的順序不重要(
X
T
≠
T
X
{\displaystyle XT\neq TX}
t
r
(
X
T
)
=
t
r
(
T
X
)
{\displaystyle \ tr(XT)=tr(TX)}
矩陣值隨機變數的例子包括威沙特分布 和矩陣常態分布 。
相關概念有動差母函數 和機率母函數 。特徵函數對於所有機率分布都存在,但動差母函數不是這樣。
特徵函數與傅立葉轉換 有密切的關係:一個機率密度函數
p
(
x
)
{\displaystyle p(x)}
p
(
x
)
{\displaystyle p(x)}
連續傅立葉轉換 的共軛複數 (按照通常的慣例)。
φ
X
(
t
)
=
⟨
e
i
t
X
⟩
=
∫
−
∞
∞
e
i
t
x
p
(
x
)
d
x
=
(
∫
−
∞
∞
e
−
i
t
x
p
(
x
)
d
x
)
¯
=
P
(
t
)
¯
,
{\displaystyle \varphi _{X}(t)=\langle e^{itX}\rangle =\int _{-\infty }^{\infty }e^{itx}p(x)\,dx={\overline {\left(\int _{-\infty }^{\infty }e^{-itx}p(x)\,dx\right)}}={\overline {P(t)}},}
其中
P
(
t
)
{\displaystyle P(t)}
p
(
x
)
{\displaystyle p(x)}
連續傅立葉轉換 。類似地,從
φ
X
(
t
)
{\displaystyle \varphi _{X}(t)}
p
(
x
)
{\displaystyle p(x)}
p
(
x
)
=
1
2
π
∫
−
∞
∞
e
i
t
x
P
(
t
)
d
t
=
1
2
π
∫
−
∞
∞
e
i
t
x
φ
X
(
t
)
¯
d
t
{\displaystyle p(x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{itx}P(t)\,dt={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{itx}{\overline {\varphi _{X}(t)}}\,dt}
確實,即使當隨機變數沒有密度時,特徵函數仍然可以視為對應於該隨機變數的測度的傅立葉轉換。
^ P. Levy, Calcul des probabilités, Gauthier-Villars, Paris, 1925. p. 166
^ Kotz et al. p. 37 using 1 as the number of degree of freedom to recover the Cauchy distribution
Lukacs E. (1970) Characteristic Functions. Griffin, London. pp. 350
Bisgaard, T. M., Sasvári, Z. (2000) Characteristic Functions and Moment Sequences, Nova Science










































































![{\displaystyle \operatorname {E} \left(X^{n}\right)=i^{-n}\,\varphi _{X}^{(n)}(0)=i^{-n}\,\left[{\frac {d^{n}}{dt^{n}}}\varphi _{X}(t)\right]_{t=0}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e6b4080fec36ab7150198da6f2dc65061c27e7d)






























