热力学第二定律
| 热力学 |
|---|
 |
热力学第二定律(英語:second law of thermodynamics)是热力学的四条基本定律之一,表述热力学过程的不可逆性——孤立系统自發地朝著熱力學平衡方向──最大熵狀態──演化,同样地,第二类永动机永不可能实现。
這一定律的歷史可追溯至尼古拉·卡诺对于热机效率的研究,及其于1824年提出的卡诺定理[1]:176-177。定律有许多种表述,其中最具代表性的是克勞修斯表述(1850年)和开尔文表述(1851年),这些表述都可被证明是等价的。定律的数学表述主要借助克勞修斯所引入的熵的概念,具体表述为克勞修斯定理。
虽然这一定律在热力学范畴内是一条经验定律,最初无法得到解释,但随着统计力学的发展,这一定律逐渐得到解释[2]:288-292。
这一定律本身及所引入的熵的概念对于物理学及其他科学领域有深远意义。定律本身可作为过程不可逆性[2]:262及时间流向的判据。而路德维希·玻尔兹曼对于熵的微观解释——系统微观粒子无序程度的量度,更使这概念被引用到物理学之外诸多领域,如信息论及生态学等[2]:287。
定律的自然语言表述
[编辑]克勞修斯表述
[编辑]
克勞修斯表述是以热量传递的不可逆性(即热量总是自发地从高温热源流向低温热源)作为出发点。
虽然可以借助冰箱使热量从低温热源流向高温热源,但这过程是借助外界对制冷机做功实现的,即这过程除了有热量的传递,还有功转化为热的其他影响。
1850年克勞修斯将这一规律总结为:
| “ | 不可能把热量从低温物体传递到高温物体而不产生其他影响。[3] | ” |
开尔文表述
[编辑]
开尔文表述是以第二类永动机不可能实现这一规律作为出发点。
第二类永动机是指可以将从单一热源吸热全部转化为功,但大量事实证明这个过程是不可能实现的。功能够自发地、无条件地全部转化为热;但热转化为功是有条件的,而且转化效率有所限制。也就是说功自发转化为热这一过程只能单向进行而不可逆。
1851年开尔文勋爵把这一普遍规律总结为:
| “ | 不可能从单一热源吸收能量,使之完全变为有用功而不产生其他影响。 | ” |
两种表述的等价性
[编辑]上述两种表述可以论证是等价的:
- 如果开尔文表述不真,那么克勞修斯表述不真:假设存在违反开尔文表述的热机A,可以从低温热源吸收热量並将其全部转化为有用功。假設存在热机B,可以把功完全转化为热量并传递给高温热源(这在现实中可实现)。此时若让A、B联合工作,則可以看到从低温热源流向高温热源,而并未产生任何其他影响,即克劳修斯表述不真。
- 如果克勞修斯表述不真,那么开尔文表述不真:假设存在违反克劳修斯表述的制冷机A,可以在不利用外界对其做的功的情况下,使热量由低温热源流向高温热源。假設存在热机B,可以从高温热源吸收热量並将其中的熱量转化为有用功,同时将热量传递给低温热源(这在现实中可实现)。此时若让A、B联合工作,則可以看到A与B联合组成的热机从高温热源吸收热量並将其完全转化为有用功,而并未产生任何其他影响,即开尔文表述不真。
从上述二點,可以看出上述两种表述是等价的。[2]:259-260
卡拉西奥多里原理
[编辑]
卡拉西奥多里原理是康斯坦丁·卡拉西奥多里在1909年给出的公理性表述:
| “ | 在一个系统的任意给定平衡态附近,总有这样的态存在:从给定的态出发,不可能经过绝热过程得到。 | ” |
值得注意的是,卡拉西奥多里原理如果要和开尔文表述及克劳修斯表述等价,需要辅以普朗克原理(起始处于内部热平衡的封闭系统,等体积功总会增加其内能)。[4][5][6][7]
定律的其他表述
[编辑]除上述几种表述外,热力学第二定律还有其他表述。 如针对焦耳热功当量实验的普朗克表述[2]:259-260:
| “ | 不可存在一个机器,在循环动作中把一重物升高而同时使一热库冷却。 | ” |
以及较为近期的黑首保勞-肯南表述(Hatsopoulos-Keenan statement)[8]:
| “ | 对于一个有给定能量,物质组成,参数的系统,存在这样一个稳定的平衡态:其他状态总可以通过可逆过程达到之。 | ” |
可以论证,这些表述与克劳修斯表述以及开尔文表述是等价的[9]。
定律的推论
[编辑]卡诺定理
[编辑]
卡诺定理是尼古拉·卡诺于1824年在《谈谈火的动力和能发动这种动力的机器》中发表的有关热机效率的定理。值得注意的是定理是在热力学第二定律提出20余年前已然提出,从历史角度来说其为热力学第二定律的理论来源。但是卡诺本人给出的证明是在热质说的错误前提下进行的证明[1]:176[2]:265,而对于其相对严密(以热动说为前提,而非热质说)的证明需要热力学第二定律。
定理的表述
[编辑]卡诺定理表述为:
| “ | 1. 在相同的高温热源和低温热源间工作的一切可逆热机的效率都相等。
2. 在相同的高温热源和低温热源间工作的一切热机中,不可逆热机的效率不可能大于可逆热机的效率。 |
” |
卡诺循环
[编辑]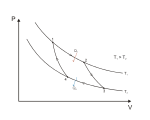
在定理表述中的可逆热机工作機制是按照卡诺于1824年所提出的卡诺循环,是由两个绝热过程,两个等温过程组成的循环。利用热力学第一定律和理想气体状态方程,可以得到其效率。(其中、为热力学温标下高、低温热源温度)
卡诺定理的证明
[编辑]
定理可以利用热力学第二定律的克劳修斯表述进行证明。[2]:266-267
假设存在一违反卡诺定理的不可逆机(图中左边的热机),其效率大于在相同热源和()间工作的可逆机效率。此时可见,当其从吸收热量时,其输出有用功,同时向释放热量。
当可逆机(图中右边的卡诺热机)输出同样多有用功时,其从吸收热量,向释放热量。
此时使可逆机逆向运转(即作为制冷机)并与不可逆机联合工作,不难看出有热量从流向而未产生其他影响,违反克劳修斯表述。则这种不可逆机不可能存在,定理得证。
热力学温标
[编辑]热力学温标是由开尔文勋爵于1848年利用卡诺定理引入的。它是一个相当理想的温标,因为它与测温物质属性无关。
其可以通过下列过程引入[1]:173-176:
由卡诺定理,可逆机效率只与热源的温度有关,而与工作物质无关。考察热机效率的定义(其中为热机对外做功,为热机从高温热源吸热,为热机向低温热源放热)。则可定义一个关于某温标下两热源温度、函数。
经过简单推导,可以证明,对于任意三个温度、、,存在。易见(其中为形式可选择的普适函数),不妨令,则可得出。
这样取定的温标,由于卡诺定理,是与测温物质无关的,即热力学温标(开氏温标)。
由于定义式只给出了两个温度的比值,仍需要一个标准点:取水的三相点,为273.16K。(1954年国际计量大会决定)
克劳修斯定理
[编辑]
克劳修斯定理,又称“克劳修斯不等式”,是克劳修斯于1862年提出以说明系统流入的热量与其熵以及周围环境的关系。这一定理提供了热力学第二定律的数学表述。 定理可由下列过程得到:
- 考察可逆循环的效率,不难得出其总吸热、总放热与热源温度、()存在。由于、以及、分别对应循环的两个等温过程,而在绝热过程中,。可以得到在这个循化过程中[2]:271-272。
- 对于不可逆循环,对循环过程进行微分,与在相同热源的可逆循环进行比较,利用卡诺定理,得到。[10]
综上,可以得到对于一切在给定热源下的工作循环,系统流入的热量与环境温度T存在:。当且仅当工作循环为可逆循环时[11]。
熵
[编辑]熵的热力学定义
[编辑]熵作为状态参量最早由克劳修斯于1854年首次引入,1865年他把这一状态参量命名为Entropie(德语)(来源于希腊语τρoπή, umkehren,转变)。[1]:184[2]:274
其引入过程如下:
考察可逆循环过程中的克劳修斯不等式,可以得到循环中某一过程L(始、末状态分别为a、b)中,只与a,b有关,而与具体路径无关。
则必然存在一态函数:其微分量为,定义这个函数为熵()。
则对于可逆过程L, ,而不可逆过程的熵变可以通过相应的可逆过程求得 。
熵增加原理
[编辑]考察一系列不可逆过程中熵的变化(如在绝热环境中理想气体的真空自由膨胀,在绝热环境中两物体间热传递等等)经过计算,可以得到,这些过程中系统的熵。
而现在已有大量的实验证明:
| “ | 热力学系统从一个平衡态到另一平衡态的过程中,其熵永不减少:若过程可逆,则熵不变;若不可逆,则熵增加。 | ” |
即熵增加原理。
通过熵增加原理,可以得到对于一个孤立系统,其内部自发进行的与热相关的过程必然向熵增的方向进行。而孤立系统不受外界任何影响,且系统最终处于平衡态,则在平衡态时,系统的熵取最大值。由此,熵增加原理则可作为不可逆过程判据。可以证明熵增加原理与克劳修斯表述及开尔文表述等价。[2]:280-284
玻尔兹曼关系
[编辑]
玻尔兹曼关系是对熵的微观(统计意义的)解释,表述为:系统的熵与其微观状态数存在函数关系,其中为玻尔兹曼常数。其可通过热力学第一定律,熵的热力学定义,及麦克斯韦-玻尔兹曼统计推出。值得注意的是这一关系在玻尔兹曼生前并未具体给出,仅在1872年时说明与有正比关系。这一公式首次具体给出是在馬克斯·普朗克的《热辐射》讲义中。[2]:286
玻尔兹曼关系给出了熵的微观解释——系统微观粒子的无序程度的度量,并对熵这一概念引入信息论、生态学等其他领域具有深远意义。
定律的解释
[编辑]由于热力学自身局限性(它仅适用于粒子很多的宏观系统,它把物质视作“连续体”,不考虑物质的微观结构。)[2]:3,因而在热力学自身范畴内,定律只能作为经验定律而不能得到解释。如果要对定律进行解释,需要借助统计力学的方法。引用熵的统计力学解释(玻尔兹曼关系)结合热力学定律,可以对较为典型的不可逆热力学过程进行分析,从而得出对热力学第二定律的解释[2]:288-292:
| “ | 孤立系统的自发过程总是从热力学概率小的宏观状态向热力学概率大的宏观状态转变 | ” |
与热力学其他定律的联系
[编辑]与热力学第一定律的联系
[编辑]热力学第一定律主要从数量上说明功和热量对系统内能改变在数量上的等价性。热力学第二定律揭示了热量与功的转化,及热量传递的不可逆性。两者对于全面的描述一个热力学过程都是不可或缺的。[2]:263-264
与热力学第零定律的联系
[编辑]热力学第零定律是在两物体处于热平衡前提下判定温度,在未达热平衡时不适用。在未达热平衡时可利用热力学第二定律,通过判定热传递方向来判定两物体的温度。[2]:263-264
对定律的诘难
[编辑]麦克斯韦妖
[编辑]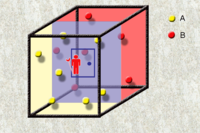

麦克斯韦妖是詹姆斯·麦克斯韦假想存在的一理想模型。麦克斯韦设想了一个容器被分为装有相同温度的同种气体的两部分A、B。麦克斯韦妖看守两部分间“暗门”,可以观察分子运动速度,并使分子运动较快的分子向确定的一部分流动,而较慢的分子向另一部分流动。经过充分长的时间,两部分分子运动的平均速度即温度(参考统计力学中对于温度的微观解释)产生差值并越来越大。经过运算可以得到这一过程是熵减过程,而麦克斯韦妖的存在使这一过程成为自发过程,这是明显有悖于热力学第二定律的。
对其最为有名的回应之一是由利奧·西拉德于1929年提出。西拉德指出如果麦克斯韦妖真正存在,那么它观察分子速度及获取信息的过程必然产生额外的能量消耗, 产生熵。[1]:198
洛施密特悖论
[编辑]
洛施密特悖论,又称可反演性悖论,指出如果对符合具有时间反演性的动力学规律的微观粒子进行反演,那么系统将产生熵减的结果,这是明显有悖于熵增加原理的。
针对这一悖论,玻尔兹曼提出:熵增过程确实并非一个单调过程,但对于一个宏观系统,熵增出现要比熵减出现的概率要大得多;即使达到热平衡,熵也会围绕着其最大值出现一定的涨落,且幅度越大的涨落出现概率越小。[1]:196[12]现在已有的一些实验结果与玻尔兹曼的叙述基本相符。
吉布斯悖论
[编辑]
玻尔兹曼关系给出了一个并不外延的熵的表示方法。这导致产生了一个明显有悖于热力学第二定律的结论,吉布斯悖论——其允许一个封闭系统的熵减少。在通常的解释中,都会引用量子力学中粒子的不可区分性去说明系统中粒子本身性质并不影响系统的熵来避免产生这一悖论。然而现在有越来越多论文采用如是观点:熵阐释的改变恰恰可以忽略由于分子本身排列方式改变所带来的影响。而现有的Sackur-Tetrode方程对于理想气体的熵的解释是外延的。[12]
庞加莱始态复现
[编辑]1892年,昂利·庞加莱证明了这样一个定理:
| “ | 孤立的,有限的保守动力学系统的组态在足夠長久时间後可回复到任意接近初始组态。 | ” |
即庞加莱复现定理。
1896年,恩斯特·策梅洛引用这一定理对于热力学第二定律进行诘难,认为热力学与动力学不兼容,并似乎得到了普朗克以及庞加莱本人的支持。[1]:197针对这一观点,玻尔兹曼引用涨落的概念调和热力学与动力学,认为复现是依靠涨落实现的。据他估计对一个有个(标准情况下,约0.037ml的气体所包含的气体粒子数)粒子的系统,复现时间的数量级为(易见这个数字过分庞大,以致对于时间单位选取是无意义的)[1]:197。而宇宙的年龄约为秒,因而可见,庞加莱始态复现定理对于一个宏观热力学系统是没有现实意义的。
热寂说
[编辑]如果将热力学第一、第二定律运用于宇宙,这一典型的孤立系统,将得到这样的结论:1.宇宙能量守恒,2.宇宙的熵不会减少。那么将得到,宇宙的熵终将达到极大值,即宇宙将最终达到热平衡,称热寂。
在十九世纪,对于热寂说有两个较为有影响的驳斥,一个是由玻尔兹曼提出的“涨落说”(1872)[12],另一个是恩格斯利用运动不灭在《自然辩证法》中进行的驳斥(1876)。现今对于宇宙的理解(1. 宇宙在膨胀;2. 宇宙,作为自引力系统,是具有负热容的不稳定系统)指出宇宙是不稳定的热力学系统,并不像静态宇宙模型所设想的那样具有平衡态,因而其熵亦无最大值,即热寂并不存在。[13]
参阅
[编辑]参考文献
[编辑]- ^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 赵凯华; 罗蔚因. 《新概念物理教程 热学》第二版. 高等教育出版社. ISBN 9787040066777.
- ^ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 秦允豪. 《普通物理学教程 热学》第三版. 高等教育出版社. 2011. ISBN 978-7-04-030090-1.
- ^ Clausius, R. The Mechanical Theory of Heat – with its Applications to the Steam Engine and to Physical Properties of Bodies. London: John van Voorst. 1867 [19 June 2012].
- ^ Planck, M. (1926). Über die Begründing des zweiten Hauptsatzes der Thermodynamik, S.B. Preuß. Akad. Wiss. phys. math. Kl.: 453–463.
- ^ Buchdahl, H.A. (1966). The Concepts of Classical Mechanics, Cambridge University Press, Cambridge UK, p. 69.
- ^ Münster, A. (1970). Classical Thermodynamics, Wiley—Interscience, London, ISBN 978-0-471-62430-1, p. 45.
- ^ Lieb, E.H., Yngvason, J. (1999). The physics and mathematics of the second law of thermodynamics, Phys. Rep., 310: 1–96, p. 49.
- ^ Principles of General Thermodynamics. Krieger, 1981.
- ^ Gyftopoulos, E. P., Beretta, G. P. Thermodynamics: Foundations and Applications. Dover Publications, 2005.
- ^ 范康年. 《物理化学》第二版. 高等教育出版社. 2005: 460. ISBN 7-04-016767-0.
- ^ Clausius theorem (页面存档备份,存于互联网档案馆) at Wolfram Research
- ^ 12.0 12.1 12.2 Von dem c. M. Ludwig Boltzmann in Graz Sitzb. d. Kaiserlichen Akademie der Wissenschaften,mathematich-naturwissen Cl. LXXVI, Abt II, 1877, pp. 373-435.
- ^ 赵凯华. 《定性与半定量物理学》第二版. 高等教育出版社. 2008: 236 - 237. ISBN 978-7-04-022522-8.
扩展阅读
[编辑]- Goldstein, Martin, and Inge F., 1993. The Refrigerator and the Universe. Harvard Univ. Press. Chpts. 4–9 contain an introduction to the Second Law, one a bit less technical than this entry. ISBN 978-0-674-75324-2
- Leff Harvey S., and Rex, Andrew F. (eds.) 2003. Maxwell's Demon 2 : Entropy, classical and quantum information, computing. Bristol UK; Philadelphia PA: Institute of Physics. ISBN 978-0-585-49237-7
- Halliwell, J.J. Physical Origins of Time Asymmetry. Cambridge. 1994. ISBN 978-0-521-56837-1.(technical).
- Carnot, Sadi. Thurston, Robert Henry , 编. Reflections on the Motive Power of Heat and on Machines Fitted to Develop That Power. New York: J. Wiley & Sons. 1890. (full text of 1897 ed. (页面存档备份,存于互联网档案馆)) (html (页面存档备份,存于互联网档案馆))
- Stephen Jay Kline (1999). The Low-Down on Entropy and Interpretive Thermodynamics, La Canada, CA: DCW Industries. ISBN 1-928729-01-0.
- Kostic, M. Revisiting The Second Law of Energy Degradation and Entropy Generation: From Sadi Carnot's Ingenious Reasoning to Holistic Generalization. AIP Conference Proceedings 1411. 2011: 327–350. Bibcode:2011AIPC.1411..327K. CiteSeerX 10.1.1.405.1945
 . ISBN 978-0-7354-0985-9. doi:10.1063/1.3665247.
. ISBN 978-0-7354-0985-9. doi:10.1063/1.3665247. |journal=被忽略 (帮助);|issue=被忽略 (帮助) also at [1].
外部链接
[编辑]- Stanford Encyclopedia of Philosophy: "Philosophy of Statistical Mechanics (页面存档备份,存于互联网档案馆)" – by Lawrence Sklar.
- Second law of thermodynamics (页面存档备份,存于互联网档案馆) in the MIT Course Unified Thermodynamics and Propulsion (页面存档备份,存于互联网档案馆) from Prof. Z. S. Spakovszky
- E.T. Jaynes, 1988, "The evolution of Carnot's principle (页面存档备份,存于互联网档案馆)," in G. J. Erickson and C. R. Smith (eds.)Maximum-Entropy and Bayesian Methods in Science and Engineering, Vol 1: p. 267.
- Caratheodory, C., "Examination of the foundations of thermodynamics," trans. by D. H. Delphenich (页面存档备份,存于互联网档案馆)
- The Second Law of Thermodynamics (页面存档备份,存于互联网档案馆), BBC Radio 4 discussion with John Gribbin, Peter Atkins & Monica Grady (In Our Time, Dec. 16, 2004)
- The Journal of the International Society for the History of Philosophy of Science, 2012 (页面存档备份,存于互联网档案馆)
- 科学智慧火花:热力学第二定律与第二类永动机之错误[失效連結]

























































