调和级数(英語:Harmonic series)是正整數的倒數之和,是发散的无穷级数,表达式为:

| 无穷级数
|
 |
| 无穷级数
|
|
|
|
|
这级数名字源于泛音及泛音列[註 1]:振动的弦的泛音的波长依次是基本波长的 、
、 、
、 ……等。调和序列中,第一项之后的每一项都是相邻两项的调和平均数;而“调和平均数”一词同样也源自音乐。
……等。调和序列中,第一项之后的每一项都是相邻两项的调和平均数;而“调和平均数”一词同样也源自音乐。
早在14世纪,尼克尔·奥里斯姆已经证明调和級數发散,但知道的人不多。17世纪时,皮耶特罗·曼戈里、约翰·伯努利和雅各布·伯努利完成了全部證明工作。
调和序列历来很受建筑师重视;在巴洛克时期尤其明显。当时建筑师在建造教堂和宫殿时,运用调和序列为楼面布置和建筑物高度建立比例,并使室内外的建筑细节间呈现和谐的联系。[1]
 只要有足够多的骨牌,最顶层骨牌离最底层的距离就可以无穷远。可以发现,图中骨牌排列的形状就像顺时针旋转90°的对数函数,也即函数y=1/x的不定积分。
只要有足够多的骨牌,最顶层骨牌离最底层的距离就可以无穷远。可以发现,图中骨牌排列的形状就像顺时针旋转90°的对数函数,也即函数y=1/x的不定积分。
对刚接触这级数的人而言,调和级数违反直觉——尽管随 不断增大,
不断增大, 无限接近0,但它却是发散级数。调和级数也因此成为一些佯谬的原型。“橡皮筋上的蠕虫”就是其中一例。[2]假设蠕虫沿着1米长的橡皮筋爬行,而橡皮筋每分钟匀速伸展1米。如果相对于其所在的橡皮筋,蠕虫的爬行速度是每分钟1厘米,那么它最终会到达橡皮筋的另一头吗?与直觉相反,答案是肯定的:
无限接近0,但它却是发散级数。调和级数也因此成为一些佯谬的原型。“橡皮筋上的蠕虫”就是其中一例。[2]假设蠕虫沿着1米长的橡皮筋爬行,而橡皮筋每分钟匀速伸展1米。如果相对于其所在的橡皮筋,蠕虫的爬行速度是每分钟1厘米,那么它最终会到达橡皮筋的另一头吗?与直觉相反,答案是肯定的: 分钟之后,蠕虫爬行过的距离与橡皮筋总长度的比值为:
分钟之后,蠕虫爬行过的距离与橡皮筋总长度的比值为:
 。
。
调和级数发散(证明见本条目“发散”一节),即 趋于无穷大时级数也趋于无穷大,这比值也必定在某时刻超过1;也就是说,蠕虫最终一定会到达橡皮筋另一头。然而,在这时刻的n的值极其之大,约为
趋于无穷大时级数也趋于无穷大,这比值也必定在某时刻超过1;也就是说,蠕虫最终一定会到达橡皮筋另一头。然而,在这时刻的n的值极其之大,约为 ,超过1040(1后面有40个零)。这也说明了,尽管调和级数确确实实是发散,但它发散的速度非常慢。
,超过1040(1后面有40个零)。这也说明了,尽管调和级数确确实实是发散,但它发散的速度非常慢。
另一例:假设有一堆完全相同的骨牌,可以肯定的是,它们可以叠在一起,并使得每塊骨牌都突出其下方骨牌外一定长度,最终使得最上层的骨牌完全在最底层骨牌以外甚至更远。违反直觉的是,只要骨牌够多,就可以使最上层的骨牌與最底层骨牌水平距離无穷远。[2][3]较简单的证明如下:
设每一块骨牌的长度为 。再设一叠
。再设一叠 塊平衡的骨牌的质心与最底层骨牌最右端的距离为
塊平衡的骨牌的质心与最底层骨牌最右端的距离为 ;在只有1塊骨牌时,质心就在骨牌的几何中心(假设骨牌密度均匀),即
;在只有1塊骨牌时,质心就在骨牌的几何中心(假设骨牌密度均匀),即 。对于一叠刚好平衡的骨牌(即对于任意一层骨牌,在其之上的骨牌的质心恰好落在其边缘),新骨牌不置于其上方(否则使得质心往右偏移而倒塌),而是垫在整叠骨牌之下,并使得原有骨牌的质心刚好落在新骨牌的最左端(则原来的骨牌不会倒塌);设从上往下第n层骨牌突出其下方骨牌的长度为
。对于一叠刚好平衡的骨牌(即对于任意一层骨牌,在其之上的骨牌的质心恰好落在其边缘),新骨牌不置于其上方(否则使得质心往右偏移而倒塌),而是垫在整叠骨牌之下,并使得原有骨牌的质心刚好落在新骨牌的最左端(则原来的骨牌不会倒塌);设从上往下第n层骨牌突出其下方骨牌的长度为 ,则有:
,则有: 。根据质心的坐标系计算公式,可得到新的骨牌叠的质心为:
。根据质心的坐标系计算公式,可得到新的骨牌叠的质心为:

则 ,即
,即 。
。
也就是说,理想的摆法是:最顶层骨牌与第二层之间水平距离是骨牌长度的 ,第二、三层间水平距离是骨牌长度的
,第二、三层间水平距离是骨牌长度的 ,第三、四层之间水平距离是骨牌长度的
,第三、四层之间水平距离是骨牌长度的 ……依此类推。最终,最顶层和最底层骨牌的水平距离是:
……依此类推。最终,最顶层和最底层骨牌的水平距离是:

调和级数发散,当骨牌数目 趋于无穷大时,水平距离也趋于无穷大。
趋于无穷大时,水平距离也趋于无穷大。
比较审敛法[编辑]
![{\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k}}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7e5c68c008dbd2dae3c0383d4f186d61096a69e)

![{\displaystyle =1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dcaa527dd47805da849dcaa20c3af970147e6a8)

因此该级数发散。
积分判别法(integral test)[编辑]
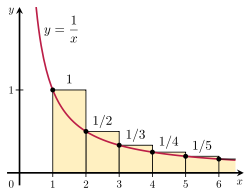
将调和级数的和与一个瑕积分比较可证此级数发散。考虑右图中长方形的排列:长方形宽1单位、高 单位(换句话说,每个长方形的面积都是
单位(换句话说,每个长方形的面积都是 ),所有长方形的总面积就是调和级数的和:
),所有长方形的总面积就是调和级数的和:
矩形面积和

而曲线 以下、从1到正无穷部分的面积由以下瑕积分给出:
以下、从1到正无穷部分的面积由以下瑕积分给出:
曲线下面积
 。这部分面积真包含于(换言之,小于)长方形总面积,长方形的总面积也必定趋于无穷。更准确说,这证明了
。这部分面积真包含于(换言之,小于)长方形总面积,长方形的总面积也必定趋于无穷。更准确说,这证明了

这方法的拓展即积分判别法。
反证法[编辑]
假设调和级数收敛 , 则
但与 矛盾,故假设不真,即调和级数发散。
矛盾,故假设不真,即调和级数发散。
发散率[编辑]
调和级数发散的速度非常缓慢。举例来说,调和序列前1043项的和还不足100。[4]调和数列的部分和呈对数增长。特别地,

其中 是欧拉-马歇罗尼常数,而
是欧拉-马歇罗尼常数,而 约等于
约等于 ,并且随着
,并且随着 趋于正无穷而趋于
趋于正无穷而趋于 。这结果由欧拉给出。
。这结果由欧拉给出。
当然无论调和级数发散率再怎样低,其都不是发散率最慢的级数,仍存在发散率比调和级数更低的级数。理论上没有发散率“最慢”的发散性级数和。
部分和[编辑]
调和级数的第 項部分和为:
項部分和为:
 ,
,
也叫作第n个调和数。
第n个调和数与 的自然对数的差值(即
的自然对数的差值(即 )收敛于欧拉-马歇罗尼常数。
)收敛于欧拉-马歇罗尼常数。
两个不同的调和数之间的差值永远不是整数。
除了 以外,没有任何调和数是整数。[5]
以外,没有任何调和数是整数。[5]
相关级数[编辑]
交错调和级数[编辑]
 此图显示,交错调和级数的前14項部分和(图中黑色线段)收敛于2的自然对数(红色直线)。
此图显示,交错调和级数的前14項部分和(图中黑色线段)收敛于2的自然对数(红色直线)。
如下级数:

称作交错调和级数。这级数可经交错级数判别法证明收敛。特别地,这级数的和等于2的自然对数:
 。
。
这公式是墨卡托级数(自然对数的泰勒级数形式)的特例。
从反正切函数的泰勒展开式可导出相关级数:
 。
。
这级数也称作π的莱布尼茨公式。
广义调和级数[编辑]
广义调和级数是指有如下形式的级数:
 。
。
其中 且
且 为实数。
为实数。
由比较审敛法可证所有广义调和级数均发散。[6]
 -级数[编辑]
-级数[编辑]
调和级数广义化的其中一種结果是 -级数,定义如下:
-级数,定义如下:
 ,
,
P是任何正实数。当 ,
, -级数即调和级数。由积分判别法或柯西稠密判定法可知
-级数即调和级数。由积分判别法或柯西稠密判定法可知 -级数在
-级数在 时收敛(此时级数又叫过调和级数(over-harmonic series)),而在
时收敛(此时级数又叫过调和级数(over-harmonic series)),而在 时发散。当
时发散。当 时,
时, -级数的和即
-级数的和即 ,也就是黎曼ζ函数在
,也就是黎曼ζ函数在 的值。
的值。
 -级数[编辑]
-级数[编辑]
对凸实值函数 ,若满足以下条件:
,若满足以下条件:

则级数 收敛。
收敛。
随机调和级数[编辑]
随机调和级数定义如下:
 ,
,
其中 是恒等分布的独立随机变量,取值范围为+1和-1,取这两值的概率都是
是恒等分布的独立随机变量,取值范围为+1和-1,取这两值的概率都是 。阿尔伯塔大学的拜伦·施姆兰研究此级数的性质,[7][8]并发现这级数收敛的概率为1,并发现这随机变量有些有趣的性质。特别地,这随机变量的概率密度函数在+2和-2处的值为0.124999999999999999999999999999999999999999764…,与
。阿尔伯塔大学的拜伦·施姆兰研究此级数的性质,[7][8]并发现这级数收敛的概率为1,并发现这随机变量有些有趣的性质。特别地,这随机变量的概率密度函数在+2和-2处的值为0.124999999999999999999999999999999999999999764…,与 只差不到10−42。施姆兰的论文解释了为什么这概率如此接近、但却不是
只差不到10−42。施姆兰的论文解释了为什么这概率如此接近、但却不是 。这概率的精确值由无穷余弦乘积积分
。这概率的精确值由无穷余弦乘积积分 除以
除以 而给出的。[9]
而给出的。[9]
贫化调和级数[编辑]
贫化调和级数是将调和级数中、分母含有数字9的项去除后所剩的级数。这级数是收敛的,其和小於80。[10]实际上,将包含任意数字串的项从调和级数中去除后,所剩级数都收敛。
拉马努金求和[编辑]
调和级数是柯西发散的,而且很多常用的发散级数求和方法[註 2]对它也不适用。但是,调和级数的拉马努金求和存在,且为欧拉-马斯刻若尼常数。
- ^ George L. Hersey, Architecture and Geometry in the Age of the Baroque, p 11-12 and p37-51.
- ^ 2.0 2.1 Graham, Ronald; Knuth, Donald E.; Patashnik, Oren, Concrete Mathematics 2nd, Addison-Wesley: 258–264, 1989, ISBN 978-0-201-55802-9
- ^ Sharp, R.T., Problem 52: Overhanging dominoes, Pi Mu Epsilon Journal, 1954: 411–412
- ^ Sequence A082912 in the On-Line Encyclopedia of Integer Sequences
- ^ Weisstein, Eric W. (编). Harmonic Number. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2011-01-16]. (原始内容存档于2013-05-16) (英语).
- ^ Art of Problem Solving:
"General Harmonic Series" (页面存档备份,存于互联网档案馆)
- ^ "Random Harmonic Series", American Mathematical Monthly 110, 407-416, May 2003
- ^ Schmuland's preprint of Random Harmonic Series (PDF). [2011-01-16]. (原始内容 (PDF)存档于2011-06-08).
- ^ Weisstein, Eric W. (编). Infinite Cosine Product Integral. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2010-11-14]. (原始内容存档于2011-12-28) (英语).
- ^ Nick's Mathematical Puzzles: Solution 72. [2011-01-16]. (原始内容存档于2010-09-28).
外部链接[编辑]

























![{\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k}}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7e5c68c008dbd2dae3c0383d4f186d61096a69e)

![{\displaystyle =1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dcaa527dd47805da849dcaa20c3af970147e6a8)




































