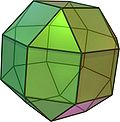
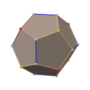
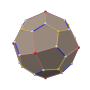
筝形二十四面体

筝形二十四面体

（按这里观看旋转模型）
类别	卡塔兰立体
对偶多面体	小斜方截半立方体
识别
鲍尔斯缩写	sladid
数学表示法
考克斯特符号
康威表示法	oC deC
性质
面	24
边	48
顶点	26
欧拉特征数	F=24, E=48, V=26 （χ=2）
二面角	138°07′05″ arccos(−7 + 4√2/17)
组成与布局
面的种类	筝形
面的布局	V3.4.4.4
顶点图	V3.4.4.4
对称性
对称群	Oh, BC3, [4,3], *432
旋转对称群	O, [4,3]+, (432)
特性
凸、 面可递
图像
V3.4.4.4 （顶点图） 小斜方截半立方体 （对偶多面体） （展开图）

在几何学中，筝形二十四面体（亦称为四角化二十四面体或梯形二十四面体）是一种卡塔兰立体，由24个筝形组成，其对偶多面体为小斜方截半立方体。

性质

筝形二十四面体由24个面、48条边、26个顶点组成，其中24个面为24个全等的筝形、48条边中有24条等长的长边和24条等长的短边、26个顶点中有8个顶点是3个筝形的公共顶点，对应的顶角是三面角；以及6个顶点是4个筝形的公共顶点，对应的顶角是四面角；剩下的12个顶点也是4个筝形的公共顶点，对应的顶角也是四面角，但角度与前者不同。它的对偶多面体是小斜方截半立方体。

面的组成

筝形二十四面体由24个全等的筝形（亦称为鸢形）所组成：

该筝形或筝形的长短边长比为1:(2 − 1/√2) ≈ 1:7000129289300000000♠1.292893...，有3个角等角，其角度分别为(115.26°,81.58°,81.58°,81.58°)

体积与表面积

一个最短边边长为a的筝形二十四面体，其表面积A、体积是V为：

${\begin{aligned}A&=6{\sqrt {29-2{\sqrt {2}}}}\,a^{2}\\V&={\sqrt {122+71{\sqrt {2}}}}\,a^{3}\end{aligned}}$

顶点坐标

若其对偶多面体小斜方截半立方体的边长为单位长，则对应的几何中心位于原点的筝形二十四面体，顶点坐标为：

$\left(0\,,\quad 0\,,\quad \pm {\sqrt {2}}\right)$

$\left(\pm {\sqrt {2}}\,,\quad 0\,,\quad 0\right)$

$\left(0\,,\quad \pm {\sqrt {2}}\,,\quad 0\right)$

$\left(\pm 1\,,\quad 0\,,\quad \pm 1\right)$

$\left(\pm 1\,,\quad \pm 1\,,\quad 0\right)$

$\left(0\,,\quad \pm 1\,,\quad \pm 1\right)$

$\left(\pm {\frac {4+{\sqrt {2}}}{7}}\,,\quad \pm {\frac {4+{\sqrt {2}}}{7}}\,,\quad \pm {\frac {4+{\sqrt {2}}}{7}}\right)$

正交投影

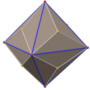
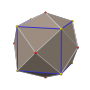
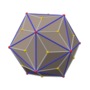
筝形二十四面体有三种从顶点投影的高对称性正交投影。后两者的对偶图其对称性对应于B₂和A₂的考克斯特平面。

正交投影

投影对称性	[2]	[4]	[6]
图像
对偶图像

使用

在文化中，筝形二十四面体出现在部分艺术创作中，例如莫里兹·柯尼利斯·艾雪的艺术创作《星星》以及马兰·布洛克的装置艺术《永恒的水》。此外，亦有部分24个面的多面体骰子被设计为筝形二十四面体的外型，其他常见的24面骰子有三角化八面体、四角化六面体、伪筝形二十四面体、偏方二十四面体和五角二十四面体等形状。

在化学中，部分物质的结晶形状是筝形二十四面体。例如，在自然界中，方沸石和石榴石的晶体结构就是筝形二十四面体，部分实验中制备的氧化铟奈米晶体亦是这种形状。在矿物学中，这种晶体形状称为偏方面体（英语：Trapezohedron），但在几何学中偏方面体则有其他含意，表示反柱体的对偶多面体。 此外在某些情况下会结晶出较不规则的筝形二十四面体，其在结晶学中称为偏方二十四面体（英语：diplohedron）。

• 
  筝形二十四面体外型的骰子。
• 
  马兰·布洛克《永恒的水》
• 
  白榴石的晶体
• 
  钙铁榴石的晶体
• 
  方沸石的晶体
• 
  巴西锰铝石榴石的晶体

相关多面体与镶嵌

投影到球面的筝形二十四面体

若将筝形二十四面体投影到球面上，如右图所示，则其边会与复合八面体立方体（立方体和其对偶——正八面体在空间中互相重叠组合成的结构）投影到球面上的果共用相同的棱。

筝形二十四面体

复合八面体立方体与左图同一个角度

筝形二十四面体是小斜方截半立方体的对偶多面体，而小斜方截半立方体可以经由立方体或正八面体透过扩展变换来构造。其他可以由立方体或正八面体透过康威变换构造的立体及其对偶有：

半正正八面体家族多面体

对称性: [4,3], (*432)							[4,3]+, (432)	[1+,4,3], (*332)	[4,3+], (3*2)
{4,3}	t0,1{4,3}	t1{4,3}	t1,2{4,3}	{3,4}	t0,2{4,3}	t0,1,2{4,3}	s{4,3}	h{4,3}	h1,2{4,3}
半正多面体的对偶
V4.4.4	V3.8.8	V3.4.3.4	V4.6.6	V3.3.3.3	V3.4.4.4	V4.6.8	V3.3.3.3.4	V3.3.3	V3.3.3.3.3

*变异的n42对称性对偶扩展镶嵌系列：V3.4.n.4

对称性 *n32 [n,3]	球面镶嵌				欧氏镶嵌	紧凑双曲		仿紧双曲
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
图像 面布局	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.∞.4
对偶 顶点布局	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

偏方二十四面体

晶体学中的偏方二十四面体。

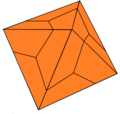
偏方二十四面体为筝形二十四面体的一种变体，其拓朴结构与筝形二十四面体等价。筝形二十四面体与偏方二十四面体的拓朴结构皆与立方体每个面的正方形用两条垂直线分成四个小正方形的结果等价。其可以投影到正八面体上并将每个三角形面分成3个筝形。 在晶体学中，透过旋转其三面角所形成的变体称为dyakis dodecahedron或diploid，然而这些变体在中文文献中皆被称为偏方二十四面体。

八面体群, Oh, 24阶		五角十二面体群, Th, 12阶

筝形二十四面体图

在图论的数学领域中，与筝形二十四面体相关的图为筝形二十四面体图（Disdyakis Dodecahedral Graph），是筝形二十四面体之边与顶点的图，是一个阿基米德对偶图。

性质

筝形二十四面体图有48条边和26个顶点，其中度为3的顶点有8个、度为4的顶点有18个。

其特征多项式为：

$x^{8}{\left(x^{2}-14\right)}{\left(x^{2}-8\right)}^{3}{\left(x^{2}-2\right)}^{5}$

参见

• 筝形六十面体
• 四角化六面体——另外一个卡塔兰二十四面体
• 伪筝形二十四面体

参考文献

1. Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X.  (Section 3-9)
2. Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371  (The thirteen semiregular convex polyhedra and their duals, Page 23, Deltoidal icositetrahedron)

外部链接

• 埃里克·韦斯坦因, 筝形二十四面体 （参阅卡塔兰立体） 于MathWorld（英文）
• Deltoidal (Trapezoidal) Icositetrahedron – Interactive Polyhedron model