补集

在集合论和数学的其他分支中，存在补集的两种定义：相对补集和绝对补集。

相对补集

相对补集$A\setminus B$

若$A$和$B$是集合，则$A$在$B$中的相对补集是由所有属于$B$但不属于$A$的元素组成的集合。

$A$在$B$中的相对补集记为$B\setminus A$或$B-A$。

形式上：

$B\setminus A=\{x\in B\mid x\not \in A\}$

例如：

• $\{1,2,3\}\setminus \{2,3,4\}=\{1\}$
• $\{2,3,4\}\setminus \{1,2,3\}=\{4\}$
• 若$\mathbb {R}$是实数集合，$\mathbb {Q}$是有理数集合，则$\mathbb {R} \setminus \mathbb {Q}$为无理数集合。

下列命题给出一些相对补集同并集和交集等集合论运算相关的一些常用性质。

命题1：若$A,B,C$是集合，则下列等式恒成立：

• $C\setminus (A\cap B)=(C\setminus A)\cup (C\setminus B)$
• $C\setminus (A\cup B)=(C\setminus A)\cap (C\setminus B)$
• $C\setminus (B\setminus A)=(A\cap C)\cup (C\setminus B)$
• $(B\setminus A)\cap C=(B\cap C)\setminus A=B\cap (C\setminus A)$
• $(B\setminus A)\cup C=(B\cup C)\setminus (A\setminus C)$
• $A\setminus A=\varnothing$
• $\varnothing \setminus A=\varnothing$
• $A\setminus \varnothing =A$

绝对补集

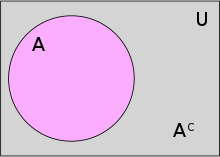
绝对补集$A^{\complement }$

若给定全集$U$，则$A$在$U$中的相对补集称为$A$的绝对补集（简称补集），记为$A^{\complement }$，即：

$A^{\complement }=U\setminus A$

（注意：根据ISO与中华人民共和国国家标准，$A$中子集$B$的补集记作$\complement _{A}B$。）

例如，若全集为自然数集合，则奇数集合的补集为偶数集合。

下列命题给出一些绝对补集同并集和交集等集合论运算相关的一些重要性质。

命题2：若$A$和$B$是全集$U$的子集，则下列恒等式成立：

德摩根定律：

• $(A\cup B)^{\complement }=A^{\complement }\cap B^{\complement }$
• $(A\cap B)^{\complement }=A^{\complement }\cup B^{\complement }$

补集律：

• $A\cup A^{\complement }=U$
• $A\cap A^{\complement }=\varnothing$
• $\varnothing ^{\complement }=U$
• $U^{\complement }=\varnothing$

对合：

• $(A^{\complement })^{\complement }=A$

相对补集和绝对补集的关系：

• $A\setminus B=A\cap B^{\complement }$
• $(A\setminus B)^{\complement }=A^{\complement }\cup B$

上述表明，若$A$为$U$的非空子集，则${A,A^{\complement }}$是$U$的一个分割。

补集的符号

补集的符号在Unicode中为数学运算符区段中的“∁”（Unicode：U+2201）。

参见

• 集合代数
• 朴素集合论
• 对称差
• 布尔逻辑
• 交集
• 并集