歐拉公式 (英語:Euler's formula ,又稱尤拉公式 )是複分析 領域的公式,它將三角函數 與複指數函數 關聯起來,因其提出者萊昂哈德·歐拉 而得名。歐拉公式提出,對任意實數
x
{\displaystyle x}
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
其中
e
{\displaystyle e}
自然對數的底數 ,
i
{\displaystyle i}
虛數單位 ,而
cos
{\displaystyle \cos }
sin
{\displaystyle \sin }
餘弦 、正弦 對應的三角函數 ,參數
x
{\displaystyle x}
弧度 為單位[ 1] cis x c osine plus i s inei 乘以正弦)。由於該公式在
x
{\displaystyle x}
複數 時仍然成立,所以也有人將這一更通用的版本稱為歐拉公式[ 2]
歐拉公式在數學、物理和工程領域應用廣泛。物理學家理查德·費曼 將歐拉公式稱為:「我們的珍寶」和「數學中最非凡的公式」[ 3]
當
x
=
π
{\displaystyle x=\pi }
e
i
π
+
1
=
0
{\displaystyle {{{e}^{{i}\,{\pi }}}+{1}}=0}
歐拉恆等式 。
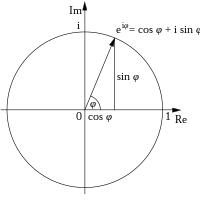
這公式可以說明當
x
{\displaystyle x}
實數 時,函數
e
i
x
{\displaystyle e^{ix}}
複數 平面描述一單位圓 。且
x
{\displaystyle x}
笛卡爾坐標系 描述,歐拉公式在此提供複點至極坐標 的變換
任何複數
z
=
x
+
y
i
{\displaystyle z=x+yi}
z
=
x
+
i
y
=
|
z
|
(
cos
ϕ
+
i
sin
ϕ
)
=
|
z
|
e
i
ϕ
{\displaystyle z=x+iy=|z|(\cos \phi +i\sin \phi )=|z|e^{i\phi }\,}
z
¯
=
x
−
i
y
=
|
z
|
(
cos
ϕ
−
i
sin
ϕ
)
=
|
z
|
e
−
i
ϕ
{\displaystyle {\bar {z}}=x-iy=|z|(\cos \phi -i\sin \phi )=|z|e^{-i\phi }\,}
在此
x
=
R
e
{
z
}
{\displaystyle x=\mathrm {Re} \{z\}\,}
y
=
I
m
{
z
}
{\displaystyle y=\mathrm {Im} \{z\}\,}
|
z
|
=
x
2
+
y
2
{\displaystyle |z|={\sqrt {x^{2}+y^{2}}}}
z
{\displaystyle z}
模
ϕ
=
a
t
a
n
2
(
y
,
x
)
{\displaystyle \phi =\mathrm {atan2} {(y,x)}}
a
t
a
n
2
(
y
,
x
)
=
{
arctan
(
y
x
)
x
>
0
π
+
arctan
(
y
x
)
y
≥
0
,
x
<
0
−
π
+
arctan
(
y
x
)
y
<
0
,
x
<
0
π
2
y
>
0
,
x
=
0
−
π
2
y
<
0
,
x
=
0
undefined
y
=
0
,
x
=
0
{\displaystyle \mathrm {atan2} {(y,x)}={\begin{cases}\arctan \left({\frac {y}{x}}\right)&\qquad x>0\\\pi +\arctan \left({\frac {y}{x}}\right)&\qquad y\geq 0,x<0\\-\pi +\arctan \left({\frac {y}{x}}\right)&\qquad y<0,x<0\\{\frac {\pi }{2}}&\qquad y>0,x=0\\-{\frac {\pi }{2}}&\qquad y<0,x=0\\{\text{undefined}}&\qquad y=0,x=0\end{cases}}}
約翰·伯努利 注意到有[ 4]
1
1
+
x
2
=
1
2
(
1
1
−
i
x
+
1
1
+
i
x
)
.
{\displaystyle {\frac {1}{1+x^{2}}}={\frac {1}{2}}\left({\frac {1}{1-ix}}+{\frac {1}{1+ix}}\right).}
並且由於
∫
d
x
1
+
a
x
=
1
a
ln
(
1
+
a
x
)
+
C
,
{\displaystyle \int {\frac {dx}{1+ax}}={\frac {1}{a}}\ln(1+ax)+C,}
上述公式通過把自然對數和複數(虛數)聯繫起來,告訴我們關於複對數 的一些資訊。然而伯努利並沒有計算出這個積分。
歐拉也知道上述方程,伯努利對歐拉的回應表明他還沒有完全理解複對數。歐拉指出複對數可以有無窮多個值。
與此同時,羅傑·柯特斯 [ 5]
i
x
=
ln
(
cos
x
+
i
sin
x
)
.
{\displaystyle ix=\ln(\cos x+i\sin x).}
由於三角函數的週期性,一個複數可以加上 2i π
1740年左右,歐拉把注意力從對數轉向指數函數,得到了以他命名的歐拉公式。歐拉公式通過比較指數的級數展開和三角函數得到(其實此證法存在問題,原因見驗證方法 ,但結論正確。),於1748年發表[ 6] [ 5]
大約50年之後,卡斯帕爾·韋塞爾 提出可以把複數視做複數平面 中的點。
對於任意實數
x
{\displaystyle x\,}
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
由此也可以推導出
sin
x
=
e
i
x
−
e
−
i
x
2
i
{\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}
cos
x
=
e
i
x
+
e
−
i
x
2
{\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}}
當
x
=
π
{\displaystyle x=\pi \,}
e
i
π
+
1
=
0
{\displaystyle {{{e}^{{i}\,{\pi }}}+{1}}=0}
首先,在複數域上對
e
x
{\displaystyle e^{x}\,}
對於
a
,
b
∈
R
,
c
=
a
+
i
b
∈
C
{\displaystyle a,b\in \mathbb {R} ,c=a+ib\in \mathbb {C} }
e
c
=
lim
n
→
∞
(
1
+
c
n
)
n
{\displaystyle e^{c}=\lim _{n\rightarrow \infty }(1+{\frac {c}{n}})^{n}}
對複數的極坐標表示
w
=
u
+
i
v
=
r
(
cos
θ
+
i
sin
θ
)
{\displaystyle w=u+iv=r(\cos \theta +i\sin \theta )}
r
=
u
2
+
v
2
∈
R
,
θ
=
arctan
(
v
u
)
∈
R
{\displaystyle r={\sqrt {u^{2}+v^{2}}}\in \mathbb {R} ,\theta =\arctan({\frac {v}{u}})\in \mathbb {R} }
且根據狄默夫公式 ,
w
n
=
(
u
+
i
v
)
n
=
r
n
(
cos
n
θ
+
i
sin
n
θ
)
{\displaystyle w^{n}=(u+iv)^{n}=r^{n}(\cos n\theta +i\sin n\theta )}
從而有:
(
1
+
a
+
b
i
n
)
n
=
[
(
1
+
a
n
)
+
i
b
n
]
n
=
r
n
(
cos
θ
n
+
i
sin
θ
n
)
{\displaystyle (1+{\frac {a+bi}{n}})^{n}=[(1+{\frac {a}{n}})+i{\frac {b}{n}}]^{n}=r_{n}(\cos \theta _{n}+i\sin \theta _{n})}
假設
n
>
|
a
|
{\displaystyle n>|a|}
r
n
=
[
(
1
+
a
n
)
2
+
(
b
n
)
2
]
n
2
,
θ
n
=
n
arctan
b
n
1
+
a
n
{\displaystyle r_{n}=[(1+{\frac {a}{n}})^{2}+({\frac {b}{n}})^{2}]^{\frac {n}{2}},\theta _{n}=n\arctan {\frac {\frac {b}{n}}{1+{\frac {a}{n}}}}}
(由於包含n在冪,所以要ln)從而有:
lim
n
→
∞
ln
r
n
=
lim
n
→
∞
[
n
2
ln
(
1
+
2
a
n
+
a
2
+
b
2
n
2
)
]
=
lim
n
→
∞
[
n
2
(
2
a
n
+
a
2
+
b
2
n
2
)
]
=
a
{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }\ln r_{n}&=\lim _{n\rightarrow \infty }[{\frac {n}{2}}\ln(1+{\frac {2a}{n}}+{\frac {a^{2}+b^{2}}{n^{2}}})]\\&=\lim _{n\rightarrow \infty }[{\frac {n}{2}}({\frac {2a}{n}}+{\frac {a^{2}+b^{2}}{n^{2}}})]\\&=a\\\end{aligned}}}
這一步驟用到
ln
(
1
+
x
)
≈
x
{\displaystyle \ln(1+x)\approx x}
墨卡托級數 )
lim
n
→
∞
r
n
=
lim
n
→
∞
e
ln
r
n
=
e
a
{\displaystyle \lim _{n\rightarrow \infty }r_{n}=\lim _{n\rightarrow \infty }e^{\ln r_{n}}=e^{a}}
又有(arctan x 約等於x 於0附近):
lim
n
→
∞
θ
n
=
lim
n
→
∞
(
n
arctan
b
n
1
+
a
n
)
=
lim
n
→
∞
(
n
b
n
1
+
a
n
)
=
b
{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }\theta _{n}&=\lim _{n\rightarrow \infty }(n\arctan {\frac {\frac {b}{n}}{1+{\frac {a}{n}}}})\\&=\lim _{n\rightarrow \infty }(n{\frac {\frac {b}{n}}{1+{\frac {a}{n}}}})\\&=b\\\end{aligned}}}
從而可以證明:
lim
n
→
∞
(
1
+
a
+
b
i
n
)
n
=
e
a
(
cos
b
+
i
sin
b
)
{\displaystyle \lim _{n\rightarrow \infty }(1+{\frac {a+bi}{n}})^{n}=e^{a}(\cos b+i\sin b)}
即:
e
a
+
i
b
=
e
a
(
cos
b
+
i
sin
b
)
{\displaystyle e^{a+ib}=e^{a}(\cos b+i\sin b)}
令
a
=
0
{\displaystyle a=0}
證畢。[ 7]
方法一:泰勒級數
把函數
e
x
{\displaystyle e^{x}\,}
cos
x
{\displaystyle \cos x\,}
sin
x
{\displaystyle \sin x\,}
e
x
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
{\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots }
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
⋯
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots }
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
⋯
{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots }
將
x
=
i
z
{\displaystyle x=iz\,}
e
x
{\displaystyle e^{x}\,}
e
i
z
=
1
+
i
z
+
(
i
z
)
2
2
!
+
(
i
z
)
3
3
!
+
(
i
z
)
4
4
!
+
(
i
z
)
5
5
!
+
(
i
z
)
6
6
!
+
(
i
z
)
7
7
!
+
(
i
z
)
8
8
!
+
⋯
=
1
+
i
z
−
z
2
2
!
−
i
z
3
3
!
+
z
4
4
!
+
i
z
5
5
!
−
z
6
6
!
−
i
z
7
7
!
+
z
8
8
!
+
⋯
=
(
1
−
z
2
2
!
+
z
4
4
!
−
z
6
6
!
+
z
8
8
!
−
⋯
)
+
i
(
z
−
z
3
3
!
+
z
5
5
!
−
z
7
7
!
+
⋯
)
=
cos
z
+
i
sin
z
{\displaystyle {\begin{aligned}e^{iz}&=1+iz+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+{\frac {(iz)^{5}}{5!}}+{\frac {(iz)^{6}}{6!}}+{\frac {(iz)^{7}}{7!}}+{\frac {(iz)^{8}}{8!}}+\cdots \\&=1+iz-{\frac {z^{2}}{2!}}-{\frac {iz^{3}}{3!}}+{\frac {z^{4}}{4!}}+{\frac {iz^{5}}{5!}}-{\frac {z^{6}}{6!}}-{\frac {iz^{7}}{7!}}+{\frac {z^{8}}{8!}}+\cdots \\&=\left(1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+{\frac {z^{8}}{8!}}-\cdots \right)+i\left(z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+\cdots \right)\\&=\cos z+i\sin z\end{aligned}}}
方法二:求導法
對於所有
x
∈
I
{\displaystyle x\in I}
f
(
x
)
=
cos
x
+
i
sin
x
e
i
x
{\displaystyle f(x)={\frac {\cos x+i\sin x}{e^{ix}}}}
由於
e
i
x
⋅
e
−
i
x
=
e
0
=
1
{\displaystyle e^{ix}\cdot e^{-ix}=e^{0}=1}
可知
e
i
x
{\displaystyle e^{ix}\,}
f
(
x
)
{\displaystyle f(x)\,}
f
′
(
x
)
=
(
−
sin
x
+
i
cos
x
)
⋅
e
i
x
−
(
cos
x
+
i
sin
x
)
⋅
i
⋅
e
i
x
(
e
i
x
)
2
=
−
sin
x
⋅
e
i
x
−
i
2
sin
x
⋅
e
i
x
(
e
i
x
)
2
=
−
sin
x
⋅
e
i
x
+
sin
x
⋅
e
i
x
(
e
i
x
)
2
=
0
{\displaystyle {\begin{aligned}f'(x)&={\frac {(-\sin x+i\cos x)\cdot e^{ix}-(\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^{2}}}\\&={\frac {-\sin x\cdot e^{ix}-i^{2}\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&={\frac {-\sin x\cdot e^{ix}+\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&=0\end{aligned}}}
設
[
a
,
b
]
∈
I
{\displaystyle [a,b]\in I}
c
∈
(
a
,
b
)
{\displaystyle c\in (a,b)}
f
′
(
c
)
=
f
(
b
)
−
f
(
a
)
b
−
a
.
{\displaystyle f'(c)={\frac {f(b)-f(a)}{b-a}}.}
拉格朗日中值定理 )
∵
f
′
(
x
)
=
0
{\displaystyle \because f'(x)=0}
∴
f
′
(
c
)
=
0
{\displaystyle \therefore f'(c)=0}
f
(
a
)
=
f
(
b
)
{\displaystyle f(a)=f(b)}
因此
f
(
x
)
{\displaystyle f(x)\,}
常數函數 。
f
(
x
)
=
f
(
0
)
{\displaystyle f(x)=f(0)}
{\displaystyle }
cos
x
+
i
sin
x
e
i
x
=
cos
0
+
i
sin
0
e
0
=
1
{\displaystyle {\frac {\cos x+i\sin x}{e^{ix}}}={\frac {\cos 0+i\sin 0}{e^{0}}}=1}
重新整理,即可得到:
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
方法三:微積分
找出一個原函數
y
(
x
)
{\displaystyle y(x)}
d
y
d
x
=
i
y
{\displaystyle {\frac {dy}{dx}}=iy}
y
(
0
)
=
1
{\displaystyle y(0)=1}
假設
y
(
x
)
=
e
i
x
{\displaystyle y(x)=e^{ix}}
d
d
x
e
i
x
=
i
e
i
x
=
i
y
{\displaystyle {\frac {d}{dx}}e^{ix}=ie^{ix}=iy}
假設
y
(
x
)
=
i
sin
x
+
cos
x
{\displaystyle y(x)=i\sin x+\cos x}
d
d
x
(
cos
x
+
i
sin
x
)
=
−
sin
x
+
i
cos
x
=
i
(
i
sin
x
+
cos
x
)
=
i
y
{\displaystyle {\begin{aligned}{\frac {d}{dx}}(\cos x+i\sin x)&=-\sin x+i\cos x\\&=i(i\sin x+\cos x)\\&=iy\end{aligned}}}
使用積分法,可得
i
y
{\displaystyle iy}
y
1
(
x
)
=
e
i
x
+
C
1
{\displaystyle y_{1}(x)=e^{ix}+C_{1}}
y
2
(
x
)
=
cos
x
+
i
sin
x
+
C
2
{\displaystyle y_{2}(x)=\cos x+i\sin x+C_{2}}
其中,
C
1
{\displaystyle \mathbb {C} _{1}}
C
2
{\displaystyle \mathbb {C} _{2}}
又
x
=
0
{\displaystyle x=0}
y
(
0
)
=
1
{\displaystyle y(0)=1}
y
1
(
0
)
=
e
i
0
+
C
1
=
e
0
+
C
1
=
1
+
C
1
{\displaystyle y_{1}(0)=e^{i0}+C_{1}=e^{0}+C_{1}=1+C_{1}}
y
2
(
0
)
=
cos
0
+
i
sin
0
+
C
2
=
1
+
i
(
0
)
+
C
2
=
1
+
C
2
{\displaystyle y_{2}(0)=\cos 0+i\sin 0+C_{2}=1+i(0)+C_{2}=1+C_{2}}
所以
C
1
=
C
2
=
0
{\displaystyle C_{1}=C_{2}=0}
y
(
x
)
=
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle {\begin{aligned}y(x)&=e^{ix}=\cos x+i\sin x\end{aligned}}}
在複分析領域,歐拉公式 亦可以以函數 的形式表示
cis
θ
=
cos
θ
+
i
sin
θ
{\displaystyle \operatorname {cis} \theta =\cos \theta +i\sin \theta }
cis
θ
=
e
i
θ
{\displaystyle \operatorname {cis} \theta =e^{i\theta }}
並且一般定義域 為
θ
∈
R
{\displaystyle \theta \in \mathbb {R} \,}
θ
∈
C
{\displaystyle \theta \in \mathbb {C} \,}
當一複數的模為1,其反函數就是輻角 (arg函數 )。
當
θ
{\displaystyle \theta }
歐拉公式 推廣到更複雜的版本。[ 2]
由於
e
i
α
=
cos
α
+
i
sin
α
{\displaystyle e^{i\alpha }=\cos \alpha +i\sin \alpha }
e
i
β
=
cos
β
+
i
sin
β
{\displaystyle e^{i\beta }=\cos \beta +i\sin \beta }
e
i
(
α
+
β
)
=
cos
(
α
+
β
)
+
i
sin
(
α
+
β
)
=
e
i
α
+
i
β
=
e
i
α
×
e
i
β
=
(
cos
α
+
i
sin
α
)
×
(
cos
β
+
i
sin
β
)
=
(
cos
α
×
cos
β
+
i
sin
α
×
i
sin
β
)
+
(
i
sin
α
×
cos
β
+
cos
α
×
i
sin
β
)
=
(
cos
α
cos
β
−
sin
α
sin
β
)
+
i
(
sin
α
cos
β
+
cos
α
sin
β
)
{\displaystyle {\begin{aligned}e^{i(\alpha +\beta )}&=\cos(\alpha +\beta )+i\sin(\alpha +\beta )=e^{i\alpha +i\beta }\\&=e^{i\alpha }\times e^{i\beta }\\&=(\cos \alpha +i\sin \alpha )\times (\cos \beta +i\sin \beta )\\&=(\cos \alpha \times \cos \beta +i\sin \alpha \times i\sin \beta )+(i\sin \alpha \times \cos \beta +\cos \alpha \times i\sin \beta )\\&=(\cos \alpha \cos \beta -\sin \alpha \sin \beta )+i(\sin \alpha \cos \beta +\cos \alpha \sin \beta )\\\end{aligned}}}
實部等於實部,虛部等於虛部,因此
cos
(
α
+
β
)
=
cos
α
cos
β
−
sin
α
sin
β
{\displaystyle \cos(\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta }
sin
(
α
+
β
)
=
sin
α
cos
β
+
cos
α
sin
β
{\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta }

































![{\displaystyle (1+{\frac {a+bi}{n}})^{n}=[(1+{\frac {a}{n}})+i{\frac {b}{n}}]^{n}=r_{n}(\cos \theta _{n}+i\sin \theta _{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f63eaec548282889f5c49b55ff10badceaa107da)

![{\displaystyle r_{n}=[(1+{\frac {a}{n}})^{2}+({\frac {b}{n}})^{2}]^{\frac {n}{2}},\theta _{n}=n\arctan {\frac {\frac {b}{n}}{1+{\frac {a}{n}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5a1f299e35cc03825493716449af86ca43a7002)
![{\displaystyle {\begin{aligned}\lim _{n\rightarrow \infty }\ln r_{n}&=\lim _{n\rightarrow \infty }[{\frac {n}{2}}\ln(1+{\frac {2a}{n}}+{\frac {a^{2}+b^{2}}{n^{2}}})]\\&=\lim _{n\rightarrow \infty }[{\frac {n}{2}}({\frac {2a}{n}}+{\frac {a^{2}+b^{2}}{n^{2}}})]\\&=a\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e05da47ead760ba5e1035b5f20a9a15e915d40f1)



















![{\displaystyle [a,b]\in I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8af6f338b1689e4c9717e9d5e4a6e89f80c8e775)


































