「
加速 」重新導向至此。關於社會理論,請見「
加速主義 」。
本條目中,向量 與純量 分別用粗體 與斜體 顯示。例如,位置向量通常用
r
{\displaystyle \mathbf {r} \,\!}
r
{\displaystyle r\,\!}
加速度 常見符號
a 國際單位 米每二次方秒 因次
L
T
−
2
{\displaystyle {\mathsf {L}}{\mathsf {T}}^{-2}}
加速度(英語:Acceleration) 是物理學 中的一個物理量,是一個向量 ,主要應用於經典物理 當中,一般用字母
a
{\displaystyle \mathbf {a} }
國際單位制 中的單位為米每二次方秒(
m
/
s
2
{\displaystyle \mathrm {m/s^{2}} }
速度 向量對於時間 的變化率,描述速度的方向和大小變化的快慢。
在經典力學 中,牛頓第二運動定律 說明了力和加速度成正比,這定律又稱為「加速度定律」。假設施加於物體的淨外力為零,則加速度為零,速度為常數,由於動量是質量與速度的乘積,所以動量守恆 。在電動力學 裏,呈加速度運動的帶電粒子 會發射電磁輻射 。
簡單地說,速度 描述了位置是如何變化的,而加速度描述了速度是如何變化的。比如,水平地向前扔出一個物體,起初它的速度朝向正前,然而由於重力 它開始在向前的同時向下墜落,即其速度改變了。這裏改變物體速度的主要是地球的重力 引起的重力加速度 。
加速度具有向量 性質,即需要用大小和方向同時描述一個加速度。在光滑水平面上向前運動的物體,如果向左或向右施以力,即給予了不同的加速度,則其速度會發生變化(包含了速率及方向),然而向左的加速度和向右的加速度顯然引起了不同的效果。同樣,施力的大小不同,引起的加速度不同,最終的結果也不一樣,亦可以從向量的加成性來看。作為一個向量,加速度的疊加和分解分別遵循平行四邊形法則 和三角形法則 。
具體而言,加速度描述的是速度隨時間的變化率。需要注意的是,由於速度也是向量,因此加速度不為零的物體速度的大小(稱之為速率)也不一定會發生變化,實際上,如果加速度保持與速度垂直,速度大小就一直不會改變,同時方向一直改變。這種情況在生活中最常見的是圓周運動,比如在被拴在一端固定的線的另一端的一個小物體在線保持繃直時做的運動,又比如帶電粒子在僅受靜磁場的勞侖茲力
F
=
q
v
×
B
{\displaystyle \mathbf {F} =q\mathbf {v} \times \mathbf {B} }
設質點 A呈一維運動,
t
{\displaystyle t}
x
(
t
)
{\displaystyle x(t)}
Δ
t
{\displaystyle \Delta t}
x
(
t
+
Δ
t
)
{\displaystyle x(t+\Delta t)}
t
{\displaystyle t}
v
(
t
)
=
lim
Δ
t
→
0
x
(
t
+
Δ
t
)
−
x
(
t
)
Δ
t
=
d
x
d
t
{\displaystyle v(t)=\lim _{\Delta t\to 0}{\frac {x(t+\Delta t)-x(t)}{\Delta t}}={\frac {\mathrm {d} x}{\mathrm {d} t}}}
其中,
d
x
d
t
{\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}}
導數 ,在時間-位移圖上表現為求斜率。
首先,定義
t
{\displaystyle t}
t
+
Δ
t
{\displaystyle t+\Delta t}
平均加速度 為
a
¯
=
v
(
t
+
Δ
t
)
−
v
(
t
)
Δ
t
{\displaystyle {\bar {a}}={\frac {v(t+\Delta t)-v(t)}{\Delta t}}}
平均加速度粗略地表示了在該段時間內物體速度的變化情況。如果
Δ
t
{\displaystyle \Delta t}
t
{\displaystyle t}
瞬時加速度 為
a
(
t
)
=
lim
Δ
t
→
0
v
(
t
+
Δ
t
)
−
v
(
t
)
Δ
t
=
d
v
d
t
=
d
2
x
d
t
2
{\displaystyle a(t)=\lim _{\Delta t\to 0}{\frac {v(t+\Delta t)-v(t)}{\Delta t}}={\frac {\mathrm {d} v}{\mathrm {d} t}}={\frac {\mathrm {d^{2}} x}{\mathrm {d} t^{2}}}}
三個質點從坐標原點以相同的速度出發,由於分別擁有正、零、負的加速度而導致其位置和關於時間的曲線。 瞬時加速度,簡稱加速度[ 1] :21 。進而有
v
(
t
1
)
=
∫
t
0
t
1
a
(
t
)
d
t
+
v
(
t
0
)
{\displaystyle v(t_{1})=\int _{t_{0}}^{t_{1}}a(t)\mathrm {d} t+v(t_{0})}
在直線運動時,向量約化為帶符號的純量,其絕對值表示該物理量的大小。速度為正表示向右,速度為負表示向左(二維空間座標中)。加速度與速度方向相同(即符號相同)時表示物體不斷加速,不同則表示物體不斷減速。
右圖畫出了三個質點在
t
=
0
{\displaystyle t=0}
v
0
{\displaystyle v_{0}}
x
{\displaystyle x}
在位移-時間圖上,加速度由曲線的凹凸性 表示,加速度為正的部分表現為凸函數 ,反之為凹函數 ,亦可以從微分的角度來分析。
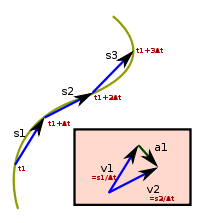
用兩次差分表示如何從位移向量近似地得到加速度向量,在數學表示中以粗體或是上方標註箭號為向量。 設質點A在空間中運動,原點O指向A的向量
r
{\displaystyle \mathbf {r} }
[ 1] :24
v
(
t
)
=
d
r
(
t
)
d
t
{\displaystyle \mathbf {v} (t)={\frac {\mathrm {d} \mathbf {r} (t)}{\mathrm {d} t}}}
a
(
t
)
=
d
v
(
t
)
d
t
=
d
2
r
(
t
)
d
t
2
{\displaystyle \mathbf {a} (t)={\frac {\mathrm {d} \mathbf {v} (t)}{\mathrm {d} t}}={\frac {\mathrm {d^{2}} \mathbf {r} (t)}{\mathrm {d} t^{2}}}}
右圖表現的是一個質點沿一曲線運動的軌跡,表示出了兩次微分的過程,為了清晰表示,這裏使用差分(
Δ
t
{\displaystyle \Delta t}
角速度 )。
在
Δ
t
{\displaystyle \Delta t}
[ 1] :30 。
在經典物理下,即速度遠小於光速、研究宏觀物體時,可以使用伽利略變換 來研究不同參考系間的加速度的聯繫,簡單來說就是座標間的轉換,但仍有保持一定的不變量[ 2] :32 :
a
=
a
′
+
a
rel
{\displaystyle \mathbf {a} =\mathbf {a} '+\mathbf {a} _{\text{rel}}}
其中,
a
{\displaystyle \mathbf {a} }
S
{\displaystyle S}
a
′
{\displaystyle \mathbf {a} '}
S
′
{\displaystyle S'}
a
rel
{\displaystyle \mathbf {a} _{\text{rel}}}
S
′
{\displaystyle S'}
S
{\displaystyle S}
考慮站在地面看火車上的人拋出一個小球,這個公式表達:小球相對於地面的加速度
a
{\displaystyle \mathbf {a} }
a
′
{\displaystyle \mathbf {a} '}
a
rel
{\displaystyle \mathbf {a} _{\text{rel}}}
向量加法 計算。
加速度最主要的應用之一是牛頓第二運動定律。簡單地說,牛頓第二運動定律表明[ 2] :57 ,感受到淨外力的作用,物體的加速度與淨外力成正比,與質量成反比,加速度方向沿淨力方向,在國際單位制中表示為
F
=
m
a
{\displaystyle \mathbf {F} =m\mathbf {a} }
其中
F
{\displaystyle \mathbf {F} }
m
{\displaystyle m}
a
{\displaystyle \mathbf {a} }
在經典物理 下,牛頓第二運動定律廣泛適用。此外,牛頓第二運動定律要求所處參考係為慣性參考系 。由於經典物理的研究幾乎都會或多或少地涉及到物體在力的作用下的運動,又由於牛頓第二運動定律和伽利略變換極具簡潔性,所以,牛頓第二運動定律是經典動力學裏的重要基礎定律,質點運動亦然。
當帶質量物體加速時,慣性 是物體維持原有運動狀態 的傾向,慣性力是對於這傾向的衡量[ 3] 假想力 。更具體而言,根據牛頓第二運動定律,
∑
i
F
i
=
m
a
{\displaystyle \sum _{i}\mathbf {F} _{i}=m\mathbf {a} }
其中,
F
i
{\displaystyle \mathbf {F} _{i}}
i
{\displaystyle i}
a
{\displaystyle \mathbf {a} }
重新編排,可以得到
∑
i
F
i
−
m
a
=
0
{\displaystyle \sum _{i}\mathbf {F} _{i}-m\mathbf {a} =0}
設定慣性向量
I
=
−
m
a
{\displaystyle \mathbf {I} =-m\mathbf {a} }
∑
i
F
+
I
=
0
{\displaystyle \sum _{i}\mathbf {F} +\mathbf {I} =0}
想像這慣性向量為由於加速度運動而產生的一種力,稱為慣性力。因為慣性力與所有作用於這物體的外力的向量總和為零,這動力系統可以視為處於動力平衡狀態。藉着這機制,可以將動力系統約化為靜力系統,用靜力學發展出的方法來解析動力問題[ 3] [ 4] :88ff 。
慣性力在平日生活中其實很常見,例如,停止不動的火車突然向前方加速,則所有站立乘客都會向後方傾移,這便是慣性力效應,從另外一個角度而言也是為了提供乘客們有足夠的摩擦力來進行移動。
將位移對於時間進行一階求導得到了速度,二階求導得到了加速度。可能會想到,可以通過進行三階求導來得到一個諸如加加速度的物理量。
在工程學 中經常需要用到加加速度,特別是在交通工具 設計以及材料等問題[ 5] 加速度 ,也與加加速度有關。在這種情況中,加速度反應人體器官在加速度運動時所感受到的力(見牛頓第二定律 ),加加速度則反應這作用力的變化快慢。較大的加加速度將會使人體產生相當的不適感,例如在電梯 升降,汽車 、火車 等加速和轉彎的過程中(在這些情況中加速度和加加速度的效應一般會同時存在)。人體需要時間適應加速度的變化,假若加加速度超過安全標準,則可能會發生像車禍造成的頸部扭傷 (whiplash)一類的人體傷害。因而在設計交通工具時加加速度是必須考慮的因素。
在物理學裏,加加速度現在主要應用在混沌理論 領域[ 6] [ 7]
角加速度涉及繞着固定軸轉動的物體,例如,想像一個圓盤和一個垂直固定於其中心的木棍,兩隻手合拍住木棍並前後磨擦,造成木棍與圓盤共同轉動(例如,在地上高速旋轉的陀螺 ,繞著固定點轉動)。在圓盤上做一個標記(如一條半徑),則繞着固定軸轉動的物體可以簡單地用純量 角弧 (即該標記轉動的角弧)來做定量描述。
旋轉運動可以與直線運動相類比:位移、速度、加速度,分別對應於角弧、角速度、角加速度。直線運動中已有的定律和方法可以直接帶入,用於旋轉運動,例如,使用已有的勻加速直線運動 理論來研究勻角加速度固定軸轉動[ 2] :249 。
在國際單位制中,角加速度的單位為弧度每二次方秒(
r
a
d
/
s
2
{\displaystyle \mathrm {rad/s^{2}} }
α
(
t
)
=
d
ω
(
t
)
d
t
=
d
2
θ
(
t
)
d
t
2
{\displaystyle \alpha (t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}={\frac {\mathrm {d^{2}} \theta (t)}{\mathrm {d} t^{2}}}}
其中,
α
{\displaystyle \alpha }
ω
{\displaystyle \omega }
角速度 ,
θ
{\displaystyle \theta }
處理關於空間加速度向量的問題,除了直接計算向量之外,更多的時候可以將加速度按照適當坐標軸分解,即將向量形式的加速度表示為相互獨立的不同方向上的純量的形式。因為純量的計算要容易很多,因此這是解決問題常用的方法。
在平面直角坐標系 中,
a
(
t
)
=
a
x
(
t
)
i
+
a
y
(
t
)
j
{\displaystyle \mathbf {a} (t)=a_{x}(t)\mathbf {i} +a_{y}(t)\mathbf {j} }
其中
i
{\displaystyle \mathbf {i} }
j
{\displaystyle \mathbf {j} }
x 、y 坐標軸 上的單位向量 ,皆為常向量。
這種分解方式的優點在於,形式簡便,思維簡單;因為單位向量不會變化,故質點在二個方向上的投影等價於直線運動,並將其疊加,使得問題完全化為代數問題,並且可以直接使用直線運動的已有結論[ 2] :18 。
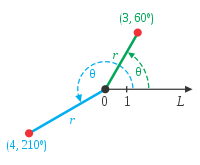
在極點為O、極軸為L的極坐標系裏,點
(
3
,
60
∘
)
{\displaystyle (3,60^{\circ })}
(
4
,
210
∘
)
{\displaystyle (4,210^{\circ })}
在二維空間裏,極坐標系用半徑坐標
r
{\displaystyle r}
θ
{\displaystyle \theta }
單位向量 分別為沿半徑向外的
e
r
{\displaystyle \mathbf {e} _{r}}
e
θ
{\displaystyle \mathbf {e} _{\theta }}
從極坐標
r
{\displaystyle r}
θ
{\displaystyle \theta }
直角坐標 :
x
=
r
cos
θ
{\displaystyle x=r\cos \theta }
y
=
r
sin
θ
{\displaystyle y=r\sin \theta }
在極坐標系中,位置
r
{\displaystyle \mathbf {r} }
v
{\displaystyle \mathbf {v} }
a
{\displaystyle \mathbf {a} }
r
=
r
e
r
{\displaystyle \mathbf {r} =r\mathbf {e} _{r}}
v
=
r
d
θ
d
t
e
θ
+
d
r
d
t
e
r
{\displaystyle \mathbf {v} =r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }+{\frac {dr}{\mathrm {d} t}}\mathbf {e} _{r}}
a
=
[
d
2
r
d
t
2
−
r
(
d
θ
d
t
)
2
]
e
r
+
(
2
d
r
d
t
d
θ
d
t
+
r
d
2
θ
d
t
2
)
e
θ
{\displaystyle \mathbf {a} =\left[{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}-r\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]\mathbf {e} _{r}+\left(2{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right)\mathbf {e} _{\theta }}
兩個單位向量
e
r
{\displaystyle \mathbf {e} _{r}}
e
θ
{\displaystyle \mathbf {e} _{\theta }}
[ 2] :27
d
e
r
=
d
θ
e
θ
{\displaystyle \mathrm {d} \mathbf {e} _{r}=\mathrm {d} \theta \mathbf {e} _{\theta }}
d
e
θ
=
−
d
θ
e
r
{\displaystyle \mathrm {d} \mathbf {e} _{\theta }=-\mathrm {d} \theta \mathbf {e} _{r}}
其中,經過微小時間
d
t
{\displaystyle \mathrm {d} t}
e
r
{\displaystyle \mathbf {e} _{r}}
e
θ
{\displaystyle \mathbf {e} _{\theta }}
d
e
r
{\displaystyle \mathrm {d} \mathbf {e} _{r}}
d
e
θ
{\displaystyle \mathrm {d} \mathbf {e} _{\theta }}
應用微分的萊布尼茲法則
d
d
t
(
a
b
)
=
a
d
b
d
t
+
b
d
a
d
t
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}(a\ b)=a\ {\frac {\mathrm {d} b}{\mathrm {d} t}}+b\ {\frac {\mathrm {d} a}{\mathrm {d} t}}}
在極坐標系下,速度
v
{\displaystyle \mathbf {v} }
a
{\displaystyle \mathbf {a} }
v
=
d
d
t
(
r
e
r
)
=
r
d
θ
d
t
e
θ
+
d
r
d
t
e
r
{\displaystyle {\begin{aligned}\mathbf {v} &={\frac {\mathrm {d} }{\mathrm {d} t}}(r\mathbf {e} _{r})\\&=r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} r}{\mathrm {d} t}}\mathbf {e} _{r}\\\end{aligned}}}
a
=
d
v
d
t
=
d
d
t
(
r
d
θ
d
t
e
θ
)
+
d
d
t
(
d
r
d
t
e
r
)
=
r
d
θ
d
t
d
e
θ
d
t
+
r
d
2
θ
d
t
2
e
θ
+
d
r
d
t
d
θ
d
t
e
θ
+
d
2
r
d
t
2
e
r
+
d
r
d
t
d
e
r
d
t
=
−
r
(
d
θ
d
t
)
2
e
r
+
r
d
2
θ
d
t
2
e
θ
+
d
r
d
t
d
θ
d
t
e
θ
+
d
2
r
d
t
2
e
r
+
d
r
d
t
d
θ
d
t
e
θ
=
[
d
2
r
d
t
2
−
r
(
d
θ
d
t
)
2
]
e
r
+
(
2
d
r
d
t
d
θ
d
t
+
r
d
2
θ
d
t
2
)
e
θ
{\displaystyle {\begin{aligned}\mathbf {a} &={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}\\&={\frac {\mathrm {d} }{\mathrm {d} t}}\left(r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }\right)+{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\mathrm {d} r}{\mathrm {d} t}}\mathbf {e} _{r}\right)\\&=r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {e} _{\theta }}{\mathrm {d} t}}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}\mathbf {e} _{r}+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {e} _{r}}{\mathrm {d} t}}\\&=-r\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\mathbf {e} _{r}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}\mathbf {e} _{r}+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }\\&=\left[{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}-r\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]\mathbf {e} _{r}+\left(2{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right)\mathbf {e} _{\theta }\\\end{aligned}}}
加速度按自然坐標系分解 假設一個質點移動於二維平面。在質點軌道的任意位置,二維自然坐標系的一個坐標軸方向(切向 )保持與軌道切線 方向平行,另一個坐標軸方向(法向 )則與軌道法線 平行。分解按右圖。向量可以無限地做拆解,所以只需要選擇對於分析最有利的為主!通常以切線方向和法線方向來分解。
簡單地說,加速度的切向分量
a
t
{\displaystyle a_{\text{t}}}
a
n
{\displaystyle a_{\text{n}}}
a
t
=
d
v
d
t
{\displaystyle a_{\text{t}}={\frac {\mathrm {d} v}{\mathrm {d} t}}}
a
n
=
v
2
ρ
{\displaystyle a_{\text{n}}={\frac {v^{2}}{\rho }}}
其中,
v
{\displaystyle v}
ρ
{\displaystyle \rho }
[ 2] :24 。
在等速率圓周運動中,速度大小不改變,方向不停改變,需要保持垂直於其切向的加速度來改變方向。 若質點以不變的速率(速度大小)沿着圓周繞着圓心運動,則質點呈等速率圓周運動,質點具有向心加速度
a
n
{\displaystyle \mathbf {a} _{n}}
a
n
=
ω
2
r
=
v
2
r
{\displaystyle a_{\text{n}}=\omega ^{2}r={\frac {v^{2}}{r}}}
其中,
ω
{\displaystyle \omega }
這公式也可以從極坐標系分解中,代入與等速率圓周運動相關的特殊值得到。更一般的情況下(非等速率圓周運動),以向量來表示,
a
n
=
ω
×
(
ω
×
r
)
{\displaystyle \mathbf {a} _{\text{n}}=\mathbf {\omega } \times (\mathbf {\omega } \times \mathbf {r} )}
在向量式中,令沿半徑向外為正。在平面的情況下,該向量式約化為上述純量式,這時會得到一個負號,通常以圓座標來表示最為合適。
假設,在一根繩子的一端系上一個小物體(比如石頭),另一端握在手中,大致保持手不動而水平旋轉,則手會明確地感受到繩子的拉力,該拉力的反作用力在繩子的另一端表現為向心力,提供小物體的向心加速度。當轉得越快,向心力會越大,可以定性地驗證上述向量式。從這個實驗,可以看出,向心加速度總是使物體趨向於朝着圓心做運動;如果沒有繩子施予向心力,物體一定會飛奔出去。
再舉一個例子,在遊樂場的巨大旋轉圓盤上,大部分遊客都會站立不穩,總是會向外摔倒,這是因為缺乏向心力施予於遊客。在旋轉圓盤的非慣性系中,遊客會感受到慣性力 ,但由於缺乏向心力,無法達成平衡狀態,因此被向外「甩」出去[ 4] :96-100 ,這慣性力又稱為離心力 ,人們以這個原理製成了離心機 。
上述公式不但對於從等速率圓周運動成立,也可以應用於各種圓周運動、甚至任意曲線運動,只是上述的
v
{\displaystyle v}
ω
{\displaystyle \omega }
r
{\displaystyle r}
曲率半徑
ρ
{\displaystyle \rho }
如勻速圓周運動圖所示,某一時刻質點速度為
v
1
{\displaystyle \mathbf {v} _{1}}
d
t
{\displaystyle dt}
v
2
{\displaystyle \mathbf {v} _{2}}
v
{\displaystyle v}
r
{\displaystyle r}
β
{\displaystyle \beta }
弧度值 時,速度大小的改變
d
v
{\displaystyle dv}
d
β
{\displaystyle d\beta }
v
d
β
{\displaystyle vd\beta }
[ 2] :23
a
n
=
v
d
β
d
t
=
v
ω
{\displaystyle a_{\text{n}}=v{\frac {\mathrm {d} \beta }{\mathrm {d} t}}=v\omega }
其中,角速度
ω
=
d
β
d
t
{\displaystyle \omega ={\frac {\mathrm {d} \beta }{\mathrm {d} t}}}
以上「近似」在
d
t
→
0
{\displaystyle dt\to 0}
v
=
ω
r
{\displaystyle v=\omega r}
所以,
a
n
=
ω
2
r
=
v
2
r
{\displaystyle a_{\text{n}}=\omega ^{2}r={\frac {v^{2}}{r}}}
氣旋溫斯頓 接近初始峰值強度時的紅外線衛星雲圖。由於科里奧利力影響,風暴以順時針方向旋轉給定固定參考系S 與旋轉參考系S' ,從固定參考系S 觀察,旋轉參考系S' 以勻角速度轉動。移動於旋轉參考系S' 的質點因為運動速度而產生的偏轉效應,稱為「科里奧利效應」,這是為紀念法國科學家賈斯帕-古斯塔夫·科里奧利 而命名。
舉例而言,設想一個巨大的圓盤在地上繞著定點勻角速度轉動(定點運動),而這定點為圓盤的圓心,在圓盤上沿半徑方向有一個直導軌,一個物體被限制在導軌上運動,從圓心勻速向外移動。從地上(固定參考系)觀察,物體的軌跡不是一條直線,而是一條弧形或者螺旋形路線,物體也會感受到導軌的約束力 ,其方向垂直於導軌,並且指向圓盤旋轉方向(不是角速度向量的方向),這約束力促使物體朝着圓盤旋轉方向加速,使物體的軌跡呈弧形或螺旋形。從圓盤(旋轉坐標系)觀察,物體所感受到的科里奧利力會與導軌施予的約束力相抵消,因此,物體只會呈直線運動。假若,導軌不存在,則物體會逆着圓盤旋轉方向以科里奧利加速度運動。
在科里奧利效應裏,參考系S'的物體的柯里奧利加速度與感受到的科里奧利力分別為[ 4] :100-103
a
cor
=
−
2
Ω
×
v
{\displaystyle \mathbf {a} _{\text{cor}}=-2{\boldsymbol {\Omega }}\times \mathbf {v} }
F
cor
=
−
2
m
Ω
×
v
{\displaystyle \mathbf {F} _{\text{cor}}=-2m{\boldsymbol {\Omega }}\times \mathbf {v} }
其中
a
cor
{\displaystyle \mathbf {a} _{\text{cor}}}
Ω
{\displaystyle {\boldsymbol {\Omega }}}
角速度向量 ,
v
{\displaystyle \mathbf {v} }
S' 中的速度向量。
在氣象學 裏,科里奧利力使得熱帶氣旋 在沒有強引導氣流 影響下移向兩極[ 8] 兩極 部分含有東風,科里奧利力會將東風拉向兩極;靠近赤道部分含有西風,科里奧利力會將西風拉向赤道。在地球上越接近赤道科里奧利力會越弱,所以科里奧利力影響熱帶氣旋靠近兩極部分會較靠近赤道部分為多。因此,在沒有其他引導氣流抵消科里奧利力的情況下,北半球的熱帶氣旋一般會向北移動,而南半球的熱帶氣旋則會向南移動[ 9]
科里奧利力也會開啟氣旋系統的旋轉,但驅動高速度旋轉的主要因素,不是科里奧利力,而是凝結熱 [ 10]
給定固定參考系S 與旋轉參考系S' ,從固定參考系S 觀察,旋轉參考系S' 以非勻角速度
Ω
{\displaystyle {\boldsymbol {\Omega }}}
S' 觀察,物體因這非勻角速度而感受到的虛設力 (fictitious force)稱為「歐拉力」,產生的加速度稱為「歐拉加速度」。歐拉力
F
Euler
{\displaystyle \mathbf {F} _{\text{Euler}}}
a
Euler
{\displaystyle \mathbf {a} _{\text{Euler}}}
F
Euler
=
m
a
Euler
{\displaystyle \mathbf {F} _{\text{Euler}}=m\mathbf {a} _{\text{Euler}}}
設想一個巨大的圓盤在地上繞著定點轉動,而這定點為圓盤的圓心。在圓盤的非圓心位置固定一個物體。圓盤呈非勻角速度運動,則從旋轉參考系S'觀察,延著物體的圓形軌跡切向(不是角速度向量的方向),此物體的受力是歐拉力。
歐拉加速度的一般公式為[ 4] :100-103
a
Euler
=
−
d
Ω
d
t
×
r
{\displaystyle \mathbf {a} _{\text{Euler}}=-{\frac {\mathrm {d} {\boldsymbol {\Omega }}}{\mathrm {d} t}}\times \mathbf {r} }
其中,
r
{\displaystyle \mathbf {r} }
歐拉力為[ 4] :100-103
F
Euler
=
−
m
d
Ω
d
t
×
r
{\displaystyle \mathbf {F} _{\text{Euler}}=-m{\frac {\mathrm {d} \mathbf {\Omega } }{\mathrm {d} t}}\times \mathbf {r} }
以下為幾種特殊的運動,因為在不同的模型下質點常被不同地近似處理,並且可以得出的結論較之上面的積分式常能極大地簡省計算量,故有研究的價值。最常運用的就是拋體運動,以及自由落體。
若某質點保持加速度
a
=
0
{\displaystyle a=0\,\!}
v
{\displaystyle \mathbf {v} \,\!}
v
=
0
{\displaystyle v=0\,\!}
勻速直線運動主要出現在牛頓第一運動定律 中,該定律表示:「不受任何力或受淨力為零的物體作勻速直線運動。」由於自然界中大部分力 的隨距離增大而減小,故離所有其它物體足夠遠的某一物體的運動能夠在足夠的精度 下被近似為勻速直線運動。這種近似常被用於尋找慣性參考系 和粒子物理學 的運算當中。
位於喬治亞州的六旗主題公園的自由落體機,從高達數十米的地方由靜止釋放,長長的途中幾乎只受到重力,近似為自由落體運動,使得乘客落到地面附近時擁有極高的速度。 若某作質點作直線運動並保持加速度
a
{\displaystyle a\,\!}
t
=
0
{\displaystyle t=0\,\!}
v
0
{\displaystyle v_{0}\,\!}
t
{\displaystyle t\,\!}
v
(
t
)
{\displaystyle v(t)\,\!}
位移 為
s
(
x
)
{\displaystyle s(x)\,\!}
v
(
t
)
=
v
0
+
a
t
.
{\displaystyle v(t)=v_{0}+at\,.}
s
(
t
)
=
v
0
t
+
1
2
a
t
2
=
v
(
t
)
+
v
0
2
t
{\displaystyle {\begin{aligned}s(t)&=v_{0}t+{\frac {1}{2}}at^{2}\\&={\frac {v(t)+v_{0}}{2}}t\\\end{aligned}}}
以及得出
a
=
v
(
t
)
2
−
v
0
2
2
s
(
t
)
{\displaystyle a={\frac {v(t)^{2}-v_{0}^{2}}{2s(t)}}}
自由落體運動是指初速度為0,加速度恆為豎直向下
[ 11] 重力加速度 g的運動,在地球上大約有
g
=
9.8
m
⋅
s
-
2
{\displaystyle g=9.8\operatorname {m\cdot s^{-2}} }
[ 12] 空氣阻力 遠小於其重力 時,在一定精度內可被視作自由落體運動。
加速度是一個向量,因此「加速度恆定」暗示加速度的大小和方向都不隨時間變化。
一個從左向右被拋出的籃球是如何在重力下運動的(拋體運動)。相鄰兩個球影之間有相同的時間間隔。 當加速度
a
{\displaystyle \mathbf {a} \,}
v
{\displaystyle \mathbf {v} \,}
平面直角坐標系 分解,使質點的運動在其中一個坐標軸上的投影為勻速直線運動,另一個方向上為勻變速直線運動。根據獨立作用原理 ,兩者的合運動(即質點的軌跡)為一條拋物線的一部分。
拋體運動具體包括平拋運動和斜(上、下)拋運動,和自由落體運動類似,它是在地球上向不同方向拋出的物體在忽略空氣阻力的情況下的運動狀況進行理想化的抽象模型。物體擁有一個非豎直方向的不為零初速度
v
0
{\displaystyle \mathbf {v_{0}} \,\!}
再一個例子是簡諧運動,即質點在正弦或餘弦函數形式下的一維運動,一般形式為
x
=
A
cos
(
ω
t
+
ϕ
0
)
.
{\displaystyle x=A\cos(\omega t+\phi _{0})\,.}
其中,
A
{\displaystyle A\,}
ω
{\displaystyle \omega \,}
ϕ
0
{\displaystyle \phi _{0}\,}
v
=
−
A
ω
sin
(
ω
t
+
ϕ
0
)
{\displaystyle v=-A\omega \sin(\omega t+\phi _{0})\,}
a
=
−
A
ω
2
cos
(
ω
t
+
ϕ
0
)
{\displaystyle a=-A\omega ^{2}\cos(\omega t+\phi _{0})}
由此也可以得出一些有趣的結論,如在任一時刻,
a
=
−
x
ω
2
{\displaystyle a=-x\omega ^{2}\,}
A
2
=
(
a
ω
2
)
2
+
(
v
ω
)
2
{\displaystyle A^{2}=\left({\frac {a}{\omega ^{2}}}\right)^{2}+\left({\frac {v}{\omega }}\right)^{2}\,}
加速度的另一個重要應用之處是帶電粒子的電磁輻射(即手機和收音機使用所需要的信號來源)。通過對麥克斯韋方程組 的研究,可以將帶電粒子產生電磁輻射的規律概括性地定性總結為:帶電粒子的加速度產生電磁輻射,並且電磁輻射的強度和加速度大小正相關[ 13] 粒子對撞機 中,帶電粒子以很高的速度運動,經受撞擊後變慢、靜止甚至反彈回來,這個過程中顯然速度發生劇烈改變,一定經受了加速度不為零的過程,也一定會放出輻射。這樣產生的輻射被稱為軔致輻射 。
加速度產生電磁輻射的另一個很典型的例子是迴旋加速器(迴旋輻射 )。帶電粒子在迴旋加速器中作圓周運動,每半圈加速一次,同時運動半徑增大從而形成螺旋軌道,最後以很高的速度射出。圓周運動需要向心加速度來維持,當速度相當高時,加速度太大以至於因為電磁輻射損失的能量過多,導致迴旋加速器實際對粒子的加速作用有上限。光速可比擬時,這時因為相對論效應而需使用同步加速器 。這樣產生的光能量高、偏振高,並且集中在一個很小的錐角里(相對論效應導致的前燈效應 ),因此是很好的大型物理用同步輻射光源 。
狹義相對論 用於速度可以和光速 相比擬時的運動,並且要求參考系是慣性系 。在狹義相對論中,加速度的定義沒有改變。然而,由於在狹義相對論中,不同的參考系有不同的時間和空間度量標準,即當前參考系中的加速度為當前 參考系中的位移對當前 參考系中的時間的二階導數,因此在參考系變換(勞侖茲變換 )時變得複雜很多。
設有兩個參考系
S
{\displaystyle S}
S
′
{\displaystyle S'}
t
=
t
′
=
0
{\displaystyle t=t'=0}
S
{\displaystyle S}
S
′
{\displaystyle S'}
v
{\displaystyle v}
x 正方向運動。
同一事件在兩個參考系中的時空坐標
(
x
,
y
,
z
,
t
)
{\displaystyle (x,y,z,t)}
(
x
′
,
y
′
,
z
′
,
t
′
)
{\displaystyle (x',y',z',t')}
{
x
=
γ
(
x
′
+
v
t
)
y
=
y
′
z
=
z
′
t
=
γ
(
t
′
+
v
c
2
x
)
{\displaystyle {\begin{cases}x=\gamma (x'+vt)\\y=y'\\z=z'\\t=\gamma \left(t'+{\cfrac {v}{c^{2}}}x\right)\\\end{cases}}}
其中,單撇符號
′
{\displaystyle '}
S
′
{\displaystyle S'}
γ
=
1
1
−
v
2
c
2
{\displaystyle \gamma ={\tfrac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}
勞侖茲因子 ,用
(
u
x
,
u
y
,
u
z
)
{\displaystyle \left(u_{x},u_{y},u_{z}\right)}
(
a
x
,
a
y
,
a
z
)
{\displaystyle \left(a_{x},a_{y},a_{z}\right)}
{
d
x
d
t
=
u
x
d
u
x
d
t
=
a
x
{\displaystyle {\begin{cases}{\cfrac {\mathrm {d} x}{\mathrm {d} t}}=u_{x}\\{\cfrac {\mathrm {d} u_{x}}{\mathrm {d} t}}=a_{x}\end{cases}}}
y、z方向的定義式與之類似。綜合該定義式,利用坐標轉換的t部分,將坐標轉換的x、y、z連續兩次進行一階求導[ 2] :501 。
通過展開,可以得到[ 14]
{
a
x
=
a
x
′
γ
3
(
1
+
v
u
x
′
c
2
)
3
a
y
=
1
γ
2
[
a
y
′
(
1
+
v
u
x
′
c
2
)
2
−
v
u
y
′
c
2
a
x
′
(
1
+
v
u
x
′
c
2
)
3
]
a
z
=
1
γ
2
[
a
z
′
(
1
+
v
u
x
′
c
2
)
2
−
v
u
z
′
c
2
a
x
′
(
1
+
v
u
x
′
c
2
)
3
]
{\displaystyle {\begin{cases}a_{x}={\cfrac {a'_{x}}{\gamma ^{3}\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{3}}}\\a_{y}={\cfrac {1}{\gamma ^{2}}}\left[{\cfrac {a'_{y}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{2}}}-{\cfrac {{\frac {vu'_{y}}{c^{2}}}a'_{x}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{3}}}\right]\\a_{z}={\cfrac {1}{\gamma ^{2}}}\left[{\cfrac {a'_{z}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{2}}}-{\cfrac {{\frac {vu'_{z}}{c^{2}}}a'_{x}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{3}}}\right]\\\end{cases}}}
假想實驗:站在兩種封閉電梯廂中兩個人,無法分辨球的加速度是由慣性力還是真正的重力施加的。 其中,
γ
=
1
/
1
−
v
2
/
c
2
{\displaystyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}}
勞侖茲因子 。
可以看出,在狹義相對論中,加速度的變換公式冗長而複雜,各分量的公式也極不相似。再加上如果要考慮到力,雖然
F
=
m
a
{\displaystyle \mathbf {F} =m\mathbf {a} }
張量分析 [ 2] :501 。
在廣義相對論中和在量子力學中,大都是從能量、動量等的角度出發(類似於分析力學 ),而很少會像牛頓第二運動定律一樣涉及到作用力;實際上,即使在需要表示出「位移的二階導數」這一個量的時候,會趨向於直接使用
x
¨
{\displaystyle {\ddot {x}}}
d
2
x
d
t
2
{\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}}
微分方程式 。因此,加速度在進階理論中較少被用到。
運用到加速度的其中一個例子是等效原理 ,簡單地說[ 2] :523 ,它敘述了觀測者不能在局部的區域內分辨出由加速度所產生的慣性力或由物體所產生的重力。比如,觀測者站在地球上靜止的電梯廂中向前方拋球,球會向下墜落,是因為地球的重力 ;而在遠離任何星體的宇宙中的一個電梯廂,在以重力加速度
g
{\displaystyle g}
慣性力 。作為在封閉電梯廂中的觀測者無法分辨這兩種情況,愛因斯坦據此提出,重力與慣性力等價。等效原理是廣義相對論中的支柱性原理之一。
^ 1.0 1.1 1.2 趙凱華,羅蔚茵. 《新概念物理教程·力学(第二版)》. 北京: 高等教育出版社. 2004. ISBN 7-04-015201-0 ^ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 鄭永令,賈起民,方小敏. 《力学(第二版)》. 北京: 高等教育出版社. 2002. ISBN 978-7-04-011084-5 ^ 3.0 3.1 Beer, Ferdinand; Johnston, Jr., E. Russ, Vector Mechanics for Engineers:dynamics 7th: pp. 699, 2004, ISBN 978-0-072-93079-5 ^ 4.0 4.1 4.2 4.3 4.4 Lanczos, Cornelius, The Variational Principles of Mechanics, Dovers Publications, Inc, 1970, ISBN 978-0-486-65067-8 ^ 存档副本 . [2013-02-19 ] . (原始內容存檔 於2013-05-18). ^ 黃沛天,馬善鈞,徐學翔,胡利雲.變加速動力學縱橫,2010年7月5日查詢
^ Sprott JC. Some simple chaotic jerk functions (PDF) . Am J Phys. 1997, 65 (6): 537–43 [2009-09-28 ] . Bibcode:1997AmJPh..65..537S doi:10.1119/1.18585 原始內容 (PDF) 存檔於2010-06-13). ^ Baum, Steven K ,1997年1月20日,The Glossary: Cn-Cz.. Glossary of Oceanography and the Related Geosciences with References. Texas A&M University(英文) ^ Tropical cyclone: Tropical cyclone tracks. . Encyclopædia Britannica . 2008-02-25 [2009-05-07 ] . (原始內容存檔 於2012-06-22). ^ NOAA FAQ: How much energy does a hurricane release? . National Oceanic & Atmospheric Administration. August 2001 [2009-06-30 ] . (原始內容存檔 於2017-11-02). ^ 豎直向下 ,又稱鉛直向下 ,被定義為重力加速度的方向。但其具體方向因重力加速度的兩種定義不同而異,分別為指向地心 和與緯度有關 ,參見萬有引力#兩者的微妙差別 。^ g在不同地區稍有不同,並且g有兩種不同的定義(見上一條註釋)。一般需要更精確的計算中g可近似的取作標準重力加速度,即g=gn =9.80665 ms-2 ,這個值是已經包括了和地球自轉的向心力的。該數值來自氣象港,http://qxg.com.cn/n/?cid=44&nid=764&fc=nd,2010年5月18日查阅。 (頁面存檔備份 ,存於互聯網檔案館 )
^ 這裏並沒有用到準確的物理術語。準確地說,是輻射的能流密度 與粒子加速度的平方成正比。趙凱華,陳熙謀. 《新概念物理教程·电磁学》. 北京: 高等教育出版社. 2003: pp.417–419. ISBN 7-04-011693-6
^ French, Anthony, Special Relativity (Mit Introductory Physics Series), United States of America: W. W. Norton: pp. 153–154, 1968, ISBN 978-0748764228(英語)
線性(平動)的量
角度(轉動)的量
因次
—
L
L2
因次
—
—
—
T
時間 : t s 位移積分 : A m s T
時間 : t s
—
距離 : d 位矢 : r s x 位移 m 面積 : A m2 —
角度 : θ 角移 : θ rad 立體角 : Ω rad2 , sr
T−1
頻率 : f s−1 Hz 速率 : v 速度 : v m s−1 面積速率 : ν m2 s−1 T−1
頻率 : f s−1 Hz 角速率 : ω 角速度 : ω rad s−1
T−2
加速度 : a m s−2 T−2
角加速度 : α s−2
T−3
加加速度 : j −3 T−3
角加加速度 : ζ s−3
M
質量 : m kg ML2
轉動慣量 : I m2
MT−1
動量 : p 衝量 : J m s−1 , N s 作用量 : 𝒮 actergy : ℵ m2 s−1 , J s ML2 T−1
角動量 : L 角衝量 : ι m2 s−1 作用量 : 𝒮 actergy : ℵ m2 s−1 , J s
MT−2
力 : F 重量 : F g kg m s−2 , N 能量 : E 功 : W kg m2 s−2 , J ML2 T−2
力矩 : τ moment M kg m2 s−2 , N m 能量 : E 功 : W kg m2 s−2 , J
MT−3
加力 : Y kg m s−3 , N s−1 功率 : P kg m2 s−3 , W ML2 T−3
rotatum P kg m2 s−3 , N m s−1 功率 : P kg m2 s−3 , W































































![{\displaystyle \mathbf {a} =\left[{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}-r\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]\mathbf {e} _{r}+\left(2{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right)\mathbf {e} _{\theta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87eee0bf811b2a68b0ee5d7a131c966427daf7d8)







![{\displaystyle {\begin{aligned}\mathbf {a} &={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}\\&={\frac {\mathrm {d} }{\mathrm {d} t}}\left(r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }\right)+{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\mathrm {d} r}{\mathrm {d} t}}\mathbf {e} _{r}\right)\\&=r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {e} _{\theta }}{\mathrm {d} t}}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}\mathbf {e} _{r}+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {e} _{r}}{\mathrm {d} t}}\\&=-r\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\mathbf {e} _{r}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }+{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}\mathbf {e} _{r}+{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {e} _{\theta }\\&=\left[{\frac {\mathrm {d} ^{2}r}{\mathrm {d} t^{2}}}-r\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]\mathbf {e} _{r}+\left(2{\frac {\mathrm {d} r}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+r{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right)\mathbf {e} _{\theta }\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27510f25b4ac9bdfb43ff0a70fb7f164c36b99fe)






























































![{\displaystyle {\begin{cases}a_{x}={\cfrac {a'_{x}}{\gamma ^{3}\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{3}}}\\a_{y}={\cfrac {1}{\gamma ^{2}}}\left[{\cfrac {a'_{y}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{2}}}-{\cfrac {{\frac {vu'_{y}}{c^{2}}}a'_{x}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{3}}}\right]\\a_{z}={\cfrac {1}{\gamma ^{2}}}\left[{\cfrac {a'_{z}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{2}}}-{\cfrac {{\frac {vu'_{z}}{c^{2}}}a'_{x}}{\left(1+{\frac {vu'_{x}}{c^{2}}}\right)^{3}}}\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8198c2635d3862c19606b42d1bb6e445756a49e)



