函数

在数学领域，函数是一种关系，这种关系使一个集合里的每一个元素对应到另一个（可能相同的）集合里的唯一元素。函数的概念对于数学和数量学的每一个分支来说都是最基础的。

术语函数，映射，对应，变换通常都是同一个意思。

概述

简而言之，函数是将唯一的输出值赋予每一输入的“法则”。这一“法则”可以用函数表达式、数学关系，或者一个将输入值与输出值对应列出的简单表格来表示。函数最重要的性质是其决定性，即同一输入总是对应同一输出（注意，反之未必成立）。从这种视角，可以将函数看作“机器”或者“黑盒”，它将有效的输入值变换为唯一的输出值。通常将输入值称作函数的参数，将输出值称作函数的值。

最常见的函数的参数和函数值都是数，其对应关系用函数式表示，函数值可以通过直接将参数值代入函数式得到。如下例，

f(x)=x^{2}

，x 的平方即是函数值。

也可以将函数很简单的推广到与多个参量相关的情况。例如：

g(x,y)=xy

有两个参量x和y，以乘积xy为值。与前面不同，这一“法则”与两个输入相关。其实，可以将这两个输入看作一个有序对(x, y），记g为以这个有序对(x, y）作参数的函数，这个函数的值是xy。

科学研究中经常出现未知或不能给出表达式的函数。例如地球上不同时刻温度的分布，这一函数以地点和时间为参量，以某一地点、某一时刻的温度作为输出。

函数的概念并不局限于数的计算，甚至也不局限于计算。函数的数学概念更为宽泛，而且不仅仅包括数之间的映射关系。函数将“定义域”（输入集）与“对映域”（可能输出集）联系起来，使得定义域的每一个元素都唯一对应对映域中的一个元素。函数，如下文所述，被抽象定义为确定的数学关系。由于函数定义的一般性，函数概念对于几乎所有的数学分支都是很基本的。

历史

函数这个数学名词是莱布尼兹在1694年开始使用的，以描述曲线的一个相关量，如曲线的斜率或者曲线上的某一点。莱布尼兹所指的函数现在被称作可导函数，数学家之外的普通人一般接触到的函数即属此类。对于可导函数可以讨论它的极限和导数。此两者描述了函数输出值的变化同输入值变化的关系，是微积分学的基础。

1718年，约翰·贝努里（en:Johann Bernoulli）把函数定义为“一个变量的函数是指由这个变量和常量以任何一种方式组成的一种量。”1748年，约翰·贝努里的学生欧拉（Leonhard Euler）在《无穷分析引论》一书中说：“一个变量的函数是由该变量和一些数或[常量]]以任何一种方式构成的解析表达式”。例如f(x) = sin(x) + x³。1775年，欧拉在《微分学原理》一书中又提出了函数的一个定义：“如果某些量以如下方式依赖于另一些量，即当后者变化时，前者本身也发生变化，则称前一些量是后一些量的函数。”

19世纪的数学家开始对数学的各个分支作规范整理。维尔斯特拉斯（Karl Weierstrass）提出将微积分学建立在算术，而不是几何的基础上，因而更趋向于欧拉的定义。

通过扩展函数的定义，数学家能够对一些“奇怪”的数学对象进行研究，例如不可导的连续函数。这些函数曾经被认为只具有理论价值，迟至20世纪初时它们仍被视作“怪物”。稍后，人们发现这些函数在对如布朗运动之类的物理现象进行建模时有重要的作用。

到19世纪末，数学家开始尝试利用集合论来规范数学。他们试图将每一类数学对象定义为一个集合。狄利克雷（Johann Peter Gustav Lejeune Dirichlet）给出了现代正式的函数定义（参见下文#正式定义）。狄利克雷的定义将函数视作数学关系的特例。然而对于实际应用的情况，现代定义和欧拉定义的区别可以忽略不计。

正式定义

从输入值集合X 到可能的输出值集合Y 的函数f（记作 f : X → Y）是X与Y的关系，满足如下条件：

f 是完全的：对X 中任一元素x 都有集合Y 中的元素y 满足x f y （x 与y 是f 相关的）。即，对每一个输入值，Y 中都有至少一个与之对应的输出值。
f 是多对一 的：若x f y 且x f z ，则y = z 。即，多个输入可以映射到一个输出，但一个输入不能映射到多个输出。

定义域中任一x 在对映域中唯一对应的y 记为f(x)。

比上面定义更简明的表述如下：从X 映射到Y 的函数f 是X 与Y 的直积X × Y 的子集。X 中任一x 都与Y 中的y 唯一对应，且有序对(x, y)属于f 。

X与Y的关系若满足条件(1)，则为多值函数。函数都是多值函数，但多值函数不都是函数。X与Y的关系若满足条件(2)，则为部分函数。函数都是部分函数，但部分函数不都是函数。除非特别指明，本百科全书中的“函数”总是指同时满足以上两个条件的关系。

考虑如下例子：

File:NotMap1.png	完全，但非多对一。X中的元素3与Y中的两个元素b 和c 相关。因此这是多值函数，但不是函数。
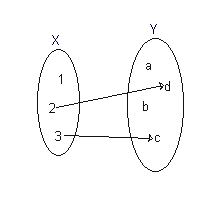
	多对一，但非完全。 X 的元素1未与Y 的任一元素相关。因此这是部分函数，但不是函数。
File:Mathmap2.png	完全且多对一。因此这是从X到Y的函数。此函数可以表示为f ={(1, d), (2, d), (3, c)}，或 $f(x)=\left\{{\begin{matrix}d,&{\mbox{if }}x=1\\d,&{\mbox{if }}x=2\\c,&{\mbox{if }}x=3.\end{matrix}}\right.$

定义域、对映域和值域

输入值的集合X被称为f 的定义域；可能的输出值的集合Y被称为f 的陪域。函数的值域是指定义域中全部元素通过映射f 得到的实际输出值的集合。注意，把对映域称作值域是不正确的，函数的值域是函数的对映域的子集。

计算机科学中，参数和返回值的数据类型分别确定了子程序的定义域和对映域。因此定义域和对映域是函数一开始就确定的强制约束。另一方面，值域和实际的实现有关。

內射、满射与双射函数

內射函数，将不同的变量映射到不同的值。即：若x和y属于定义域，则仅当x = y时有f(x) = f(y)。
满射函数，其值域即为其对映域。即：对映射f的对映域中之任意y，都存在至少一个x满足f(x) = y。
双射函数，既是单射的又是满射的。也叫一一对应。双射函数经常被用于表明集合X和Y是等势的，即有一样的基数。如果在两个集合之间可以建立一个一一对应，则说这两个集合等势。

像和原象

元素 x∈X在 f 的像就是 f(x)。

子集 A⊂X 在 f 的像是以其元素的像組成 Y的子集，即

f(A) := {f(x) : x ∈ A}。

注意 f 的值域就是定義域 X 的像 f(X)。在我們的例子裡， {2,3} 在 f 的像是 f({2, 3}) = {c, d} 而 f 的值域是 {a, c, d}。

根據此定義，f 可引申成為由 X 的能集（由 X 的子集組成的集）到 Y 的能集之函數，冲，亦記作 f。

子集 B ⊂ Y 在 f 的原像（或逆像）是如下定義 X的子集：

f⁻¹(B) := {x ∈ X : f(x)∈B}。

在我們的例子裡，{a, b} 的原像是 f⁻¹({a, b}) = {1}。

根據此定義，f⁻¹ 是由 Y 的能集到 X 的能集之函數。

以下是 f 及 f⁻¹ 的一些特性：

f(A₁ ∪ A₂) = f(A₁) ∪ f(A₂).
f(A₁ ∩ A₂) ⊆ f(A₁) ∩ f(A₂).
f⁻¹(B₁ ∪ B₂) = f⁻¹(B₁) ∪ f⁻¹(B₂).
f⁻¹(B₁ ∩ B₂) = f⁻¹(B₁) ∩ f⁻¹(B₂).
f(f⁻¹(B)) ⊆ B.
f⁻¹(f(A)) ⊇ A.

這些特性適合定義域的任意子集 A, A₁ 及 A₂ 和輸出值域的任意子集 B, B₁ 及 B₂，甚至可推廣到任意子集群的交集和並集。

函数图像

File:225px-Cubicpoly.png

立方函数的图像

函数f 的图像是平面上点对(x,f(x))的集合，其中x取定义域上所有成员的。函数图像可以帮助理解证明一些定理。

如果X 和Y 都是连续的线，则函数的图像有很直观表示，如右图是立方函数的图像：

注意两个集合X 和Y 的二元关系有兩個定義：一是三元組(X,Y,G)，其中G 是關係的圖；二是索性以關係的圖定義。用第二個定義則函数 f 等於其图象。

函数例子

(详见函数列表.)

某一特定时刻在中国每一人口与其体重之关系「wght」。
每个国家与其首都之关系（若不把多首都国[1]计算在内)。
每个自然数 n 与其平方 n² 之关系「sqr」。
每个正实数 x 与其自然对数 ln x 之关系「ln」。注意，对于所有实数 x，ln 其实不是一个函数，因为并不是所有实数在 ln 里都有定义，即是 ln 不是完全 (total) 的。
每个在 $\mathbb {R} ^{2}$ 平面上的点与其和原点 (0, 0) 的距离之关系「dist」
每个在 $\mathbb {R} ^{2}\setminus \{(0,0)\}$ 有孔平面 (Puntured plane) 上的点与描述该点受到原点发出的引力的矢量。

最常用的数学函数包括加法、减法、乘法、除法、冪、对数、根号、多项式、有理函数、三角函数等。它们统称为「初等函数」-- 但此名的定义会随使用的数学分支而改变。非初等函数（或特殊函数）包括 Bessel函数和伽傌函數。

函數的特性

函數可分為

歧義函數

歧義函數指可於一條數學等式中找到不少於一個正確答案。例如，4的平方根可以是2或者-2而兩者的平方皆是4。

嚴格來說，歧義函數不完全算是函數，因為數學函數的定義對於一個輸入值只能有唯一一個輸出值。實際上，這樣的「函數」通常被稱為關係式。

大陆的名称叫多值函数

n-元函数: 多元函数

n-元函數是指輸入值為 n-元組的函數。或者說，若一函數的輸入值域為 n 個集合的積集的子集，這函數就是 n-元函數。例如, 距離函數 dist((x,y)) 是一個二元函數，輸入值是由兩個點組成的序對。另外，多複變函數（即輸入值為複數的多元組）是一個重要的數學課題。

在抽象代數中, 運算元其實都是函數，如乘法 "*" 是個二元函數：我們寫 x*y 其實是 *(x,y)的中綴表達法。

函數式程序设计是一個以函數概念為中心的重要理論範例，其中的运算对象为多元函数，基本语法基于λ演算，而函数的复合（见下）则采用代换来完成。特别地，通过一种称为Currying的变换，可将多元函数变换为一元函数。

复合函数

函數 f: X → Y 及 g: Y → Z 的複合函數是

g o f: X → Z :(g o f)(x) = g(f(x))。

舉例, 飛機在 t 时刻的高度是 h(t)，而高度 x 处的氧气浓度是 c(x)，則在 t 时刻飛機周围的氧氣濃度是 (c o h)(t)。

若 Y⊂X 則 f 可自我複合; 此時複合函數可記作 f²（不要與三角學的符號混淆）。函數的幂的定義是對自然數 n 有

fⁿ⁺¹= fⁿ o f= f ofⁿ。

反函数

对一个函数 f:X→Y ，若值域 Y 中任何一个元素 y 的原象是唯一的，那么这个函数就被称为是双射的。对任意的 y∈Y 到它的原象f⁻¹(y)的映射，我们称之为 f 的反函数，记为 f⁻¹。

举一个反函数的例子，比如 f(x) = x² ，它的反函数是 f(x)⁻¹ = √x 。[啊恩！...你必须指明它的定义域是...如果你说定义域是R，那就错了]同样，2x 的反函数是 x/2。反函数是一个函数，它能够“抵消”它的原函数。参见逆映射。

限制及擴張

給出 $Y$ 的子集 $X$ 以及函數

f:Y\rightarrow Z

，

則

f|X:X\rightarrow Y

f|X(x)=f(x)

稱為 $f$ 在 $X$ 的限制。

反之，若給出函數

g:X\to Z

則一個定義在 $Y$ 的函數 $f:Y\to Z$ 適合 $f|X=g$ ，就是 $g$ 的擴張。

点态运算

設函數 f: X → R 及g: X → R 有 X 為共同的輸入值域及環 R 為共同輸出值域。我們可以定義函數和 f + g: X → R 及函數積 f × g: X → R 如下:

(f + g)(x) := f(x) + g(x);

(f × g)(x) := f(x) × g(x);

for all x in X。

這樣子我們得出一個函數組成的環。這是一個抽象性擴張的例子，由此我們由較簡單的結構得出更複雜的。

若然以抽象代數 A 代替 R, 得出的由 X 到 A 的函數集會類似地擁有和 A 相同的代數結構。

可计算和不可计算函数

所有从整数到整数的可计算函数的个数是可数的，这是因为所有可能的算法个数是可数的。从整数到整数的函数个数要更多些－和实数个数一样多，也就是说是等势的。这说明有些从整数到整数的函数是不可计算的。关于不可计算函数，请参看停机问题和莱斯定理。

范畴学中的函数

函數定義為定义域X與上域Y的關係。而在范畴学中，函数的槪念被擴張成射的槪念。一個范畴包括一組物件與一組射，每一個射是個有序三元组(X, Y, f)，其中f是从定义域X到上域Y的一個關係，而定义域与上域是范畴內的物件。基于这种解释，可以把函数看作集合范畴里面的射。

参见

*Visual Calculus by Lawrence S. Husch, University of Tennessee (2001)

外部连接

Wolfram函数网站，汇集了各数学函数的公式和图像

xFunctions 一个多功能的Java小程序，可以显示函数的图像，既可以在线使用，也可以下载运行。