冪

幂（汉语拼音：mì，注音：ㄇㄧˋ，音同“覓”），指乘方运算的结果。$n^m$指將$n$自乘$m$次。把$n^m$看作乘方的结果，叫做「n的m次幂」或「n的m次方」。

$n^m = \underbrace{n \times \cdots \times n}_m$

其中，n稱為「底數」，m稱為「指數」（寫成上標）。當不能用上標時，例如在編程語言或電子郵件中，$n^m$通常寫成n^m或n**m，亦可以用高德納箭號表示法，寫成n↑m，讀作“n的m次方”。

當指數為1時，通常不寫出來，因為運算出的值和底數的數值一樣；指數為2時，可以讀作“n的平方”；指數為3時，可以讀作“n的立方”。

n^m的意義亦可視為

$n^m = 1\times \underbrace{n \times \cdots \times n}_m$

起始值1（乘法的單位元）乘上底數（n）自乘指數（m）這麼多次。這樣定義了後，很易想到如何一般化指數0和負數的情況：除0外所有數的零次方都是1；指數是負數時就等於重複除以底數（或底數的倒數自乘指數這麼多次），即：

$n^{0} = 1 \qquad$

$n^{-m} = 1/(\underbrace{n\times\cdots\times n}_m) = \frac{1}{n^m} = (\frac{1}{n})^{m} \qquad (n \ne 0)$。

分數為指數的冪定義為$x^{\frac{m}{n}} = \sqrt[n]{x^{m}}$，即x的m次方开n次方根

0的0次方目前數學家沒有給予正式的定義，部分領域中，如組合數學，常用的慣例是定義為1。也有人主張定義為1。

冪不符合結合律和交換律。

因為十的次方很易計算，只需在後加零即可，所以科学记数法借助此簡化記錄數的方式；二的幂在計算機科學中很有用。

重要的恆等式

运算法则

$a^{m + n} = a^m \times a^n$

$a^{m - n} = \frac{a^m}{a^n}$

如果a ≠ 0，则$(a^m)^n = a^{m \cdot n}$

$(a \times b)^n = a^n \times b^n$

其他等式

• $a^\frac{m}{n} = \sqrt[n]{a^m}$
• $x^{-m} = \frac{1}{x^m} \qquad (x \ne 0)$
• $x^0 = 1 \qquad$
• $x^1 = x\,\!$
• $x^{-1} = \frac{1}{x} \qquad (x \ne 0)$
• $( x^m )^n = x^{mn}$
• $x^i = e^{i \ln x} = \cos(\ln x) + i \sin (\ln x), \quad i^2 = -1$

运算律

加法和乘法遵守交换律，比如：2+3 = 5 = 3+2，2×3 = 6 = 3×2，但是幂的运算不遵守交换律，$2^3 = 8$，但是$3^2 = 9$。

同样，加法和乘法遵守结合律，比如：(2+3)+4 = 9 = 2+(3+4)，(2×3)×4 = 24 = 2×(3×4)，幂同样不遵守：$(2^3)^4 = 8^4 = 4096$，但是$2^{(3^4)} = 2^{81} = 2,417,851,639,229,258,349,412,352$。

幂的运算顺序通常由上到下：

$a^{b^c} = a^{(b^c)}\ne (a^b)^c = a^{(b\times c)} = a^{b\times c}.$

整数指数幂

整数指数幂的运算只需要初等代数的知识。

正整数指数幂

表达式$a^2 = a\cdot a$被称作a的平方，因为边长为a的正方形面积是$a^2$。

表达式$a^3 = a\cdot a\cdot a$被称作a的立方，因为邊长为a的正方体体积是$a^3$。

所以$3^2$读作3的平方，$2^3$读作2的立方。

指数表示的是有多少个底数相乘。比如$3^5 = 3\times 3\times 3\times 3\times 3 = 243$，指数是5，底数是3，表示有5个3相乘。

或者，整数指数幂可以递归地定义成：

$a^n= \begin{cases} 1 & (n= 0) \\ a \cdot a^{n-1} & (n> 0) \\ \frac 1 a^{-n} & (n< 0) \end{cases}$

指数是1或者0

注意$3^1$表示仅仅1个3的乘积，就等于3。

注意$3^5 = 3\times 3^4$，$3^4 = 3\times 3^3$，$3^3 = 3\times 3^2$，$3^2=3\times 3^1$，

继续，得到$3^1 = 3\times 3^0 = 3$，所以$3^0 = 1$

另一个得到此结论的方法是：通过运算法则$\frac{x^n}{x^m} = x^{n - m}$

当$m=n$时，$1 = \frac{x^n}{x^n} = x^{n - n} = x^0$

• 任何数的1次方是它本身。

负数指数

我们定义任何不为0的数的-1次方等于它的倒数。

$a^{-1} = \frac{1}{a}.$

对于非零a定义$a^{-n} = \frac{1}{a^n}$。因为当$a=0$时分母是0而没有意义。

这个定义是因为$a^m\cdot a^n = a^{m+n}$，当m=-n时

$a^{-n} \, a^{n} = a^{-n\,+\,n} = a^0 = 1,$

因为$a^0$已经定义了，所以$a^{-n} = \frac{1}{a^{n}}$。

或者还可以像定义a的0次方一样定义：

通过运算法则$\frac{x^m}{x^n} = x^{m - n}$

当$m=0$时，可以约去分子得$x^{-n} = x^{0-n} = \frac{x^0}{x^n}$

负数指数$a^{-n}$还可以表示成1连续除以n个a。比如：

$3^{-4} = (((1/3)/3)/3)/3 = \frac{1}{81} = \frac{1}{3^{4}}$.

特殊数的幂

10的幂

在十进制的计数系统中，10的幂写成1后面跟着很多个0。例如：$10^3 = 1000,\ 10^{-3} = 0.001$

因此10的幂用来表示非常大或者非常小的数字。如：299,792,458 (真空中光速，单位是米每秒)，可以被写成$2.99792458\times 10^8$，近似值$2.998\times 10^8$.

国际单位制词头也使用10的幂来描述特别大或者特别小的数字，比如：词头“千”就是$10^3$，词头“毫”就是$10^{-3}$

1的幂

1的任何次幂都为1

0的幂

0的正数幂都等于0。

0的负数幂没有定义。

• 0的0次方是懸而未決的，某些領域下常用的慣例是約定為1。但某些教科書表示0的0次方為無意義。

负1的幂

-1的奇数幂等于-1

-1的偶数幂等于1

指数非常大时的幂

一个大于1的数的幂趋于无穷大，一个小于-1的数的幂趋于负无穷大

当$a > 1$，$n \to \infty$，$a^n \to \infty$

当$a < -1$，$n \to \infty$，$a^n \to -\infty$

一个绝对值小于1的数的幂趋于0

当$|a| < 1$，$n \to \infty$，$a^n \to 0$

1的幂永远都是1

当$a = 1$，$n \to \infty$，$a^n \to 1$

如果数a趋于1而它的幂趋于无穷，那么极限并不一定是上面几个。一个很重要的例子是：

当$n \to \infty, (1+\frac{1}{n})^n \to e$

参见e的幂

其他指数的极限参见幂的极限

正实数的实数幂

一个正实数的实数幂可以通过两种方法实现。

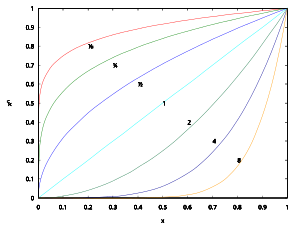
• 有理数幂可以通过N次方根定义，任何非0实数次幂都可以这样定义
• 自然对数可以被用来通过指数函数定义实数幂

N次方根

从上到下：$x^{\frac{1}{8}},\ x^{\frac{1}{4}},\ x^{\frac{1}{2}},\ x^{1},\ x^{2},\ x^{4},\ x^{8}$

一个数a的n次方根是x，x使$x^n=a$。

如果a是一个正实数，n是正整数，那么方程$x^n=a$只有一个正实数根。 这个根被称为a的n次方根，记作：$\sqrt[n]{a}$，其中$\sqrt{\ }$叫做根号。或者，a的n次方根也可以写成$a^{\frac{1}{n}}$. 例如$4^{\frac{1}{2}} = 2,\ 8^{\frac{1}{3}} = 2$

当指数是$\frac{1}{2}$时根号上的2可以省略，如：$\sqrt{4} = \sqrt[2]{4} = 2$

有理数幂

有理数指数通常可以理解成

$a^{\frac{m}{n}} = (a^m)^{\frac{1}{n}} = \sqrt[n]{a^m}$

e的幂

这个重要的数学常数e，有时被叫做欧拉数，近似2.718，是自然对数的底。它提供了定义非整数指数幂的一个方法。 它是从以下极限定义的：

$e =\lim_{n \to \infty} (1+\frac{1}{n} )^n$

指数函数的定义是：

$e^x =\lim_{n \to \infty} (1+\frac{x}{n} )^n$

可以很简单地证明e的正整数k次方$e^k$是：

$e^k = (\lim_{n \to \infty} (1+\frac{1}{n} ) ^n)^k$

$= \lim_{n \to \infty} ((1+\frac{1}{n} ) ^n)^k$

$= \lim_{n \to \infty} (1+\frac k {n\cdot k} )^{n \cdot k}$

$= \lim_{n \cdot k \to \infty} (1+\frac k {n\cdot k} )^{n \cdot k}$

$= \lim_{m \to \infty} (1+\frac k m )^m$

实数指数幂

因为所有实数可以近似地表示为有理数，任意实数指数x可以定义成：

$b^x = \lim_{r \to x} b^r,$

例如：

$x \approx 1.732$

于是

$5^x \approx 5^{1.732} =5^{433/250}=\sqrt[250]{5^{433}} \approx 16.241$

实数指数幂通常使用对数来定义，而不是近似有理数。

自然对数$\ln{x}$是指数函数$e^x$的反函数。 它的定义是：对于任意$b>0$，满足

$b = e^{\ln b}$

根据对数和指数运算的规则：

$b^x = (e^{\ln b})^x = e^{x \cdot\ln b}$

这就是实数指数幂的定义：

$b^x = e^{x\cdot\ln b}\,$

实数指数幂$b^x$的这个定义和上面使用有理数指数和连续性的定义相吻合。对于复数，这种定义更加常用。

负实数的实数幂

如果a是负数且n是偶数，那么$x^n = a$无实数解。 如果a是负数且n是奇数，那么$x^n = a$有一个负数解。

使用对数和有理数指数都不能将$a^k$（其中a是负实数，k实数）定义成实数。在一些特殊情况下，给出一个定义是可行的：负指数的整数指数幂是实数，有理数指数幂对于$a^\frac{m}{n}$（n是奇数）可以使用n次方根来计算，但是因为没有实数x使$x^2 = -1$，对于$a^\frac{m}{n}$（n是偶数）时必须使用虚数单位i。

使用对数的方法不能定义a ≤ 0时的$a^k$为实数。实际上，$e^x$对于任何实数x都是正的，所以$\ln(a)$对于负数没有意义。

使用有理数指数幂来逼近的方法也不能用于负数a因为它依赖于连续性。函数$f(r) = a^r$对于任何正的有理数a是连续的，但是对于负数a，函数f在有些有理数r上甚至不是连续的。

例如：当a = -1，它的奇数次根等于-1。所以如果n是正奇数整数，$-1^{\frac m n}=-1$当m是奇数，$-1^{\frac m n}=1$当m是偶数。虽然有理数q使$-1^q=1$的集合是稠密集，但是有理数q使$-1^q=-1$的集合也是。所以函数$-1^q$在有理数域不是连续的。

正实数的复数幂

e的虚数次幂

指数函数e^z可以通过(1 + z/N)^N当N趋于无穷大时的极限来定义，那么e^iπ就是(1 + iπ/N)^N的极限。在这个动画中n从1取到100。(1 + iπ/N)^N的值通过N重复增加在复数平面上展示，最终结果就是(1 + iπ/N)^N的准确值。可以看出，随着N的增大，(1 + iπ/N)^N逐渐逼近极限-1。这就是欧拉公式。

复数运算的几何意义和e的幂可以帮助我们理解$e^{ix}$（x是实数）。想象一个直角三角形(0, 1, 1 + ix/n)（括号内是复数平面内三角形的三个顶点），对于足够大的n，这个三角形可以看作一个扇形，这个扇形的中心角就等于x/n弧度。对于所有k，三角形(0, (1 + ix/n)^k, (1 + ix/n)^k+1)互为相似三角形。所以当n足够大时(1 + ix/n)ⁿ的极限是复数平面上的单位圆上x弧度的点。这个点的极坐标是(r, θ) = (1, x),，直角坐标是（cos x, sin x）。所以$e^{ix} = \cos x + i \sin x$。这就是欧拉公式，它通过复数的意义将代数学和三角学联系起来了。

等式$e^z = 1$的解是一个整数乘以2iπ：

$\{ z : e^z = 1 \} = \{ 2k\pi i : k \in \mathbb{Z} \}.$

更一般地，如果$e^b = a$，那么$e^z = a$的每一个解都可以通过将2iπ的整数倍加上b得到：

$\{ z : e^z = a \} = \{ b + 2k\pi i : k \in \mathbb{Z} \}.$

这个复指数函数是一个有周期2iπ的周期函数。

更简单的：$e^{i\pi} = -1;\ e^{x + iy}= e^x(\cos y + i \sin y )$。

三角函数

根据欧拉公式，三角函数余弦和正弦是：

$\cos z = \frac{ e^{i\cdot z} + e^{-i\cdot z}} {2} \qquad \sin z = \frac{e^{i\cdot z} - e^{-i\cdot z}}{2\cdot i}$

历史上，在复数发明之前，余弦和正弦是用几何的方法定义的。上面的公式将复杂的三角函数的求和公式转换成了简单的指数方程

$e^{i\cdot (x+y)}=e^{i\cdot x}\cdot e^{i\cdot y}.\,$

使用了复数指数幂之后，很多三角学问题都能够使用代数方法解决。

e的复数指数幂

$e^{x+iy}$可以分解成$e^x\cdot e^{iy}$。其中$e^x$是$e^{x+iy}$的模，$e^{iy}$决定了$e^{x+iy}$的方向

正实数的复数幂

如果a是一个正实数，z是任何复数，$a^z$定义成$e^{z\cdot \ln(a)}$，其中x = ln(a)是方程$e^x = a$的唯一解。所以处理实数的方法同样可以用来处理复数。

例如：

$2^i = e^{i\cdot \ln(2)} = \cos{\ln 2}+i\cdot \sin{\ln 2 } = 0.7692+0.63896i$

$e^i = 0.54030+0.84147i$

$10^i = -0.66820+0.74398i$

$(e^{2\pi})^i = 535.49^i = 1$

在函數中

當函數名後有上標的數（即函數的指數），一般指要重複它的運算。例如$f^3 (x )$即$f \left\{ f \left[ f ( x ) \right] \right\}$。特別地，$f^{-1} (x )$指$f (x )$的反函數。

但三角函数的情況有所不同，一個正指數應用於函數的名字時，指答案要進行乘方運算，而指數為-1時则表示其反函數。例如：$(\sin x)^{-1}$表示$\csc x$。因此在三角函數時，使用$\sin^{-1} x$來表示$\sin x$的反函數$\arcsin x$。

另見

• 迭代冪次

外部鏈結

• 指數的歷史

乘方的结果叫做幂（power）通常我们把多项式的各项排序的时候分为降幂与升幂，升幂是一个多项式排序为从小到大，降幂而是一个多项式排序为从大到小..