此条目页的主題是代数概念。关于几何定理,請見「
圆幂定理 」。
b n 记号
底数
b
{\displaystyle b}
n
{\displaystyle n}
在数学 中,重复连乘的运算叫做乘方 ,乘方的结果称为 幂 [1] mathematical power ,power);由此,若
n
{\displaystyle n}
正整數 ,
n
{\displaystyle n}
b
{\displaystyle b}
b
{\displaystyle b}
n
{\displaystyle n}
b
n
{\displaystyle b^{n}}
b
n
=
b
×
⋯
×
b
⏟
n
{\displaystyle b^{n}=\underbrace {b\times \cdots \times b} _{n}}
幂運算 (exponentiation )又稱指數運算 、取冪 [2] 數學 運算 ,表達式 為
b
n
{\displaystyle b^{n}}
b
{\displaystyle b}
n
{\displaystyle n}
b
{\displaystyle b}
n
{\displaystyle n}
b
{\displaystyle b}
底數 ,而
n
{\displaystyle n}
指數 ,通常指數寫成上標 ,放在底數的右邊 。在純文字格式等不能用上標的情況,例如在編程語言 或電子郵件 中,
b
n
{\displaystyle b^{n}}
b^n 或 b**n ;也可視為超運算 ,記為 b[3]n ;亦可以用高德納箭號表示法 ,寫成 b↑n 。
當指數為 1 時,通常不寫出來,因為運算出的值和底數的數值 一樣;指數為 2 時,可以讀作“
b
{\displaystyle b}
平方 ”;指數為 3 時,可以讀作“
b
{\displaystyle b}
立方 ”。
由於在十进制 中,十的冪 很容易計算,只需在後面加零即可,所以科学记数法 借此簡化 記錄 的數字;二的幂 則在計算機科學 中相當重要。
起始值 1(乘法的單位元 )乘上底數(
b
{\displaystyle b}
n
{\displaystyle n}
[需要解释 。這樣定義 了後,很易想到如何一般化指數 0 和負數的情況:指數是零時,底數不為零,冪均為一(即除 0 外,所有數的 0 次方都是 1 );指數是負數時,就等於重複除以 底數(或底數的倒數 自乘指數這麼多次),即:
b
0
=
1
(
b
≠
0
)
{\displaystyle b^{0}=1\qquad (b\neq 0)}
b
−
n
=
1
b
×
⋯
×
b
⏟
n
=
1
b
n
=
(
1
b
)
n
(
b
≠
0
)
{\displaystyle b^{-n}={1 \over \underbrace {b\times \cdots \times b} _{n}}={\frac {1}{b^{n}}}=\left({\frac {1}{b}}\right)^{n}\qquad (b\neq 0)}
若以分數 為指數的冪,則定義:
b
n
m
=
b
n
m
{\displaystyle b^{\frac {n}{m}}={\sqrt[{m}]{b^{n}}}}
即
b
{\displaystyle b}
n
{\displaystyle n}
m
{\displaystyle m}
方根 。
0的0次方 (
0
0
{\displaystyle 0^{0}}
數學家 給予正式的定義;在部分數學領域 中,如組合數學 ,常用的慣例是定義為 1 。
此外,當
n
{\displaystyle n}
複數 ,且
b
{\displaystyle b}
實數 時,
b
n
=
exp
(
n
ln
(
b
)
)
{\displaystyle b^{n}=\exp(n\ln(b))}
exp 是指數函數 ,而 ln 是自然對數 。
运算法则 [ 编辑 ]
a
m
×
a
n
=
a
m
+
n
{\displaystyle a^{m}\times a^{n}=a^{m+n}}
a
m
÷
a
n
=
a
m
−
n
{\displaystyle a^{m}\div a^{n}=a^{m-n}}
同指数幂相除,指数不变,底数相除(
b
{\displaystyle b}
a
n
b
n
=
(
a
b
)
n
{\displaystyle {\frac {a^{n}}{b^{n}}}=\left({\frac {a}{b}}\right)^{n}}
其他等式 [ 编辑 ]
x
m
n
=
x
m
n
{\displaystyle x^{\frac {m}{n}}={\sqrt[{n}]{x^{m}}}}
x
−
m
=
1
x
m
(
x
≠
0
)
{\displaystyle x^{-m}={\frac {1}{x^{m}}}\qquad (x\neq 0)}
x
0
=
1
(
x
≠
0
)
{\displaystyle x^{0}=1\qquad (x\neq 0)}
x
1
=
x
{\displaystyle x^{1}=x\,\!}
x
−
1
=
1
x
(
x
≠
0
)
{\displaystyle x^{-1}={\frac {1}{x}}\qquad (x\neq 0)}
运算律 [ 编辑 ] 加法和乘法存在交换律 ,比如:
2
+
3
=
5
=
3
+
2
{\displaystyle 2+3=5=3+2}
2
×
3
=
6
=
3
×
2
{\displaystyle 2\times 3=6=3\times 2}
2
3
=
8
{\displaystyle 2^{3}=8}
3
2
=
9
{\displaystyle 3^{2}=9}
同样,加法和乘法存在结合律 ,比如:
(
2
+
3
)
+
4
=
9
=
2
+
(
3
+
4
)
{\displaystyle (2+3)+4=9=2+(3+4)}
(
2
×
3
)
×
4
=
24
=
2
×
(
3
×
4
)
{\displaystyle (2\times 3)\times 4=24=2\times (3\times 4)}
(
2
3
)
4
=
8
4
=
4096
{\displaystyle (2^{3})^{4}=8^{4}=4096}
2
(
3
4
)
=
2
81
=
2
,
417
,
851
,
639
,
229
,
258
,
349
,
412
,
352
{\displaystyle 2^{(3^{4})}=2^{81}=2,417,851,639,229,258,349,412,352}
(
2
3
)
4
≠
2
(
3
4
)
{\displaystyle (2^{3})^{4}\neq 2^{(3^{4})}}
但是冪運算仍然有其運算律,稱為指數律 :
a
m
⋅
a
n
=
a
m
+
n
{\displaystyle a^{m}\cdot a^{n}=a^{m+n}}
a
m
a
n
=
a
m
−
n
{\displaystyle {\frac {a^{m}}{a^{n}}}=a^{m-n}}
(
a
m
)
n
=
a
m
n
{\displaystyle (a^{m})^{n}=a^{mn}}
a
m
n
=
a
m
n
{\displaystyle {\sqrt[{n}]{a^{m}}}=a^{\frac {m}{n}}}
a
n
⋅
b
n
=
(
a
⋅
b
)
n
{\displaystyle a^{n}\cdot b^{n}=(a\cdot b)^{n}}
a
n
b
n
=
(
a
b
)
n
{\displaystyle {\frac {a^{n}}{b^{n}}}=\left({\frac {a}{b}}\right)^{n}}
整数指数幂 [ 编辑 ] 整数指数幂的运算只需要初等代数 的知识。
正整数指数幂 [ 编辑 ] 表达式
a
2
=
a
⋅
a
{\displaystyle a^{2}=a\cdot a}
a
{\displaystyle a}
平方 ,因为边长为
a
{\displaystyle a}
a
2
{\displaystyle a^{2}}
表达式
a
3
=
a
⋅
a
⋅
a
{\displaystyle a^{3}=a\cdot a\cdot a}
a
{\displaystyle a}
立方 ,因为邊长为
a
{\displaystyle a}
a
3
{\displaystyle a^{3}}
所以
3
2
{\displaystyle 3^{2}}
2
3
{\displaystyle 2^{3}}
指数表示的是底数反复相乘多少次。比如
3
5
=
3
×
3
×
3
×
3
×
3
=
243
{\displaystyle 3^{5}=3\times 3\times 3\times 3\times 3=243}
或者,整数指数幂可以递归 地定义成:
a
n
=
{
1
(
n
=
0
)
a
⋅
a
n
−
1
(
n
>
0
)
(
1
a
)
−
n
(
n
<
0
)
{\displaystyle a^{n}={\begin{cases}1&(n=0)\\a\cdot a^{n-1}&(n>0)\\\left({\frac {1}{a}}\right)^{-n}&(n<0)\end{cases}}}
指数是1或者0 [ 编辑 ] 注意
3
1
{\displaystyle 3^{1}}
注意
3
5
=
3
×
3
4
{\displaystyle 3^{5}=3\times 3^{4}}
3
4
=
3
×
3
3
{\displaystyle 3^{4}=3\times 3^{3}}
3
3
=
3
×
3
2
{\displaystyle 3^{3}=3\times 3^{2}}
3
2
=
3
×
3
1
{\displaystyle 3^{2}=3\times 3^{1}}
继续,得到
3
1
=
3
×
3
0
=
3
{\displaystyle 3^{1}=3\times 3^{0}=3}
3
0
=
1
{\displaystyle 3^{0}=1}
另一个得到此结论的方法是:通过运算法则
x
n
x
m
=
x
n
−
m
{\displaystyle {\frac {x^{n}}{x^{m}}}=x^{n-m}}
当
m
=
n
{\displaystyle m=n}
1
=
x
n
x
n
=
x
n
−
n
=
x
0
{\displaystyle 1={\frac {x^{n}}{x^{n}}}=x^{n-n}=x^{0}}
零的零次方 [ 编辑 ]
0
0
{\displaystyle 0^{0}}
0
0
=
1
{\displaystyle 0^{0}=1}
0
∗
∗
0
=
1
{\displaystyle 0**0=1}
在这里给出这一种极限的看法
lim
x
→
0
+
x
x
=
0
0
{\displaystyle \lim _{x\to 0^{+}}x^{x}=0^{0}}
负数指数 [ 编辑 ] 我们定义任何不为 0 的数 a 的 -1 次方等于它的倒数。
a
−
1
=
1
a
{\displaystyle a^{-1}={\frac {1}{a}}}
对于非零
a
{\displaystyle a}
a
−
n
=
1
a
n
{\displaystyle a^{-n}={\frac {1}{a^{n}}}}
而
a
=
0
{\displaystyle a=0}
0 没有意义。
证法一:
根据定义
a
m
⋅
a
n
=
a
m
+
n
{\displaystyle a^{m}\cdot a^{n}=a^{m+n}}
m
=
−
n
{\displaystyle m=-n}
a
−
n
a
n
=
a
−
n
+
n
=
a
0
=
1
,
{\displaystyle a^{-n}\,a^{n}=a^{-n\,+\,n}=a^{0}=1,}
得
a
−
n
a
n
=
1
{\displaystyle a^{-n}\,a^{n}=1}
a
−
n
=
1
a
n
{\displaystyle a^{-n}={\frac {1}{a^{n}}}}
证法二:
通过运算法则
a
m
a
n
=
a
m
−
n
{\displaystyle {\frac {a^{m}}{a^{n}}}=a^{m-n}}
当
m
=
0
{\displaystyle m=0}
a
−
n
=
a
0
−
n
=
a
0
a
n
=
1
a
n
{\displaystyle a^{-n}=a^{0-n}={\frac {a^{0}}{a^{n}}}={\frac {1}{a^{n}}}}
负数指数
a
−
n
{\displaystyle a^{-n}}
1 连续除以
n
{\displaystyle n}
a
{\displaystyle a}
3
−
4
=
1
3
3
3
3
=
1
81
=
1
3
4
{\displaystyle 3^{-4}={\frac {\frac {\frac {\frac {1}{3}}{3}}{3}}{3}}={\frac {1}{81}}={\frac {1}{3^{4}}}}
特殊数的幂 [ 编辑 ] 10的幂 [ 编辑 ] 在十进制 的计数系统中,10的幂写成1后面跟着很多个0。例如:
10
3
=
1000
,
10
−
3
=
0.001
{\displaystyle 10^{3}=1000,\ 10^{-3}=0.001}
因此10的幂用来表示非常大或者非常小的数字。如:299,792,458(真空中光速 ,单位是米每秒 ),可以写成
2.99792458
×
10
8
{\displaystyle 2.99792458\times 10^{8}}
近似值
2.998
×
10
8
{\displaystyle 2.998\times 10^{8}}
3
×
10
8
{\displaystyle 3\times 10^{8}}
国际单位制词头 也使用10的幂来描述特别大或者特别小的数字,比如:词头“千”就是
10
3
{\displaystyle 10^{3}}
10
−
3
{\displaystyle 10^{-3}}
2的幂 [ 编辑 ] 1的幂 [ 编辑 ] 1的任何次幂都为1。
0的幂 [ 编辑 ] 0的正数幂都等于0。
0的负数幂没有定义。
任何非0之数的0次方都是1;而0的0次方 是懸而未決的,某些領域下常用的慣例是約定為1。[3] [4]
负1的幂 [ 编辑 ] -1的奇数幂等于-1
-1的偶数幂等于1
指数非常大时的幂 [ 编辑 ] 一个大于1的数的幂趋于无穷大 ,一个小于-1的数的幂趋于负无穷大
当
a
>
1
{\displaystyle a>1}
n
→
∞
{\displaystyle n\to \infty }
a
n
→
∞
{\displaystyle a^{n}\to \infty }
当
a
<
−
1
{\displaystyle a<-1}
n
→
∞
{\displaystyle n\to \infty }
a
n
→
−
∞
{\displaystyle a^{n}\to -\infty }
∞
{\displaystyle \infty }
一个绝对值小于1的数的幂趋于0
当
|
a
|
<
1
{\displaystyle |a|<1}
n
→
∞
{\displaystyle n\to \infty }
a
n
→
0
{\displaystyle a^{n}\to 0}
1的幂永远都是1
当
a
=
1
{\displaystyle a=1}
n
→
∞
{\displaystyle n\to \infty }
a
n
→
1
{\displaystyle a^{n}\to 1}
如果数a 趋于1而它的幂趋于无穷,那么极限并不一定是上面几个。一个很重要的例子是:
当
n
→
∞
,
(
1
+
1
n
)
n
→
e
{\displaystyle n\to \infty ,\left(1+{\frac {1}{n}}\right)^{n}\to e}
参见e的幂
其他指数的极限参见幂的极限
正实数的实数幂 [ 编辑 ] 一个正实数的实数 幂可以通过两种方法实现。
有理数 幂可以通过N次方根 定义,任何非0实数次幂都可以这样定义自然对数 可以被用来通过指数函数定义实数幂N次方根 [ 编辑 ] 从上到下:
x
1
8
,
x
1
4
,
x
1
2
,
x
1
,
x
2
,
x
4
,
x
8
{\displaystyle x^{\frac {1}{8}},\ x^{\frac {1}{4}},\ x^{\frac {1}{2}},\ x^{1},\ x^{2},\ x^{4},\ x^{8}}
一个数
a
{\displaystyle a}
n
{\displaystyle n}
x
{\displaystyle x}
x
{\displaystyle x}
x
n
=
a
{\displaystyle x^{n}=a}
如果
a
{\displaystyle a}
n
{\displaystyle n}
x
n
=
a
{\displaystyle x^{n}=a}
根 。
这个根被称为
a
{\displaystyle a}
n
{\displaystyle n}
a
n
{\displaystyle {\sqrt[{n}]{a}}}
{\displaystyle {\sqrt {\ }}}
a
{\displaystyle a}
n
{\displaystyle n}
a
1
n
{\displaystyle a^{\frac {1}{n}}}
4
1
2
=
2
,
8
1
3
=
2
{\displaystyle 4^{\frac {1}{2}}=2,\ 8^{\frac {1}{3}}=2}
当指数是
1
2
{\displaystyle {\frac {1}{2}}}
4
=
4
1
2
=
4
2
=
2
{\displaystyle {\sqrt {4}}=4^{\frac {1}{2}}={\sqrt[{2}]{4}}=2}
有理数幂 [ 编辑 ] 有理数指数幂定义为
a
m
n
=
(
a
m
)
1
n
=
a
m
n
{\displaystyle a^{\frac {m}{n}}=(a^{m})^{\frac {1}{n}}={\sqrt[{n}]{a^{m}}}}
e的幂 [ 编辑 ] 这个重要的数学常数e 欧拉数 ,近似2.718,是自然对数 的底。它提供了定义非整数指数幂的一个方法。
它是从以下极限定义的:
e
=
lim
n
→
∞
(
1
+
1
n
)
n
{\displaystyle e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}
指数函数
e
x
=
lim
n
→
∞
(
1
+
x
n
)
n
{\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}
可以很简单地证明e 的正整数k 次方
e
k
{\displaystyle e^{k}}
e
k
=
[
lim
n
→
∞
(
1
+
1
n
)
n
]
k
{\displaystyle e^{k}=\left[\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right]^{k}}
=
lim
n
→
∞
[
(
1
+
1
n
)
n
]
k
{\displaystyle =\lim _{n\to \infty }\left[\left(1+{\frac {1}{n}}\right)^{n}\right]^{k}}
=
lim
n
→
∞
(
1
+
k
n
⋅
k
)
n
⋅
k
{\displaystyle =\lim _{n\to \infty }\left(1+{\frac {k}{n\cdot k}}\right)^{n\cdot k}}
=
lim
n
⋅
k
→
∞
(
1
+
k
n
⋅
k
)
n
⋅
k
{\displaystyle =\lim _{n\cdot k\to \infty }\left(1+{\frac {k}{n\cdot k}}\right)^{n\cdot k}}
=
lim
m
→
∞
(
1
+
k
m
)
m
{\displaystyle =\lim _{m\to \infty }\left(1+{\frac {k}{m}}\right)^{m}}
实数指数幂 [ 编辑 ] y = bx 對各種底數b的圖像,分別為綠色的10、紅色的e、藍色的2和青色的1/2。因为所有实数 可以近似地表示为有理数,任意实数指数x 可以定义成[5]
b
x
=
lim
r
→
x
b
r
,
{\displaystyle b^{x}=\lim _{r\to x}b^{r},}
例如:
x
≈
1.732
{\displaystyle x\approx 1.732}
于是
5
x
≈
5
1.732
=
5
433
250
=
5
433
250
≈
16.241
{\displaystyle 5^{x}\approx 5^{1.732}=5^{\frac {433}{250}}={\sqrt[{250}]{5^{433}}}\approx 16.241}
实数指数幂通常使用对数来定义,而不是近似有理数。
自然对数
ln
x
{\displaystyle \ln {x}}
e
x
{\displaystyle e^{x}}
反函数 。
它的定义是:对于任意
b
>
0
{\displaystyle b>0}
b
=
e
ln
b
{\displaystyle b=e^{\ln b}}
根据对数和指数运算的规则:
b
x
=
(
e
ln
b
)
x
=
e
x
⋅
ln
b
{\displaystyle b^{x}=(e^{\ln b})^{x}=e^{x\cdot \ln b}}
这就是实数指数幂的定义:
b
x
=
e
x
⋅
ln
b
{\displaystyle b^{x}=e^{x\cdot \ln b}\,}
实数指数幂
b
x
{\displaystyle b^{x}}
负实数的实数幂 [ 编辑 ] 如果
a
{\displaystyle a}
n
{\displaystyle n}
偶数 ,那么
x
=
a
n
{\displaystyle x=a^{n}}
a
{\displaystyle a}
n
{\displaystyle n}
奇数 ,那么
x
=
a
n
{\displaystyle x=a^{n}}
使用对数和有理数指数都不能将
a
k
{\displaystyle a^{k}}
a
{\displaystyle a}
k
{\displaystyle k}
a
m
n
{\displaystyle a^{\frac {m}{n}}}
n
{\displaystyle n}
n
{\displaystyle n}
x
{\displaystyle x}
x
2
=
−
1
{\displaystyle x^{2}=-1}
a
m
n
{\displaystyle a^{\frac {m}{n}}}
n
{\displaystyle n}
虚数单位
i
{\displaystyle i}
使用对数的方法不能定义
a
≤
0
{\displaystyle a\leq 0}
a
k
{\displaystyle a^{k}}
e
x
{\displaystyle e^{x}}
x
{\displaystyle x}
ln
(
a
)
{\displaystyle \ln(a)}
使用有理数指数幂来逼近的方法也不能用于负数
a
{\displaystyle a}
连续性 。函数
f
(
r
)
=
a
r
{\displaystyle f(r)=a^{r}}
a
{\displaystyle a}
a
{\displaystyle a}
f
{\displaystyle f}
r
{\displaystyle r}
例如:当
a
=
−
1
{\displaystyle a=-1}
n
{\displaystyle n}
−
1
m
n
=
−
1
{\displaystyle -1^{\frac {m}{n}}=-1}
m
{\displaystyle m}
−
1
m
n
=
1
{\displaystyle -1^{\frac {m}{n}}=1}
m
{\displaystyle m}
q
{\displaystyle q}
−
1
q
=
1
{\displaystyle -1^{q}=1}
集合 是稠密集 ,但是有理数
q
{\displaystyle q}
−
1
q
=
−
1
{\displaystyle -1^{q}=-1}
集合 也是。所以函数
−
1
q
{\displaystyle -1^{q}}
因此,如果要求负实数的任意实数幂,必须将底数和指数看成複數 ,按复数的正实数幂或复数的复数幂方法计算。
正实数的复数幂 [ 编辑 ] e的虚数次幂 [ 编辑 ] 指数函数 e z (1 + z /N )N 当N 趋于无穷大时的极限 来定义,那么e iπ (1 + iπ /N )N 的极限。在这个动画中n 从1取到100。(1 + iπ /N )N 的值通过N 重复增加在复数平面上展示,最终结果就是(1 + iπ /N )N 的准确值。可以看出,随着N 的增大,(1 + iπ /N )N 逐渐逼近极限-1。这就是欧拉公式 。複數 运算的几何意义和e 的幂
e
i
x
{\displaystyle e^{ix}}
x
{\displaystyle x}
純虛數指數函數 。想象一个直角三角形
(
0
,
1
,
1
+
i
x
n
)
{\displaystyle (0,1,1+{\frac {ix}{n}})}
顶点 ),对于足够大的
n
{\displaystyle n}
扇形 ,这个扇形的中心角就等于
x
n
{\displaystyle {\frac {x}{n}}}
弧度 。对于所有
k
{\displaystyle k}
(
0
,
(
1
+
i
x
n
)
k
,
(
1
+
i
x
n
)
k
+
1
)
{\displaystyle (0,(1+{\frac {ix}{n}})^{k},(1+{\frac {ix}{n}})^{k+1})}
相似三角形 。所以当
n
{\displaystyle n}
(
1
+
i
x
n
)
n
{\displaystyle (1+{\frac {ix}{n}})^{n}}
单位圆 上
x
{\displaystyle x}
极坐标 是
(
r
,
θ
)
=
(
1
,
x
)
{\displaystyle (r,\theta )=(1,x)}
直角坐标 是
(
cos
x
,
sin
x
)
{\displaystyle (\cos x,\sin x)}
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
純虛數指數函數 。这就是欧拉公式 ,它通过複數 的意义将代数学 和三角学 联系起来了。
等式
e
z
=
1
{\displaystyle e^{z}=1}
2
i
π
{\displaystyle 2i\pi }
[6]
{
z
:
e
z
=
1
}
=
{
2
k
π
i
:
k
∈
Z
}
.
{\displaystyle \{z:e^{z}=1\}=\{2k\pi i:k\in \mathbb {Z} \}.}
更一般地,如果
e
b
=
a
{\displaystyle e^{b}=a}
e
z
=
a
{\displaystyle e^{z}=a}
2
i
π
{\displaystyle 2i\pi }
b
{\displaystyle b}
{
z
:
e
z
=
a
}
=
{
b
+
2
k
π
i
:
k
∈
Z
}
.
{\displaystyle \{z:e^{z}=a\}=\{b+2k\pi i:k\in \mathbb {Z} \}.}
这个复指数函数是一个有周期
2
i
π
{\displaystyle 2i\pi }
周期函数 。
更简单的:
e
i
π
=
−
1
;
e
x
+
i
y
=
e
x
(
cos
y
+
i
sin
y
)
{\displaystyle e^{i\pi }=-1;\ e^{x+iy}=e^{x}(\cos y+i\sin y)}
三角函数 [ 编辑 ] 根据欧拉公式 ,三角函数 余弦和正弦是:
cos
z
=
e
i
⋅
z
+
e
−
i
⋅
z
2
sin
z
=
e
i
⋅
z
−
e
−
i
⋅
z
2
⋅
i
{\displaystyle \cos z={\frac {e^{i\cdot z}+e^{-i\cdot z}}{2}}\qquad \sin z={\frac {e^{i\cdot z}-e^{-i\cdot z}}{2\cdot i}}}
历史上,在复数发明之前,余弦和正弦是用几何的方法定义的。上面的公式将复杂的三角函数的求和公式转换成了简单的指数方程
e
i
⋅
(
x
+
y
)
=
e
i
⋅
x
⋅
e
i
⋅
y
.
{\displaystyle e^{i\cdot (x+y)}=e^{i\cdot x}\cdot e^{i\cdot y}.\,}
使用了复数指数幂之后,很多三角学问题都能够使用代数方法解决。
e的复数指数幂 [ 编辑 ]
e
x
+
i
y
{\displaystyle e^{x+iy}}
e
x
⋅
e
i
y
{\displaystyle e^{x}\cdot e^{iy}}
e
x
{\displaystyle e^{x}}
e
x
+
i
y
{\displaystyle e^{x+iy}}
模 ,
e
i
y
{\displaystyle e^{iy}}
e
x
+
i
y
{\displaystyle e^{x+iy}}
正实数的复数幂 [ 编辑 ] 如果
a
{\displaystyle a}
z
{\displaystyle z}
a
z
{\displaystyle a^{z}}
e
z
⋅
ln
(
a
)
{\displaystyle e^{z\cdot \ln(a)}}
x
=
ln
(
a
)
{\displaystyle x=\ln(a)}
e
x
=
a
{\displaystyle e^{x}=a}
例如:
2
i
=
e
i
⋅
ln
(
2
)
=
cos
ln
2
+
i
⋅
sin
ln
2
=
0.7692
+
0.63896
i
{\displaystyle 2^{i}=e^{i\cdot \ln(2)}=\cos {\ln 2}+i\cdot \sin {\ln 2}=0.7692+0.63896i}
e
i
=
0.5403023
+
0.841471
i
{\displaystyle {{e}^{i}}=0.5403023+0.841471i}
10
i
=
−
0.6682015
+
0.7439803
i
{\displaystyle {{10}^{i}}=-0.6682015+0.7439803i}
(
e
2
π
)
i
=
535.49
i
=
1
{\displaystyle (e^{2\pi })^{i}=535.49^{i}=1}
复数的复数幂 [ 编辑 ] 複數的虚数幂 [ 编辑 ] 让我们从一个简单的例子开始:计算
(
1
+
i
)
i
{\displaystyle \left(1+i\right)^{i}}
(
1
+
i
)
i
=
[
2
(
2
2
+
2
2
i
)
]
i
=
(
2
e
π
4
i
)
i
=
e
−
π
4
2
i
=
e
−
π
4
cos
ln
2
2
+
i
e
−
π
4
sin
ln
2
2
{\displaystyle {\begin{aligned}\left(1+i\right)^{i}&=\left[{\sqrt {2}}\left({\frac {\sqrt {2}}{2}}+{\frac {\sqrt {2}}{2}}i\right)\right]^{i}\\&=\left({\sqrt {2}}e^{{\tfrac {\pi }{4}}i}\right)^{i}\\&=e^{-{\tfrac {\pi }{4}}}{\sqrt {2}}^{i}\\&=e^{-{\tfrac {\pi }{4}}}\cos {\frac {\ln 2}{2}}+ie^{-{\tfrac {\pi }{4}}}\sin {\frac {\ln 2}{2}}\\\end{aligned}}}
其中
2
i
{\displaystyle {\sqrt {2}}^{i}}
正实数的复数幂
复数的复数幂 [ 编辑 ] 类似地,在计算复数的复数幂时,我们可以将指数的实部与虚部分开以进行幂计算。例如计算
(
1
+
i
)
2
+
i
{\displaystyle \left(1+i\right)^{2+i}}
(
1
+
i
)
2
+
i
=
(
1
+
i
)
2
(
1
+
i
)
i
=
2
i
e
−
π
4
(
cos
ln
2
2
+
i
sin
ln
2
2
)
=
−
2
e
−
π
4
sin
ln
2
2
+
2
i
e
−
π
4
cos
ln
2
2
{\displaystyle {\begin{aligned}\left(1+i\right)^{2+i}&=\left(1+i\right)^{2}\left(1+i\right)^{i}\\&=2ie^{-{\tfrac {\pi }{4}}}\left(\cos {\frac {\ln 2}{2}}+i\sin {\frac {\ln 2}{2}}\right)\\&=-2e^{-{\tfrac {\pi }{4}}}\sin {\frac {\ln 2}{2}}+2ie^{-{\tfrac {\pi }{4}}}\cos {\frac {\ln 2}{2}}\\\end{aligned}}}
一般情况 [ 编辑 ] 复数的复数幂必须首先化为底数为
e
{\displaystyle e}
w
z
=
e
z
ln
w
{\displaystyle w^{z}=e^{z\ln w}}
又,由复数的极坐标表示法:
w
=
r
e
i
θ
{\displaystyle w=re^{i\theta }}
故
w
z
=
e
z
ln
(
w
)
=
e
z
(
ln
(
r
)
+
i
θ
)
{\displaystyle w^{z}=e^{z\ln(w)}=e^{z(\ln(r)+i\theta )}}
然后,使用欧拉公式 处理即可。
由于复数的极坐标表示法中,辐角
θ
{\displaystyle \theta }
多值函数 。不过实际应用中,为了简便起见,辐角都只取主值,从而使幂值唯一。
當函數名後有上標的數(即函數的指數),一般指要重複它的運算。例如
f
3
(
x
)
{\displaystyle f^{3}(x)}
f
(
f
(
f
(
x
)
)
)
{\displaystyle f(f(f(x)))}
f
−
1
(
x
)
{\displaystyle f^{-1}(x)}
f
(
x
)
{\displaystyle f(x)}
反函數 。
但三角函数 的情況有所不同,一個正指數應用於函數的名字時,指答案要進行乘方運算,而指數為-1時则表示其反函數。例如:
(
sin
x
)
−
1
{\displaystyle (\sin x)^{-1}}
csc
x
{\displaystyle \csc x}
sin
−
1
x
{\displaystyle \sin ^{-1}x}
sin
x
{\displaystyle \sin x}
arcsin
x
{\displaystyle \arcsin x}
计算自然数(正整数)
n
{\displaystyle n}
a
n
{\displaystyle a^{n}}
[ 编辑 ] 最快的方式计算
a
n
{\displaystyle a^{n}}
n
{\displaystyle n}
除以2 的事实。
在C /C++语言 中,你可以写如下算法:
double power ( double a , unsigned int n )
{
double y = 1 ;
double f = a ;
while ( n > 0 ) {
if ( n % 2 == 1 ) y *= f ;
n >>= 1 ;
f *= f ;
}
return y ;
}
此算法的時間複雜度 為
O
(
log
n
)
{\displaystyle \mathrm {O} (\log n)\!}
時間複雜度 為
O
(
n
)
{\displaystyle \mathrm {O} (n)\!}
n
{\displaystyle n}
例如計算
a
100
{\displaystyle a^{100}}
a
n
(
n
<
0
)
{\displaystyle a^{n}(n<0)}
a
|
n
|
{\displaystyle a^{|n|}}
^ 李迪. 中国数学通史: 宋元卷. 江苏敎育出版社. 1999: 294. ISBN 9787534336928自乘为幂 ^ 存档副本 . [2022-10-21 ] . (原始内容存档 于2022-10-22). ^ Augustin-Louis Cauchy, Cours d'Analyse de l'École Royale Polytechnique (1821). In his Oeuvres Complètes , series 2, volume 3.
^ 康軒國中1上《FUN學練功坊①》P.35:a的0次方=1(a≠0)(註:0的0次方為無意義)
^ Denlinger, Charles G. Elements of Real Analysis . Jones and Bartlett. 2011: 278 –283. ISBN 978-0-7637-7947-4 ^ This definition of a principal root of unity can be found in:
外部連結 [ 编辑 ] 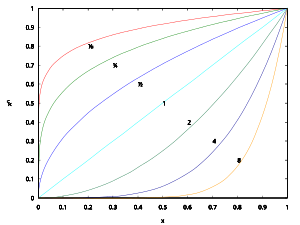

















![{\displaystyle \scriptstyle {\sqrt[{\text{根 指 数 }}]{\scriptstyle {\text{被 开 方 数 }}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/129356d757065c14aa96f75e3c93198f2e4fba94)







![{\displaystyle b^{\frac {n}{m}}={\sqrt[{m}]{b^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec978c5d8ef197c7c927037b592d372f3347031d)






![{\displaystyle x^{\frac {m}{n}}={\sqrt[{n}]{x^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c52238caa2a931ae81e11a0d2628e4f8e751aa32)
















![{\displaystyle {\sqrt[{n}]{a^{m}}}=a^{\frac {m}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c714f8be840b1ed81134c7179d0a72b3c0a76c9)





















































![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)




![{\displaystyle {\sqrt {4}}=4^{\frac {1}{2}}={\sqrt[{2}]{4}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90efca0389d4fc157651b7d95aacf2c8320b9ddd)
![{\displaystyle a^{\frac {m}{n}}=(a^{m})^{\frac {1}{n}}={\sqrt[{n}]{a^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba2eba0b756d798cc6556c5c75d38fd539080075)



![{\displaystyle e^{k}=\left[\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right]^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d3b8cad42a2358cb6e49e311eb7042342c2cfef)
![{\displaystyle =\lim _{n\to \infty }\left[\left(1+{\frac {1}{n}}\right)^{n}\right]^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/529771752e3387f5508779dd24b4e2bafc4a5efb)





![{\displaystyle 5^{x}\approx 5^{1.732}=5^{\frac {433}{250}}={\sqrt[{250}]{5^{433}}}\approx 16.241}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdf754bc1958eba28bd5b9f85aed46c01e62a4d8)























































![{\displaystyle {\begin{aligned}\left(1+i\right)^{i}&=\left[{\sqrt {2}}\left({\frac {\sqrt {2}}{2}}+{\frac {\sqrt {2}}{2}}i\right)\right]^{i}\\&=\left({\sqrt {2}}e^{{\tfrac {\pi }{4}}i}\right)^{i}\\&=e^{-{\tfrac {\pi }{4}}}{\sqrt {2}}^{i}\\&=e^{-{\tfrac {\pi }{4}}}\cos {\frac {\ln 2}{2}}+ie^{-{\tfrac {\pi }{4}}}\sin {\frac {\ln 2}{2}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4f58ca57921434ca075c3ae36a0aecd5cf73f7)






















