哈勃–勒梅特定律
在物理宇宙學裏,哈伯–勒梅特定律(英語:Hubble-Lemaître law)指遙遠星系的退行速度與它們和地球的距離成正比。這條定律原先稱為哈伯定律(英語:Hubble's law),以證實者埃德温·哈勃的名字命名[1];2018年10月经国际天文联合会表决通过更改为现名,以纪念更早发现宇宙膨胀的比利时天文学家乔治·勒梅特[2]。它被認為是空間尺度擴展的第一個觀察依據,今天經常被援引作為支持大爆炸的一個重要證據。
在宇宙学研究中,哈伯-勒梅特定律成为宇宙膨胀理论的基础,以方程式表示
- ;
其中, 是由紅移現象測得的星系遠離速率,是哈伯常數,是星系與觀察者之間的距離。
發現[编辑]
1912年到1922年间,美国天文学家維斯托·斯里弗观测了41个星系的光谱,发现其中的36个星系的光谱发生红移,他认为这种现象意味着这些星系正在远离地球。[3]
1916年,爱因斯坦提出了广义相对论。許多物理學家和數學家利用愛因斯坦場方程建立了時間和空間協調一致的理論。將最一般的原則應用到自然的宇宙,產生了一個動態的解決方案,與當時的靜態宇宙的概念產生了衝突。
1927年,比利时天文学家乔治·勒梅特计算出爱因斯坦场方程的一个解,发现宇宙在不断地膨胀。[4]
1929年,美国天文学家埃德温·哈勃发表其观测结果:距离银河系越远的星系退行越快。
說明[编辑]
因發現遠離速度與距離呈線性關係,而產生哈伯定律,其線性數學式如後:
其中是由紅移現象測得的遠離速率,一般表示為km/s。H0是哈伯常數,在弗里德曼方程式中對應著數值(通常稱為哈伯參數,是一個取決於時間的值,由時間的觀測得來,以下標0來區別。)此常數在宇宙中對任意保角時間(conformal time)而言皆是相同的。是光相對於觀測者的慣性座標系穿越星系的適當距離,以百萬秒差距(Mpc)作為測量單位。
對於相對鄰近的星系,速度v可從星系的紅移z利用紅移公式估計,其中c是光速。對遙遠的星系,速度v可以從紅移z利用相對移動的都卜勒效應決定。然而,最好的方法來計算遠離速度及其相關時空膨脹率是考慮來自遠星系光子的相關保角時間。對於非常遙遠的星體,退離速度可能大於光速。但是這並不違反狹義相對論,因為度量空間的擴張並不與任何有形物體的速度相關。
當使用哈伯定律來決定距離時,只能用因宇宙膨脹而造成的速度。引力相互作用星系的運行與彼此相關,而獨立於宇宙膨脹之外。因其相對運行所造成的這類相對速度,被稱作本動速度(peculiar velocities)。當使用哈伯定律時,本動速度需要加入考慮。1938年,Benjamin Kenneally所發現的「上帝的手指」效應(Fingers of God)是本動速度所造成的現象之一。受引力約束的系統,例如星系或我們的行星系統,都不會受到哈伯定律的影響,也不會膨脹。
針對均勻膨脹的宇宙的理想哈伯定律,其數學推導是一個在三維笛卡爾/牛頓協調空間相當初等的幾何定理。此協調空間被視為一種度量空間,具有完全均勻和各向同性(性質不隨地點或方向改變)。簡單說明該定理如下:
- 對於任何正沿直線遠離原地,速度與離開距離成正比的兩點,將以正比於兩者距離的速度遠離對方。
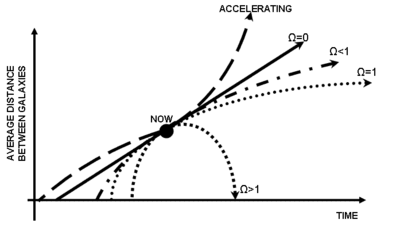
哈伯常數的值隨著時間變化,其增加或減少取決於減速參數的正負,定義為:
在減速參數為零的宇宙,有H = 1/t,其中t是自大霹靂以來的時間。然而,非零且與時間相關的值,則需要積分弗里德曼方程式,將時間倒退到粒子視野(particle horizon)為0時(即大霹靂之初)。
我們可以定義宇宙的「哈伯年齡」(又稱為「哈伯時間」或「哈伯期」)為1/H,或9777.93(億年/[H/(km/s/Mpc)])。哈伯年齡以H=70 km/s/Mpc來計算為139.68億年,或以H=71 km/s/Mpc計算得137.72億年。當星系的紅移z很小時,與我們的距離大約是zc/H,其中c是1(光年/年),又此距離可以被簡單地以z(紅移)時間表示為137.72億光年。
長久以來q被認為是正值,這表示由於引力的作用,宇宙膨脹正在減慢。這意味著宇宙的年齡小於1/H(約140億年)。例如,若q為1/2時(其中一個理論上的可能值),宇宙的年齡為2/(3H) 。在1998年,一項發現指出q顯然是負值,代表著宇宙其實比1/H還要老。事實上,估計的宇宙年齡相當接近1/H。
奧伯斯佯謬[编辑]
哈伯定律對大爆炸的解釋總結了空間的擴展與著名的古老難題奧伯斯佯謬之間的矛盾:如果宇宙是無限的、穩定的,充滿了均勻分布的恆星,那麼在天空中視線所及之處都將存在著恆星,而天空也將會像恆星的表面一樣明亮。從1600年代開始,天文學家和其他的思想家提出了許多可能解決這個佯繆的想法,但當前能被接受的這一部分是來自大爆炸的理論。宇宙只存在了有限的時間,只有有限多的星光有機會到達我們這兒,所以矛盾就解決了。換言之,在膨脹的宇宙中,遠方天體的遠離速度使來自她們的星光產生紅移並且降低了亮度,但這樣也只是解決了部分的矛盾。依照大爆炸的理論,兩者都有貢獻(宇宙的歷史是有限的在兩者中較為重要)。 天空之所以黑暗,也為大爆炸提供了一種證據。[5]
哈伯常數的測量[编辑]
哈伯常數的值通常經由遙遠星系的紅移來測量,這就是用與哈伯定律不同的方法測量同一星系的距離。但是在用來測量這些距離的物理假設上的不確定,造成哈伯常數的值有不同結果的。在20世紀的後半期,多數的哈伯常數值都被估計在50和90 (km/s)/Mpc之間。
對哈伯常數的爭論[编辑]
| “ | 天文物理經常都是錯的,但從未被懷疑過。 ... RP Kirshner[6] | ” |
哈伯常數的值曾是個長久而激烈的爭議主題,熱拉爾·佛科留斯主張其值應為100而艾伦·桑德奇則認為其應為50附近[7]。
1996年,由約翰·諾利斯·巴寇主持,包含古斯塔夫·安德列斯·塔曼及薛尼·范德胡斯特以類似早期沙普利-柯蒂斯之爭的模式舉行,針對上述兩個競爭數值進行辯論。
1990年代晚期,引進宇宙的λ-CDM模型,數值差異的問題獲得部分的解決。
ΛCDM模型[编辑]
在ΛCDM模型下,利用苏尼亚耶夫-泽尔多维奇效应進行的X光高紅移群及微波波長的觀察、宇宙微波背景辐射各向异性的量度和光學調查皆測定哈伯常數的值為67左右[來源請求]。
使用哈伯太空望遠鏡的值[编辑]
哈伯關鍵計畫(由在卡內基天文台的Wendy L. Freedman博士主導)使用哈伯太空望遠鏡進行最精確的光學測量,在2001年五月[8],發表其最終估計值為72±8 (km/s)/Mpc,此結果與基於苏尼亚耶夫-泽尔多维奇效应進行的銀河系星群觀測所測出的相當一致,具有相似的精確值。
使用WMAP的資料[编辑]
在2003年,利用WMAP所得出最高精度的宇宙微波背景辐射測定值為71±4 (km/s)/Mpc,而在2006年,精確度提升至70.4 +1.5
−1.6 (km/s)/Mpc[9],2008年T,WMAP在線上提供的數值是71.9 +2.6
−2.7 (km/s)/Mpc.[1]。
這些來自WMAP和其他宇宙論的數值都與簡單版本的λ-CDM模型日趨接近。如果這些數值能與更普遍的版本吻合,傾向於更小和更不確定:通常數值在67 ± 4 (km/s)/Mpc的附近,但有些模型的數值接近63 (km/s)/Mpc[10]。
使用錢卓X射線天文台的資料[编辑]
在2006年8月,來自馬歇爾太空飛行中心(MSFC)的研究小組使用美國國家航空暨太空總署的錢卓X射線天文台發現的哈伯常數是 77 (km/s)/Mpc,誤差大約是15%[11]。 所有這些測量方法結果的一致性,都支持的值和ΛCDM模型。
加速膨脹[编辑]
在1998年,來自Ia超新星標準燭光測量的值卻是負数,令許多天文學驚訝的是宇宙加速膨脹,雖然哈伯因子會隨著時間而衰減。请參見暗物質和ΛCDM模型。
2009年5月7日,美国宇航局发布最新的哈伯常数测定值,根据对遥远星系Ia超新星的最新测量结果,常数被确定为74.2± 3.6 km/(s*Mpc),不确定度进一步缩小到5%以内。[12]
2012年10月3日,天文学家使用美国宇航局的斯皮策红外空间望远镜精确计算了哈伯常数,数值结果为74.3±2.1(km/s)/Mpc。
2012年12月20日,美國國家航空暨太空總署的威爾金森微波各向異性探測器實驗團隊宣布,哈伯常數為69.32 ± 0.80 (km/s)/Mpc。[13]
2013年3月21日,從普朗克卫星觀測獲得的数据,哈伯常數為67.80 ± 0.77 千米每秒每百万秒差距(67.80 ± 0.77 km/s/Mpc)。[14] [15]
2018年7月,利用哈勃望遠鏡和蓋亞任務,測得哈勃常數值為 73.52 ± 1.62 km s−1 Mpc−1。[16][17]
哈伯常數的推導[编辑]
從弗里德曼方程式開始:
此處是哈伯參數,是宇宙標度因子,是萬有引力常數,是標準化的宇宙空間曲率,其值為 −1、0、或 +1,和是宇宙常數。
物質主導的宇宙(和宇宙常數)[编辑]
如果宇宙是物質主導,則宇宙的質量密度 剛好可以包括的物質是
此處是現在的物質密度,我們知道的非相對論粒子質量密度會隨著宇宙的體積增加而成比例的降低,所以上述方程式必須為真。我們也可以定義(參見的密度參數):
所以也可以,依據定義:
和
此處的下標0代表現在的數值,並且。到此為止的所有一切都是章節剛開始的弗里德曼方程式和轉換 成為 得到
物質和暗能量主導的宇宙[编辑]
如果宇宙是物質主導和暗能量主導,然後前述方程式中的哈伯參數也將是暗能量的狀態方程。所以現在:
此處是暗能量的質量密度。依據定義,在宇宙論的狀態方程是,並且我們將這帶入流體的方程,它描述了宇宙的質量密度隨著時間的變化,
如果w 是常數,
那麼暗能量就是w狀態的恆等式,。如果我們以與之前相似的方式轉換弗里德曼方程,但是這次設定,這是假設我們生活在一個平坦空間的宇宙 (參見宇宙的形狀),
如果暗能量不是w狀態的恆等式,則
要解此方程式,我們需要參數化,例如如果 ,得到
由哈伯常數導出的單位[编辑]
哈伯時間[编辑]
哈伯常數的單位是時間的倒數,也就是說 ~ 2.29×10−18 s−1。“哈伯時間”定義為。在標準宇宙論模型的哈伯時間是4.35×1017 s 或138億年(Liddle 2003,p.57),"擴張時間尺度"一詞的意思是"哈伯時間"[2](页面存档备份,存于互联网档案馆)。如果的值保持恆定,哈伯時間自然的解釋是電子大小的宇宙增加一個數量級所需要的時間 (因為解dx/dt = x is x = exp(t),此處是在t = 0的任意初始條件下的形狀)。但是,在如上文所述的廣義相對論、暗能量、暴脹等,長時間下的動力學是複雜的。
哈伯長度[编辑]
哈伯長度是宇宙論的距離單位,定義為—光速與哈伯時間的乘積。它相當於42億2800萬秒差距或138億光年(哈伯長度以光年表示的數值,依據定義,等同於哈伯時間以年表示的值)。
哈伯體積[编辑]
哈伯體積有時被定義為共動大小的體積。精確的定義是:有時將其定義為球體半徑為時的體積。有些宇宙論甚至使用哈伯體積一詞引用為可觀測宇宙的體積,然而這個半徑可能還要大3倍。
參見[编辑]
| 維基教科書中的相關電子教程:哈勃图:製作 |
參考資料[编辑]
- ^ Hubble, Edwin, "A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae (页面存档备份,存于互联网档案馆)" (1929) Proceedings of the National Academy of Sciences of the United States of America, Volume 15, Issue 3, pp. 168-173 (Full article (页面存档备份,存于互联网档案馆), PDF)
- ^ Move over, Hubble: Discovery of expanding cosmos assigned to little-known Belgian astronomer-priest. Science AAAS. 2018-10-29 [2018-11-02]. (原始内容存档于2020-11-09) (英语).
- ^ 比起哈勃定律的名字 这个常数更让科学家头疼-新华网. www.xinhuanet.com. [2018-11-01]. (原始内容存档于2020-09-15).
- ^ 哈勃定律更名引发学界争议—新闻—科学网. news.sciencenet.cn. [2018-11-01]. (原始内容存档于2020-09-15).
- ^ S. I. Chase, Olbers' Paradox, entry (页面存档备份,存于互联网档案馆) in the Physics FAQ; see also I. Asimov, "The Black of Night", in Asimov on Astronomy (Doubleday, 1974), ISBN 978-0-385-04111-9.
- ^ Quoted by RP Kirshner
- ^ Dennis Overbye, Lonely Hearts of the Cosmos: The Scientific Quest for the Secret of the Universe, Harper-Collins (1991), ISBN 978-0-06-015964-1 & ISBN 978-0-330-29585-7 (finalist, Nation Book Critics Circle Award for non-fiction). Second edition (with new afterword), Back Bay, 1999. Gives an account of the history of the dispute and rivalries.
- ^ W. L. Freedman, B. F. Madore, B. K. Gibson, L. Ferrarese, D. D. Kelson, S. Sakai, J. R. Mould, R. C. Kennicutt, Jr., H. C. Ford, J. A. Graham, J. P. Huchra, S. M. G. Hughes, G. D. Illingworth, L. M. Macri, P. B. Stetson. Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. The Astrophysical Journal. 2001, 553 (1): 47–72 [2006-12-21]. doi:10.1086/320638. (原始内容存档于2016-06-03).. Preprint available here (页面存档备份,存于互联网档案馆).
- ^ D. N. Spergel; et al. Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology. Astrophysical Journal Supplement Series. 2007, 170: 377–408. doi:10.1086/513700.; available online at LAMBDA (页面存档备份,存于互联网档案馆)
- ^ Results for and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA's LAMBDA website (页面存档备份,存于互联网档案馆).
- ^ Chandra independently determines Hubble constant (页面存档备份,存于互联网档案馆) in Spaceflight Now錢卓X射線天文台獨立測出哈伯常數的新聞刊登在「Spaceflight Now」網站
- ^ Refined Hubble Constant Narrows Possible Explanations for Dark Energy (页面存档备份,存于互联网档案馆)精确测定哈伯常数—逼近暗能量的实质
- ^ Bennett, C. L.; et al, Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. (PDF), arXiv:1212.5225, December 10, 2012 [Feb 3, 2013], (原始内容存档 (PDF)于2020-09-18)
- ^ Ade, P. A. R.; Aghanim, N.; Armitage-Caplan, C.; et al. (Planck Collaboration). Planck 2013 results. I. Overview of products and scientific results. Astronomy & Astrophysics (submitted) (arXiv:1303.5062). 20 March 2013 [2013-03-23]. (原始内容存档于2015-09-10).,table 9
- ^ Clavin, Whitney; Harrington, J.D. Planck Mission Brings Universe Into Sharp Focus. NASA. 21 March 2013 [21 March 2013]. (原始内容存档于2013-04-07).
- ^ 科学家完成对哈勃常数至今最精确测量. www.solidot.org. [2018-08-14]. (原始内容存档于2020-09-18).
- ^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; Bucciarelli, Beatrice; Lattanzi, Mario G.; MacKenty, John W.; Bowers, J. Bradley; Zheng, WeiKang. Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant. The Astrophysical Journal. 2018, 861 (2): 126. ISSN 0004-637X. doi:10.3847/1538-4357/aac82e (英语).
來源[编辑]
- Kutner, Marc. Astronomy: A Physical Perspective. Cambridge University Press. 2003. ISBN 978-0-521-52927-3.
- Hubble, E.P.., The Observational Approach to Cosmology (Oxford, 1937)
- http://www.guokr.com/article/436836/(页面存档备份,存于互联网档案馆)
外部連結[编辑]
- History of Hubble's constant(页面存档备份,存于互联网档案馆) by John Huchra
- The Hubble Key Project(页面存档备份,存于互联网档案馆)
- Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant(页面存档备份,存于互联网档案馆). Freedman et. al. The Astrophysical Journal, Volume 553, Issue 1, pp. 47-72.
- The Hubble Diagram Project(页面存档备份,存于互联网档案馆)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||










































