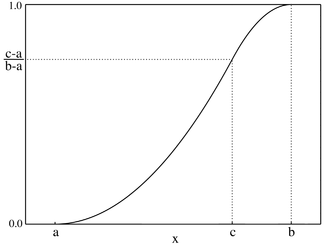
在概率论与统计学中,三角形分布是低限为 a、众数为 c、上限为 b 的连续概率分布。

已知两点[编辑]
当 c=a 或者 c=b,分布就可以进行简化。例如,如果 a=0、b=1 并且 c=1,那么上面的方程简化为:


两个标准一致变量的分布[编辑]
a=0、b=1 且 c=0.5 的分布为  ,其中
,其中  是两个連續型均勻分佈的随机变量。
是两个連續型均勻分佈的随机变量。



三角形分布的应用[编辑]
三角形分布通常用于表述只有有限采样数据的人口信息,尤其是已知变量之间的关系但是由于数据的收集成本太高而缺少采样数据的场合。
这通常是根据已知最小值与最大值从而推算合理的常见值。
商务模拟[编辑]
三角形分布经常用于商务决策,尤其是计算机模拟领域。通常,如果对结果的概率分布所知信息很少,例如仅仅知道最大值与最小值,那么可以使用平均分布模型。但是,如果已经知道了最可能出现的结果,那么就可以用三角形分布进行模拟。
项目管理[编辑]
三角形分布以及Beta分布在项目管理中大量地用作项目评估与审核技术以及关键途径的输入信息,以建立在最大值与最小值之间事件发生的概率模型。
外部链接与参考文献[编辑]