 物理学中通常使用的球坐标(r, θ, φ) (ISO 约定):徑向距離r,极角θ(theta)与方位角φ(phi)。
物理学中通常使用的球坐标(r, θ, φ) (ISO 约定):徑向距離r,极角θ(theta)与方位角φ(phi)。
 数学中通常使用的球坐标(r, θ, φ) :徑向距離r,方位角θ(theta)与极角φ(phi)。
数学中通常使用的球坐标(r, θ, φ) :徑向距離r,方位角θ(theta)与极角φ(phi)。
球座標系(英語:spherical coordinate system)是數學上利用球座標 表示一個點P在三維空間的位置的三維正交座標系。右圖顯示了球座標的幾何意義:原點與點P之間的“徑向距離”(radial distance)
表示一個點P在三維空間的位置的三維正交座標系。右圖顯示了球座標的幾何意義:原點與點P之間的“徑向距離”(radial distance) ,原點到點P的連線與正z-軸之間的“极角”(polar angle)
,原點到點P的連線與正z-軸之間的“极角”(polar angle) ,以及原點到點P的連線在xy-平面的投影線,與正x-軸之間的“方位角”(azimuth angle)
,以及原點到點P的連線在xy-平面的投影線,與正x-軸之間的“方位角”(azimuth angle) 。它可以被视为极坐标系的三维推廣。球座標的概念,延伸至高維空間,則稱為超球座標。
。它可以被视为极坐标系的三维推廣。球座標的概念,延伸至高維空間,則稱為超球座標。
符号约定[编辑]
在學術界內,關於球座標系的標記有好幾個不同的約定。按照國際標準化組織建立的約定(ISO 31-11),球坐標標記為 ,其中
,其中 代表徑向距離,
代表徑向距離, 代表極角,
代表極角, 代表方位角,極角也稱為倾斜(inclination)角、法线角或天頂(zenith)角。這種標記通常為物理界的學者所採用,在世界各地有許多使用者,本條目採用的是物理學界標記約定。方位角(azimuth)、高度(altitude或elevation)角和天頂的概念出自關於天球的地平坐標系。在極坐標系中,角度坐標
代表方位角,極角也稱為倾斜(inclination)角、法线角或天頂(zenith)角。這種標記通常為物理界的學者所採用,在世界各地有許多使用者,本條目採用的是物理學界標記約定。方位角(azimuth)、高度(altitude或elevation)角和天頂的概念出自關於天球的地平坐標系。在極坐標系中,角度坐標 常被稱為極角[1]。
常被稱為極角[1]。
在數學界,球座標標記也是 ,但倾斜角與方位角的標記正好相反:
,但倾斜角與方位角的標記正好相反: 代表方位角,
代表方位角, 代表倾斜角。數學界的標記被認為“提供了對常用的極坐標系記號的邏輯擴展,
代表倾斜角。數學界的標記被認為“提供了對常用的極坐標系記號的邏輯擴展, 仍是在xy-平面上的角度而
仍是在xy-平面上的角度而 是在這個平面之外的角度”[2];一些作者将倾斜角列在方位角之前而写为
是在這個平面之外的角度”[2];一些作者将倾斜角列在方位角之前而写为 ,还有作者对径向距离使用
,还有作者对径向距离使用 而写为
而写为 或
或 [2]。
[2]。
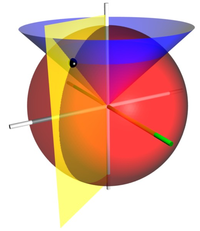 球座標系的幾個座標曲面。紅色圓球面的
球座標系的幾個座標曲面。紅色圓球面的 。藍色圓錐面的
。藍色圓錐面的 。黃色半平面的
。黃色半平面的 (黃色半平面與xz-半平面之間的二面角角度是
(黃色半平面與xz-半平面之間的二面角角度是 )。z-軸是垂直的,以白色表示。x-軸以綠色表示。三個座標曲面相交於點P(以黑色的圓球表示)。直角座標大約為
)。z-軸是垂直的,以白色表示。x-軸以綠色表示。三個座標曲面相交於點P(以黑色的圓球表示)。直角座標大約為 。
。
假設P點在三維空間的位置的三個座標是 。那麼,0 ≤ r是從原點到P點的距離,0 ≤ θ ≤ π是從原點到P點的連線與正z-軸的夾角,0 ≤ φ < 2π是從原點到P點的連線在xy-平面的投影線,與正x-軸的夾角。
。那麼,0 ≤ r是從原點到P點的距離,0 ≤ θ ≤ π是從原點到P點的連線與正z-軸的夾角,0 ≤ φ < 2π是從原點到P點的連線在xy-平面的投影線,與正x-軸的夾角。
這裏, 代表倾斜角,
代表倾斜角, 代表方位角。當
代表方位角。當  時,
時, 與
與 都一起失去意義。當
都一起失去意義。當 或
或 時,
時, 失去意義。
失去意義。
如想要用球座標,找出點P在空間的地點,可按照以下步驟:
- 從原點往正z-軸移動
 單位,
單位,
- 用右手定則,大拇指往y-軸指,x-軸與z-軸朝其他手指的指向旋轉
 角值,
角值,
- 用右手定則,大拇指往z-軸指,x-軸與y-軸朝其他手指的指向旋轉
 角值。
角值。
座標系變換[编辑]
三維空間裏,有各種各樣的座標系。球座標系只是其中一種。球座標系與其他座標系的變換需要用到特別的方程式。
直角座標系[编辑]
使用以下等式,可從直角座標變換為球座標:
 ,
, ,
, 。
。- 計算
 時:
時:
- 1. 必須依照
 所處的象限來計算正確的反正切值。
所處的象限來計算正確的反正切值。
- 2. 當
 時,判斷
時,判斷  的值:
的值:
- 若
 ,則
,則  ,
,
- 若
 ,則
,則  或
或  ,
,
- 若
 ,則
,則  為未定值 ( 因為
為未定值 ( 因為  為未定式 )。
為未定式 )。
反過來,也可從球座標變換為直角座標:
 ,
, ,
, 。
。
圓柱座標系[编辑]
 用圓柱座標來表示一個點的位置
用圓柱座標來表示一個點的位置
圓柱座標系是極座標系在三維空間往z-軸的延伸。 座標用來表示高度。使用以下方程式,可以從圓柱座標
座標用來表示高度。使用以下方程式,可以從圓柱座標 變換為球座標:
變換為球座標:
 、
、 、
、 。
。
反過來,可以從球座標變換為圓柱座標:
 、
、 、
、 。
。
球坐标系下的微积分公式[编辑]
假定 是從原點到P點的連線與正z-軸的夾角,球座標系的標度因子分別為:
是從原點到P點的連線與正z-軸的夾角,球座標系的標度因子分別為:
 、
、 、
、 。
。

微分公式:
- 线元素是一个从
 到
到 的无穷小位移,表示为公式:
的无穷小位移,表示为公式:
 ;
;- 其中的
 是在
是在 的各自的增加的方向上的单位矢量。
的各自的增加的方向上的单位矢量。
- 面积元素1:在球面上,固定半径,天顶角从
 到
到 ,方位角从
,方位角从 到
到 变化,公式为:
变化,公式为:
 。
。
- 面积元素2:固定天顶角
 ,其他两个变量变化,則公式为:
,其他两个变量变化,則公式为:
 。
。
- 面积元素3:固定方位角
 ,其他两个变量变化,則公式为:
,其他两个变量变化,則公式为:
 。
。
- 体积元素,徑向座標从
 到
到 ,天顶角从
,天顶角从 到
到 ,并且方位角从
,并且方位角从 到
到 的公式为:
的公式为:
 。
。
微分算子,如 、
、 、
、 、
、 ,都可以用
,都可以用 座標表示,只要將標度因子代入在正交座標系條目內對應的一般公式,即可得到如下公式:
座標表示,只要將標度因子代入在正交座標系條目內對應的一般公式,即可得到如下公式:
 。
。
 。
。
 。
。
 。
。
地理座標系[编辑]
 地理坐標系,当采用球面时地心纬度
地理坐標系,当采用球面时地心纬度 和大地纬度
和大地纬度 一致。
一致。
地理座標系是自古以來主要用於地理學的另一種版本的球座標系。地理座標標记为 ,其中
,其中 表示方位角並稱為經度,
表示方位角並稱為經度, 表示高度角並稱為地心纬度,
表示高度角並稱為地心纬度, 表示相對高度。在地理學裏,通常不直接使用表示到地心距離的絕對高度,日常中所用地圖中可能不標示任何高度。
表示相對高度。在地理學裏,通常不直接使用表示到地心距離的絕對高度,日常中所用地圖中可能不標示任何高度。
緯度 的定義域是
的定義域是 ,以赤道為緯度
,以赤道為緯度 ,正值往北負值往南。使用以下公式,可從關於天極的天頂角
,正值往北負值往南。使用以下公式,可從關於天極的天頂角 變換為地心緯度
變換為地心緯度 :
:
 ,正值可稱北緯,負值去負號可稱南緯。
,正值可稱北緯,負值去負號可稱南緯。
經度 的定義域是
的定義域是 。設定經過倫敦格林維治天文台的子午線為經度
。設定經過倫敦格林維治天文台的子午線為經度 ,正值往東或負值往西。使用以下公式,可從在赤道參考平面上的方位角
,正值往東或負值往西。使用以下公式,可從在赤道參考平面上的方位角 變換為經度
變換為經度 :
:
 :
: ,正值可稱東經,
,正值可稱東經, :
: ,負值去負號可稱西經。
,負值去負號可稱西經。
東經和西經都有180°經線,二者等同並有關於國際日期變更線。
采用扁椭球时,一般采用椭球面一点的法线与赤道参考平面交角为高度角并称为大地纬度,而地心纬度 和大地纬度
和大地纬度 的关系为:
的关系为:
 ,
,
径向距离即到地心距离 是关于地心纬度
是关于地心纬度 的函数:
的函数:
 ,
,
其中 为参考椭球体的半长轴,
为参考椭球体的半长轴, 为半短轴,
为半短轴, 为偏心率。采用球面时径向距离
为偏心率。采用球面时径向距离 是固定值,地心纬度
是固定值,地心纬度 和大地纬度
和大地纬度 一致。
一致。
正如二維直角座標系專精在平面上,二維球座標系可以很簡易的設定圓球表面上的點的位置。在這裏,我們認定這圓球是個單位圓球;其半徑是1。通常我們可以忽略這圓球的半徑。在解析旋轉矩陣問題上,這方法是非常有用的。
球座標系適用於分析一個對稱於點的系統。舉例而言,一個圓球,其直角座標方程式為 ,可以簡易的用球座標系
,可以簡易的用球座標系 來表示。
來表示。
用來描述與分析擁有球狀對稱性質的物理問題,最自然的座標系,莫非是球座標系。例如,一個具有質量或電荷的圓球形位勢場。兩種重要的偏微分方程式,拉普拉斯方程與亥姆霍茲方程,在球座標裏,都可以成功的使用分離變數法求得解答。這種方程式在角部分的解答,皆呈球諧函數的形式。























































































