相空间表述
| 系列条目 |
| 量子力学 |
|---|
相空间表述是量子力学的一种表述。在这一表述中,系统的状态是在相空间中描述的,位置与动量被放在同等重要的位置。在量子力学常用的薛定谔绘景中则只会采用动量表象或是位置表象中的一种[a]。相空间表述两个关键的特点是:量子态是以准概率分布描述的而非波函数、态矢或是密度矩阵;算符间的乘法被穆瓦亚尔积取代。
相空间表述理论是由希尔布兰德·格伦尼伍尔德于1946年在其博士学位论文中提出的[1]。何塞·恩里科·穆瓦亚尔也在3年后独立导出该理论[2]。他们所提出的理论都建构于赫尔曼·外尔[3]以及尤金·维格纳[4]早先的构想。
相空间表述的主要优势在于其在形式上与哈密顿力学近似,可以避免引入算符,进而可以“令量子化问题摆脱希尔伯特空间的限制”[5]。这一表述具有统计性质,表现了量子力学和经典统计力学逻辑上的联系,提供了一个比较二者的角度[b]。相空间表述在量子光学[c]、量子退相干以及一些特殊问题中已经得到应用,但其尚未得到广泛应用[6]。
相空间表述所基于的一些概念目前已在数学领域得到了进一步发展,如代数形变理论[d]以及非交换几何。
相空间分布
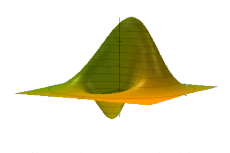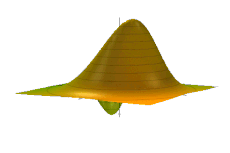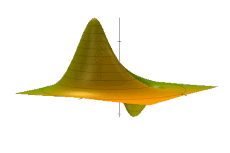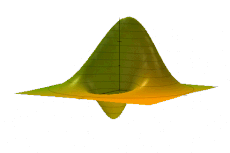
[编辑]在相空间表述中,相空间分布,而非较为常见的波函数或是密度矩阵,是对于系统量子态最为基础的描述方式。量子态f(x,p)在相空间中的分布是一个准概率分布。[7]
这一分布有许多种表象,而这些表象也是互相相关的[8][9]。其中较为重要的一种是維格納準概率分佈表象,W(x,p)[4] 。其他表象包括格劳伯-苏德尔辛P表象[10][11]、伏見Q表象[12]、柯克伍德-雷阿切克表象、梅塔表象、里维耶表象以及玻恩-约当表象等等[13][14][15]。其他表象在哈密顿算符取特定形式时会较为便利,如哈密顿算符取正规序时,采用格劳伯-苏德尔辛P表象在演算时会较为简便。由于维格纳表象较为常用,因而在下文中,如不特殊提及,将统一采用该表象。
相空间分布性质与2n维相空间概率密度分布类似。例如,其分布值是实数,这与通常是复数的波函数不同。我们可以通过在全动量域以及某一位置区间上的维格纳函数积分来理解该位置附近的概率分布:
如果Â(x,p)是一个表征可观测量的算符,其可以通过维格纳变换映射到相空间中,成为A(x, p),还可以通过外尔变换还原回来。
需要注意的是,尽管形式存在一定的类似性,但考虑到概率第三公理的要求W(x,p)并非一种联合分布,因为其所表征的区域中的状态并不一定相互排斥。此外,尽管会违反概率第一公理,即使系统处于纯态时,在特殊情况下,如系统处于相干态[e]时,其值也可能为负。
可以证明,分布值为负的区域非常小,其对于系统整体的影响在几ħ内,因而会在经典极限情况时会消失。但由不确定性原理,负分布值的区域有存在的可能性。不确定性原理并不允许对于相空间内小于ħ的区域进行精确描述。如果方程左边为希尔伯特空间中算符的期望值,那么在量子光学领域,这个式子可以称作光学等价性定理。
星积
[编辑]相空间中基础的二元非交换运算为穆瓦亚尔积,其对应标准的算符间乘法,以符号★表征,因而也称“星积”[1]。每种表象下,相空间分布所对应的星积运算法则也有所不同。下文中将讨论维格纳-外尔表象下的星积。
为了简洁表记,在这里引入左导数与右导数的标记方法。对于一对函数f与g,它们的左、右导数分别定义为:
星积的微分定义为:
式中,指数函数可以理解为一个幂级数。引入额外的微分关系可以令此式的表述形式发生变化:
- 。
能量的本征态分布一般称作“星积本征态”或是“星积本征函数”,对应的能量值则被称为“星积本征值”。它们是对应含时薛定谔方程的星积本征值方程的解[18][19]:
式中H为哈密顿量。它是一个普通相空间函数,通常与经典力学中的哈密顿量相同。
时间演化
[编辑]相空间的时间演化可以通过对刘维尔方程进行量子改造得到[2][9][20]。这个方程是通过对冯诺伊曼方程进行维格纳变换得到的。
对于相空间分布的任意表象及其对应的星积,存在:
特别地,对于维格纳函数,存在:
式中{{ , }}为穆瓦亚尔括号。其为对易算符经过维格纳变换后的结果,而{ , }则为经典力学中的泊松括号。[2]
而这个式子也服从对应原理:当ħ → 0时,这个方程将还原为经典力学中的刘维尔方程。然而,推广至量子流情况时,相空间某一点的密度却并不守恒,概率流也将发散且可压缩。[2]因而在这里,量子轨道的概念会显得有些微妙。[g]
例子
[编辑]简单谐振子
[编辑]
维格纳-外尔表象下,一维简单谐振子的哈密顿量为:
则静态维格纳函数的星积本征值方程为:
首先考察星积本征值方程的虚数部分:
这意味着,星积本征态可以表示为一个单自变量函数:
通过这一变量变换,星积本征值方程的实数部分可以写为一个改造过的拉盖尔方程。它的解可以以拉盖尔多项式的形式表示为[19][1]:
对应的星积本征值为:
对于谐振子而言,任意的维格纳分布的时间演化非常容易求得。初态为W(x,p; t=0) = F(u)时的情况可以通过将上述结果在相空间中做刚性转动求得[1]:
一般情况下,能量E ≫ ħω的量子谐振子可以表征宏观谐振子。其在相空间中会做匀速运动。对其在全相空间中积分(起点为t = 0),则可以得到一个连续的“围栏”。其含时属性与上面的静态星积本征态F(u)相似,可以作为经典极限的直观表现[6]。
自由粒子角动量
[编辑]假设粒子最初处于最小不确定高斯态,位置与动量的期望值在相空间原点。这种自由传播的态的维格纳函数为:
式中,α为表征高斯波包的宽度的参数,而τ = m/α2ħ。
最初,位置与动量并不相关。因而在三维情形下,位矢与动量是平行的,且大小为垂直情形的2倍。
然而,位置与动量的相关性会随着状态演化而越来越强,因为相对于原点传播得越远,动量值需要更大。这一情形的渐近式为[h]:
在这里,只能求出粒子的动能的渐近解,与给定取向独立性时的基态非零角动量情况一致[24]:
莫尔斯势
[编辑]莫尔斯势常被用来近似双原子分子的振动结构。
量子隧穿效应
[编辑]量子隧穿效应是一种典型的量子效应。在发生隧穿时,粒子在不具备足够飞跃势垒的能量时,仍能像有一个“隧道”一样穿过势垒。这一效应在经典力学中并没有对应的效应。
四次势
[编辑]注释
[编辑]参考文献
[编辑]- ^ 1.0 1.1 1.2 1.3 Groenewold, H. J. On the principles of elementary quantum mechanics. Physica. 1946, 12 (7): 405–460. doi:10.1016/S0031-8914(46)80059-4 (英语).
- ^ 2.0 2.1 2.2 2.3 2.4 Moyal, J. E. Quantum mechanics as a statistical theory. Mathematical Proceedings of the Cambridge Philosophical Society (Cambridge University Press). 1949, 45 (01): 99–124. doi:10.1017/S0305004100000487 (英语).
- ^ Weyl, H. Quantenmechanik und gruppentheorie. Zeitschrift für Physik. 1927, 46 (1-2): 1–46. doi:10.1007/BF02055756 (德语).
- ^ 4.0 4.1 Wigner, E. On the quantum correction for thermodynamic equilibrium. Physical Review. 1932, 40 (5): 749–759. doi:10.1103/PhysRev.40.749 (英语).
- ^ Ali, S. T.; Engliš, M. Quantization methods: a guide for physicists and analysts. Reviews in Mathematical Physics. 2005, 17 (04): 391–490. doi:10.1142/S0129055X05002376 (英语).
- ^ 6.0 6.1 Curtright, T. L.; Zachos, C. K. Quantum Mechanics in Phase Space. Asia Pacific Physics Newsletter. 2012, 1: 37. doi:10.1142/S2251158X12000069 (英语).
- ^ 7.0 7.1 Zachos, C.; Fairlie, D.; Curtright, T. Quantum mechanics in phase space: an overview with selected papers. World Scientific. 2005. ISBN 978-981-238-384-6 (英语).
- ^ Cohen, L. Generalized Phase-Space Distribution Functions. Journal of Mathematical Physics. 1966, 7 (5): 781. Bibcode:1966JMP.....7..781C. doi:10.1063/1.1931206 (英语).
- ^ 9.0 9.1 Agarwal, G. S.; Wolf, E. Calculus for functions of noncommuting operators and general phase-space methods in quantum mechanics. II. Quantum mechanics in phase space. Physical Review D. 1970, 2 (10): 2187–2205. doi:10.1103/PhysRevD.2.2187 (英语).
- ^ Sudarshan, E. C. G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Physical Review Letters. 1963, 10 (7): 277–279. doi:10.1103/PhysRevLett.10.277 (英语).
- ^ Glauber, R. J. Coherent and incoherent states of the radiation field. Physical Review. 1963, 131 (6): 2766–2788. doi:10.1103/PhysRev.131.2766 (英语).
- ^ Husimi, K. Some formal properties of the density matrix. Nippon Sugaku-Buturigakkwai Kizi Dai 3 Ki. 1940, 22 (4): 264–314 (英语).
- ^ Agarwal, G. S.; Wolf, E. Calculus for functions of noncommuting operators and general phase-space methods in quantum mechanics. I. Mapping theorems and ordering of functions of noncommuting operators. Physical Review D. 1970, 2 (10): 2161–2186. doi:10.1103/PhysRevD.2.2161 (英语).
- ^ Cahill, K. E.; Glauber, R. J. Ordered expansions in boson amplitude operators. Physical Review. 1969, 177 (5): 1857–1881. doi:10.1103/PhysRev.177.1857 (英语).
- ^ Cahill, K. E.; Glauber, R. J. Density operators and quasiprobability distributions. Physical Review. 1969, 177 (5): 1882–1902. doi:10.1103/PhysRev.177.1882 (英语).
- ^ Lax, M. Quantum Noise. XI. Multitime correspondence between quantum and classical stochastic processes. Physical Review. 1968, 172 (2): 350–361. doi:10.1103/PhysRev.172.350 (英语).
- ^ Baker Jr., G. A. Formulation of quantum mechanics based on the quasi-probability distribution induced on phase space. Physical Review. 1958, 109 (6): 2198–2206. doi:10.1103/PhysRev.109.2198 (英语).
- ^ Fairlie, D. B. The formulation of quantum mechanics in terms of phase space functions. Mathematical Proceedings of the Cambridge Philosophical Society. 1964, 60 (3): 581. doi:10.1017/S0305004100038068 (英语).
- ^ 19.0 19.1 Curtright, T.; Fairlie, D.; Zachos, C. Features of time-independent Wigner functions. Physical Review D. 1998, 58 (2). Bibcode:1998PhRvD..58b5002C. arXiv:hep-th/9711183
 . doi:10.1103/PhysRevD.58.025002 (英语).
. doi:10.1103/PhysRevD.58.025002 (英语).
- ^ Mehta, C. L. Phase‐Space Formulation of the Dynamics of Canonical Variables. Journal of Mathematical Physics. 1964, 5 (5): 677–686. doi:10.1063/1.1704163 (英语).
- ^ Marinov, M. S. A new type of phase-space path integral. Physics Letters A. 1991, 153 (1): 5-11 [2016-01-29]. (原始内容存档于2015-09-24) (英语).
- ^ Krivoruchenko, M. I.; Faessler, A. Weyl’s symbols of Heisenberg operators of canonical coordinates and momenta as quantum characteristics. Journal of mathematical physics. 2007, 48 (5): 052107. doi:10.1063/1.2735816 (英语).
- ^ Curtright, T. L. Time-dependent Wigner Functions. Department of Physics, College of Arts & Sciences, University Miami. [2016-01-29]. (原始内容存档于2020-10-27) (英语).
- ^ Dahl, J. P.; Schleich, W. P. Concepts of radial and angular kinetic energies. Physical Review A. 2002, 65 (2): 022109. doi:10.1103/PhysRevA.65.022109 (英语).
| ||||||||||||||||||||||||||||


![{\displaystyle \operatorname {P} [a\leq X\leq b]=\int _{a}^{b}\int _{-\infty }^{\infty }W(x,p)\,dp\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/219e9896ba7470a2a24afc69c241fcab881d41c8)


















![{\displaystyle W\longrightarrow {\frac {1}{(\pi \hbar )^{3}}}\exp \left[-\alpha ^{2}\left(\mathbf {x} -{\frac {\mathbf {p} t}{m}}\right)^{2}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4de73a30048e75e3a860e81b23c47ea7ce95dfb2)



