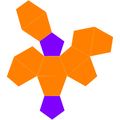
雙五角錐台
 | |||
| 類別 | 雙錐台 對偶詹森多面體 | ||
|---|---|---|---|
| 對偶多面體 | 雙五角錐柱 | ||
| 性質 | |||
| 面 | 12 | ||
| 邊 | 25 | ||
| 頂點 | 15 | ||
| 歐拉特徵數 | F=12, E=25, V=15 (χ=2) | ||
| 組成與佈局 | |||
| 面的種類 | 10個梯形、2個五邊形 | ||
| 對稱性 | |||
| 對稱群 | D5h, [5,2], (*n55) | ||
| 特性 | |||
| 凸多面体 | |||
| 圖像 | |||
| |||
在幾何學中,雙五角錐台是雙錐台的一種,指二個五角錐台底面和底面相接所組成的立體,或是雙五角錐被二個平行平面所截位於二個平面中間的立體圖形。每個雙五角錐台皆有10個梯形和2個五邊形。
結構
這個多面體可以藉由將雙五角錐的上下兩個頂點切去構造。在康威多面體表示法中可以使用「切去五階頂點」或「切去頂點圖為五邊形的頂點」的截角變換構造,即切去該立體所有頂點為五個多邊形的公共頂點之頂點,在康威多面體表示法中以 t5 表示,又因原像是雙五角錐,而雙五角錐是五角柱的對偶,因此在康威多面體表示法中計為 dP5,其中d表示對偶多面體、P5表示五角柱。因此整個雙五角錐台在康威多面體表示法中計為t5dP5[1][2]。
其他雙五角錐台
雙五角錐台也可以藉由將兩個五角錐台底面對底面的組合來構造。對於這類構造方式,雙五角錐台一般都是較大的底面互相接合所形成的凸多面體,若是由較小的底面接合的話,則會變成凹多面體,然而這種多面體也是雙五角錐台,但是其與一般的雙五角錐台不同,不能藉由雙五角錐切去上下的頂點構造。
對偶多面體
雙五角錐台的對偶多面體是雙五角錐柱,是92種詹森多面體中的其中一個,其編號為J16,它可由一個正五角柱在兩端各連接一個正多面體大小相同的五角錐面接合而成,與雙五角錐(J12)有一定的相似程度。這92種詹森多面體最早在1996年由諾曼詹森命名並給予描述[3]。
雙五角錐台的對偶為十五面體,具有15個面:10個三角形和5個正方形,20個邊和10個頂點。
| 雙五角錐台 的對偶多面體 |
對偶的展開圖 |
|---|---|

|

|
應用
在準晶的形成中,15個頂點的雙五角錐台結構可以從大的五次對稱或二十面體對稱成核而得[4]。
相關多面體
雙五角錐台是由雙五角錐被二個平面所截所形成的立體,與其相關的平截頭體包括雙五角錐只被一個平面所截形成的五角錐台錐,與五角錐柱或五角錐以不同方式截出的平截頭體。
五角錐台錐
在幾何學中,五角錐台錐是一種將五角錐台與五角錐底面對底面相接的立體,或是與用一個平面截雙五角錐後得到二個立體,一個是五角錐,另一個就是五角錐台錐。 五角錐台錐為自身對偶,具有11個面、20個邊和11個頂點,其可以為詹森多面體正五角錐柱的對偶,由於大部分的五角錐台錐為自身對偶,而正五角錐柱這種詹森多面體屬於五角錐台錐中的特例,但他們都具有相同的拓樸結構。拓樸結構有明顯差異意味著兩種多面體無法透過移動頂點位置、扭曲或伸縮來相互變換的多面體,例如五角錐台錐和雙五角錐台,無論如何變形都無法互相變換,因此拓樸結構不同,但五角錐台錐和五角錐柱可以透過伸縮其中一個五角形面來彼此互換,因此五角錐台錐和五角錐柱在拓樸上並無明顯差異。
五角錐台錐也是正五角錐柱的對偶,是一種十一面體,具有11個面:5個等腰三角形、5個等腰梯形和一個正三角形。
五角錐台
 | ||||
| 類別 | 錐台 | |||
|---|---|---|---|---|
| 對偶多面體 | 上下不對稱的雙五角錐 | |||
| 性質 | ||||
| 面 | 7 | |||
| 邊 | 15 | |||
| 頂點 | 10 | |||
| 歐拉特徵數 | F=7, E=15, V=10 (χ=2) | |||
| 組成與佈局 | ||||
| 面的種類 | 5個梯形,2個五邊形 | |||
| 對稱性 | ||||
| 對稱群 | C5v, [1,5], (*55) | |||
| 特性 | ||||
| 凸多面体 | ||||
| 圖像 | ||||
| ||||
在幾何學中,五角錐台是一種錐台或平截頭體,五角錐台可以視作雙五角錐台的一半,但更精確的定義為一個五角錐被兩個平行平面所截後,位於兩個平行平面之間的立體。五角錐台雖與雙五角錐台相似,但擁有不同的對稱性,且其對稱性較雙五角錐台低,也不屬於任何一個詹森多面體的對偶多面體。
其他多面體
雙五角錐台是由五角柱先後經過對偶和截角變換而得,五角錐台亦是五角柱變形而來,而五角柱可以視為截角的五面形,五面形又是五邊形二面體的對偶。其他與五邊形二面體相關的多面體除了五角錐台之外,還有:
| 對稱群:[5,2], (*522) | [5,2]+, (622) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|

|

|

| ||||||
| {5,2} | t{5,2} | r{5,2} | 2t{5,2}=t{2,5} | 2r{5,2}={2,5} | rr{5,2} | tr{5,2} | sr{5,2} | ||
| 半正對偶 | |||||||||

|

|

|

|

|

|

| |||
| V52 | V102 | V52 | V4.4.5 | V25 | V4.4.5 | V4.4.10 | V3.3.3.5 | ||
參見
| 3 | 4 | 5 |
|---|---|---|
 雙三角錐台 |
 雙四角錐台 |
 雙五角錐台 |
參考文獻
- ^ 喬治·威廉·哈特. Conway Notation for Polyhedra. [2014-12-20]. (原始内容存档于2014-11-29).
- ^ t5dP5, PolyHédronisme. [2022-08-09].
- ^ Norman W. Johnson, Convex polyhedra with regular faces, 加拿大數學學報, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- ^ Hofmeister, Herbert, Fivefold twinning in nanosized particles and nanocrystalline thin films – ubiquitous metastable structures (PDF), Materials Science Forum: 325–332, [2016-08-30], doi:10.4028/www.scientific.net/MSF.312-314.325, (原始内容存档 (PDF)于2011-05-15).