截半立方体
 (按这里观看旋转模型) | |||||
| 类别 | 半正多面体 | ||||
|---|---|---|---|---|---|
| 对偶多面体 | 菱形十二面体 | ||||
| 识别 | |||||
| 名称 | 截半立方体 | ||||
| 参考索引 | U07, C19, W11 | ||||
| 鲍尔斯缩写 | co | ||||
| 数学表示法 | |||||
| 考克斯特符号 | |||||
| 施莱夫利符号 | t1{4,3} t0,2{3,3} r{4,3} rr{3,3} | ||||
| 威佐夫符号 | 2 | 3 4 3 3 | 2 | ||||
| 康威表示法 | aC aaT | ||||
| 性质 | |||||
| 面 | 14 | ||||
| 边 | 24 | ||||
| 顶点 | 12 | ||||
| 欧拉特征数 | F=14, E=24, V=12 (χ=2) | ||||
| 组成与布局 | |||||
| 面的种类 | 正三角形 正方形 | ||||
| 面的布局 | 8个{3} 6个{4} | ||||
| 顶点图 | 3.4.3.4 | ||||
| 对称性 | |||||
| 对称群 | Oh群 and Th | ||||
| 特性 | |||||
| quasiregular | |||||
| 图像 | |||||
| |||||
在几何学中,截半立方体是一种十四面体,由八个三角形与六个正方形组成,具有14个面、12个顶点以及24条边。是一种阿基米德立体[1],属于半正多面体和拟正多面体。其对偶多面体为菱形十二面体。
性质
[编辑]截半立方体具有十二个结构相等的顶点,皆为两个三角形与两个正方形的公共顶点、24个结构相等的棱,相邻面皆为三角形与正方形,两面角为反正割负根号三[2],约125.26度,因此同时具有点可递和边可递的性质,因此是一种均匀多面体、半正多面体和拟正多面体,并且为阿基米德发现的13种半正多面体之一,因此也属于阿基米德立体。此外,由于截半立方体可以视为立方体和其对偶多面体正八面体中三角形与正方形的组合,因此又是一种立方体和其对偶多面体正八面体的立体混合物。

截半立方体是立方体透过截半变换构造而成的多面体,简而言之是用立方体由一条棱斩到另一条棱的中点(即斩去立方体的顶点)而成。因此其正方形面的数目和立方体的面都为6,其三角形面数目和立方体的顶点数目都为8,共有面14个。因为同样种类的正多边形面棱不相交,故可以计算其边数乘以面的数目来得其棱的数目:3×8=4×6=24。
截半立方体是立方体透过截半变换构造而成的多面体,也可以由对偶——正八面体透过截半变换构成[3],因此也称为截半八面体。
截半立方体每六条棱可以成为一个正六边形,共有四个独立的六边形。
座标
[编辑]一个边长为2的平方根的截半立方体,其顶点座标位于(0, ±1, ±1)、(±1, 0, ±1)、(±1, ±1, 0)[4]的全排列。
体积与表面积
[编辑]表面积,体积,其中是该截半立方体的边长[2]。
- 表面积 =
- 体积 =
作法
[编辑]截半立方体的作法有两种,一种由立方体出发,另外一种由正八面体出发,同样都是透过截半变换来构造。从立方体出发的方法为:将立方体的八个顶点切到一半就可以得到一个截半立方体,而从正八面体出发的作法一样是将顶点切到一半:将正八面体的六个顶点切到一半就可以得到一个截半立方体。
截半立方体的康威多面体记号为aC或aO,由于截半变换的性质,对偶后结伴得到相同结果,即 a = ad ,因此可以得到 aC (截半立方体) = adC = a(dC) = aO (截半八面体)。
另外也可以由编号3的詹森多面体,J3——三角帐塔组成,两个相反并交错堆叠,称为异相双三角帐塔,而另外一种叫做同相双三角帐塔,也是一种詹森多面体,编号J27。
其他名称
[编辑]- 平行十四面体(英语:Heptaparallelohedron),在英语中,Heptaparallelohedron指的是有七组平行面的多面体,Hepta-代表七,Parallelo-代表平行,类似的命名方式例如Parallelogram,指平行四边形。Heptaparallelohedron一词巴克敏斯特·富勒首次使用代表截半立方体。
- 在Oh对称性中,可以称为截半立方体或截半八面体 (诺曼·约翰逊)。
- 在Td对称性中,可以称为小斜方截半四面体。
- 在D3d对称性中,可以称为异相双三角帐塔。
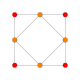
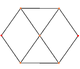
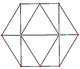
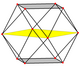
正交投影
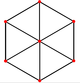
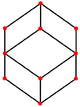
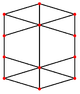
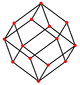
[编辑]| 正方形 面 |
正三角形 面 |
顶点 | 边 | 歪斜 | |
|---|---|---|---|---|---|
|

|
|
|
|

|
| [4] | [6] | [2] | [2] | ||
| 菱形十二面体为截半立方体的对偶 | |||||

|
|
|
|
|
|
球面镶嵌
[编辑]
|
 以正方形为中心 |
 以正三角形为中心 |
| 平行投影 | 施莱格尔投影 | |
|---|---|---|
相关多面体及镶嵌
[编辑]| 对称性: [3,3], (*332) | [3,3]+, (332) | ||||||
|---|---|---|---|---|---|---|---|

|

|

|

|

| |||
| {3,3} | t0,1{3,3} | t1{3,3} | t1,2{3,3} | t2{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} |
| 半正多面体对偶 | |||||||

|

|

|

| ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
也可以由倒角立方体经过特殊的切割方式而得。在切割成截半立方体之前可以得到一些不同的多面体,例如:
| (可能的来源) | 倒角立方体 (截边立方体) |
截角倒角立方体 (截边截角立方体) |
截半倒角立方体 (截边截半立方体) |
截半立方体 | |
|---|---|---|---|---|---|
| 图像 |  菱形十二面体 |
 倒角立方体 |
 小斜方截半立方体 |
 大斜方截半立方体 |
 截半立方体 |
| 考克斯特符号 | |||||
| 对偶多面体 | |||||
| 对偶 |  截半立方体 |
 四角化截半立方体 |
 筝形二十四面体 |
 四角化菱形十二面体 |
 菱形十二面体 |
| 考克斯特符号 | |||||
| 对称性: [4,3], (*432) | [4,3]+, (432) | [1+,4,3], (*332) | [4,3+], (3*2) | ||||||
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|
||||||
| {4,3} | t0,1{4,3} | t1{4,3} | t1,2{4,3} | {3,4} | t0,2{4,3} | t0,1,2{4,3} | s{4,3} | h{4,3} | h1,2{4,3} |
| 半正多面体的对偶 | |||||||||

|

|

|

|

|

| ||||
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
截半立方体图
[编辑]| 截半立方体图 | |
|---|---|
 四阶对称性 | |
| 顶点 | 12 |
| 边 | 24 |
| 自同构群 | 48 |
| 属性 | Quartic graph, Hamiltonian, regular |
在图论的数学领域中,与截半立方体相关的图为截半立方体图,是截半立方体之边与顶点的图,是一种阿基米德图。其共有12个顶点和24条棱,且是四次的阿基米德图[8]。
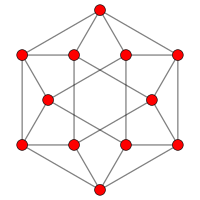 六阶对称性 |
其他领域
[编辑]
|
| 截半立方体是甲烷水合物的一种形式 即甲烷被排列成截半立方体的冰分子包住 |
参见
[编辑]参考文献
[编辑]- ^ Cromwell, P. Polyhedra, CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
- ^ 2.0 2.1 Weisstein, Eric W. (编), Cuboctahedron, (Archimedean solid), at MathWorld--A Wolfram Web Resource,Wolfram Research, Inc. (英语)
- ^ Ghyka, Matila. The geometry of art and life. [Nachdr.] New York: Dover Publications. 1977: 51–56, 81–84. ISBN 9780486235424.
- ^ Weisstein, Eric W. Cuboctahedron. CRC Concise Encyclopedia of Mathematics. 2nd. Hoboken: CRC Press: 620–621. 2002. ISBN 9781420035223.
- ^ 珍.E.霍夫特(Jane E. Hoffelt). 我們住在同一個世界. 大颖【生活学习】. 胡洲贤 译. 大颖. 2009. ISBN 9789866407758. 我们住在同一个世界(培养孩子包容的世界观)~获第32次中小学生优良课外读物推介 互联网档案馆的存档,存档日期2016-02-04. 戴美心地图 [2016-1-27]
- ^ 一般性地图资料代码 (页面存档备份,存于互联网档案馆) 国家图书馆编目 第四页 dg = 戴美克森氏投影 (dimaxion) 2001年10月
- ^ Vector Equilibrium: R. Buckminster Fuller. [2016-01-27]. (原始内容存档于2016-03-08).
- ^ Read, R. C.; Wilson, R. J., An Atlas of Graphs, Oxford University Press: 269, 1998
- Richter, David A., Two Models of the Real Projective Plane, [2016-01-27], (原始内容存档于2016-03-03)
- Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
外部链接
[编辑]- 埃里克·韦斯坦因, 截半立方体 (参阅阿基米德立体) 于MathWorld(英文)
- The Uniform Polyhedra (页面存档备份,存于互联网档案馆)
- Virtual Reality Polyhedra (页面存档备份,存于互联网档案馆) The Encyclopedia of Polyhedra
- Klitzing, Richard. 3D convex uniform polyhedra o3x4o - co. bendwavy.org.
- Editable printable net of a Cuboctahedron with interactive 3D view (页面存档备份,存于互联网档案馆)







































