跳至內容

熱力學

編輯連結
本頁使用了標題或全文手工轉換
維基百科，自由的百科全書
熱力學
經典的卡諾熱機
T（熱庫）、Q（熱量）、W（功）
H（高溫）、C（低溫）
分支
定律
系統
狀態
過程
循環
系統性質
狀態函數
（斜體共軛物理量）
過程函數
材料性質
比熱容 
壓縮性 
熱膨脹 
方程（英語：Thermodynamic equations）
勢
  • 內能
  • 焓
  • 吉布斯能
歷史／文化
哲學
歷史
理論
關鍵著作
年表
科學家
一個典型的熱力學系統，熱從較熱處（鍋爐）流向較冷處（冷凝器），在這一過程中有一系列活塞做了功。

熱力學（法語：thermodynamique，德語：Thermodynamik，英語：thermodynamics，源於古希臘語θερμός及δύναμις），是研究熱現象中物態轉變和能量轉換規律的學科。它著重研究物質的平衡狀態以及與準平衡態的物理、化學過程。熱力學定義許多巨觀的物理量（像溫度、內能、熵、壓強等），描述各物理量之間的關係。熱力學描述數量非常多的微觀粒子的平均行為，其定律可以用統計力學推導而得。

熱力學可以總結為四條定律：

  • 熱力學第零定律定義了溫度這一物理量，指出了相互接觸的兩個系統，熱流的方向。
  • 熱力學第一定律指出內能這一物理量的存在，並且與系統整體運動的動能和系統與環境交互作用的位能是不同的，區分出熱與功的轉換。
  • 熱力學第二定律涉及的物理量是溫度和熵。熵是研究不可逆過程引入的物理量，表徵系統透過熱力學過程向外界最多可以做多少熱力學功。
  • 熱力學第三定律認為，不可能透過有限過程使系統冷卻到絕對零度。

熱力學可以應用在許多科學及工程的領域中，例如：引擎、相變化、化學反應、輸運現象甚至是黑洞。熱力學計算的結果不但對物理的其他領域很重要，對航空工程、航海工程、車輛工程、機械工程、細胞生物學、生物醫學工程、化學、化學工程及材料科學等科學技術領域也很重要，甚至也可以應用在經濟學中[1][2]，另見「熱經濟學」。

熱力學是從18世紀末期發展起來的理論，主要是研究功與熱量之間的能量轉換；在此功定義為力與位移的內積；而熱則定義為在熱力系統邊界中，由溫度之差所造成的能量傳遞。兩者都不是存在於熱力系統內的性質，而是在熱力過程中所產生的。

熱力學的研究一開始是為了提昇蒸汽引擎的效率，早期尼古拉·卡諾有許多的貢獻，他認為若引擎效率提昇，法國有可能贏得拿破崙戰爭[3]。出生於愛爾蘭的英國科學家克耳文在1854年首次提出了熱力學明確的定義[4]：

一開始熱力學研究關注在熱機中工質（如蒸氣）的熱力學性質，後來延伸到化學過程中的能量轉移，例如在1840年科學家傑邁因·亨利·蓋斯提出，有關化學反應的能量轉移的研究[5]。化學熱力學中研究熵對化學反應的影響[6][7][8][9][10][11][12][6][13][14] 。統計熱力學也稱為統計力學，利用根據微觀粒子力學性質的統計學預測來解釋巨觀的熱力學性質。

簡介

[編輯]

熱力學一詞一般是指物體和過程的巨觀描述[15]：「古典熱力學和個別原子的性質無關」[16]。「統計熱力學」會用個別原子的性質來描述物體和過程，主要是將其描述為一群有類似特性的粒子，彼此的機率都相同。

熱力學最早是在研究能量的轉移，藉由巨觀變數可以將能量轉移分為二類：熱和功（英語：Work (thermodynamics)）[17][18]。

熱力學平衡是熱力學中幾個最重要概念中的一個[19]。一個熱力學平衡系統的溫度可以明確定義，可能也是熱力學中最有代表性的物理量。若系統及過程不在熱力學平衡的狀態，就很難進行精確的熱力學研究。不過在工程的應用中，往往會通過簡單的近似計算，用平衡熱力學中的物理量，得到較實用的數值。在許多實際的系統中（例如熱機及冰箱），系統會包括數個有不同溫度和壓強的子系統，若這些子系統的熱力學變數已足夠接近明確定義的情形，就可以用較有效的方法來求解熱力學系統的變數。

熱力學最基礎的概念是系統和環境[20]。一個熱力學系統的環境是與之交互作用的其他熱力學系統。熱力學環境的一個典型例子是熱浴，使系統的溫度維持在某特定值，具體的交互作用形式可不去關心。

熱力學最基本的實體是熱力學狀態和熱力學過程。熱力學中的推理可基於熱力學狀態或熱力學循環過程。

熱力學系統可由其狀態來描述，熱力學系統是個巨觀物理對象，由描述巨觀性質的物理和化學變數描述。所需的巨觀態變數視具體的實驗而定。

熱力學系統可由其所經歷的過程來描述，尤其是循環過程，這也是熱力學創立者所採用的方法。

熱力學和統計熱力學應用於研究某一體系的過程，過程中分子的運動可分為兩類：

  • 快速運動，在所研究的過程的時間尺度上，分子可以遍歷它所有可能的狀態，使體系很快達到熱力學平衡。
  • 慢速運動，在所研究的過程的時間尺度上，可忽略分子運動。[21][22]

如果巨觀過程中，分子運動介於快速運動和慢速運動之間，在所研究的過程的時間尺度上，系統一般處於非平衡態。分離分子運動的時間尺度是熱力學中經常考慮的問題。

例如，古典熱力學主要是研究物質的狀態方程式，巨觀力學量和溫度比環境的變化要快很多，實際上是研究熱力學平衡下的狀態變數。狀態方程式表述的是系統的本構特性。狀態方程式常寫為壓力是體積和溫度的函數。[23][24][25][26]

本條目以由淺入深的方式介紹熱力學，先介紹循環過程和熱力學平衡態，最後介紹熱力學非平衡態。

熱力學史

[編輯]
熱力學始創八學派的代表性科學家
主條目：熱力學史

熱力學史可追溯到1650年格里克設計和建造了世界上第一個真空泵，並用馬德堡半球實驗證明了真空的存在，推翻了亞里斯多德提出的「自然界厭惡真空（英語：Horror vacui (physics)）」的假說。1656年，物理學家和化學家羅伯特·波以耳借鑑格里克的設計，與羅伯特·虎克發明了抽氣機[27]。利用抽氣機，波以耳和虎克證明了壓力、溫度和體積之間有一定的關係，波以耳給出了波以耳定律，對於一定溫度下的一定量的氣體，壓力與體積成反比。1679年，波以耳的助手丹尼斯·帕潘發明了蒸汽蒸煮器，這是一個嚴密封蓋的容器，裡面會產生高壓氣體。帕潘後來對他發明的蒸煮器做了改進，加裝了放氣閥門，避免爆炸。帕潘觀察到了閥門的週期性的運動，構想出活塞和汽缸蒸汽機，但是他沒有去實現自己的想法。1697年，工程師托馬斯·塞維利在帕潘的設計的基礎上，發明了第一個蒸汽機。隨後，1712年，湯瑪斯·紐科門也發明了一種蒸汽機。這些早期的蒸汽機非常粗糙，效率很低，但吸引了當時頂尖的科學家的注意。

1759年，詹姆斯·瓦特開始設計蒸汽機，屢經失敗。瓦特向格拉斯哥大學的教授約瑟夫·布拉克求教。布拉克向其講解了自己提出的熱容和潛熱的概念，瓦特還想出了分離冷凝器的想法，終於顯著提高了蒸汽機的效率[a]。尼古拉·卡諾總結前人工作，在1824年發表著作《論火的動力（英語：Reflections on the Motive Power of Fire）》。這部著作論述了卡諾熱機和卡諾循環的關係。這部著作是熱力學成為現代科學的標誌，卡諾也被稱作熱力學之父。

19世紀50年代，熱力學第一和第二定律同時形成，主要完成者是威廉·約翰·麥夸恩·蘭金、魯道夫·克勞修斯和威廉·湯木生。1859年，史上第一部熱力學教科書出版，作者是蘭金。[28]

統計熱力學的創立者包括：馬克士威、波茲曼、普朗克、克勞修斯、吉布斯。

分支學科

[編輯]

熱力學系統是理論上構建出來，以熱力學定律研究有物質和能量交換的物理系統。熱力學系統的研究可分為幾個分支學科，各自有不同的基本模型，或採用不同的原理。

古典熱力學

[編輯]

古典熱力學用不隨時間改變的平衡態或者連續的循環過程描述和研究熱力學系統。應用的物理量是不隨時間改變的實驗可測量的巨觀平衡態的物理量，即物理量的長時間平均的量不隨時間改變，比如循環過程的流。

局域平衡態熱力學

[編輯]

擴展熱力學

[編輯]

統計熱力學

[編輯]

熱力學定律

[編輯]
  • 熱力學第零定律：在不受外界影響的情況下，只要A和B同時與C處於熱平衡，即使A和B沒有熱接觸，他們仍然處於熱平衡狀態。這個定律說明，互相處於熱平衡的物體之間必然具有相等的溫度。
  • 熱力學第一定律：能量守恆定律對非孤立系統的擴展。此時能量可以以功W或熱量Q的形式傳入或傳出系統。熱力學第一定律表達式為：
  • 熱力學第二定律：孤立系統熵（失序）不會減少──簡言之，熱不能自發的從冷處轉到熱處，而不引起其他變化。任何高溫的物體在不受熱的情況下，都會逐漸冷卻。這條定律說明第二類永動機不可能製造成功。熱力學第二定律也可表示為熵增原理：。
  • 熱力學第三定律：完整晶體於絕對溫度零度時（即攝氏-273.15度），熵增為零。

系統模型

[編輯]
各種熱力學系統中允許的質量或能量交換方式
熱力學系統分類 交換方式
質量 功 熱
開放系統 Green tickY Green tickY
封閉系統 Red XN Green tickY Green tickY
絕熱封閉系統 Red XN Green tickY Red XN
力學封閉系統 Red XN Red XN Green tickY
孤立系統 Red XN Red XN Red XN
熱力學系統的示意圖

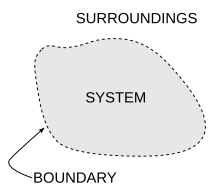
熱力學系統是熱力學的重要概念之一，是指一塊有明確定義的區域，所有不在熱力學系統內的區域合稱為環境，系統和環境之間是由邊界隔開，系統和環境透過邊界才能交換物質、功（英語：Work (thermodynamics)）或熱。

邊界就是包圍系統外圍的表面，任何通過表面，會影響系統內能的都需要在能量平衡方程式中考慮。像馬克斯·普朗克在1900年時的研究就將系統定義為單一原子周圍有共振能量的區域，薩迪·卡諾在1824年將系統定義為蒸汽機中的蒸氣，克里·伊曼紐爾在1986年有關大氣熱力學的研究中將系統定義為熱帶氣旋的本體。在量子統計力學中會將核種（一個由夸克組成的系統）定義為一個系統。

邊界可分為四種：固定、活動、真實、虛構。在引擎中的固定邊界是指活塞固定在某特定位置，因此在等容過程中，不會產生功。而在引擎中的活動邊界是指允許活塞移動位置，因此可以產生功。在封閉系統中，邊界是真實的，而在開放系統中，邊界多半是虛構的。[29]

系統可以依邊界允許的質量或能量交換方式來分類，簡單分類可以分為以下三類：

  • 孤立系統：系統完全不與外界交換能量或質量。
  • 封閉系統：系統只與外界交換能量而不交換質量。
  • 開放系統：系統與外界交換能量和質量。

但若將能量再細分為功和熱，封閉系統可以再多區分出二類，其性質介於封閉系統和孤立系統之間：若系統不允許外界交換熱，只能有功的交換，稱為絕熱封閉系統或熱孤立系統（英語：Thermally isolated system），若系統不允許外界交換功，只能有能的交換，稱為Adynamically封閉系統[30]，也稱作力學孤立系統。

熱力學設備

[編輯]
卡諾循環，其中的TH和TC就是高溫熱庫及低溫熱庫

熱力學設備（英語：thermodynamic instruments）可分為二種，分為是儀表（meter）和源（reservoir）。熱力學儀表是指任何可以量測熱力學系統中參數的設備。有時熱力學的參數是用理想的量測儀表來定義，例如熱力學第零定律說明若二個物體分別和一個物體達到熱平衡，這二個物體之間也達到了熱平衡。馬克士威在1872年時提出熱力學第零定律，也提到可以量測溫度的方式。理想的溫度計是在定壓下定量的理想氣體，根據理想氣體定律，氣體的體積即可用來表示壓強，雖然壓強是用力學的方式定義，也可以用定溫下定量的理想氣體的體積來當作理想的氣壓表。熱量計則是量測系統內能及能量變化的設備。

熱力學源是指一個很大的系統，和測試系統接觸時其特定狀態幾乎不會變化。熱力學源一般是用來將系統的狀態施加到某一特定數值。像壓強源是在特定壓強下的系統，和其他系統連接後，會使其他系統的壓強等於該特定值。地球的大氣常作為壓強源。熱力學中常見的熱力學源是熱庫，是特定溫度下的系統，像卡諾循環中就用到了高溫熱庫及低溫熱庫。[31]

共軛變數

[編輯]
主條目：共軛變數 (熱力學)

能量是熱力學的中心概念之一。熱力學第一定律說明系統和環境的總能量守恆。若要加入能量到系統中，可以透過加熱、壓縮、加入物質的方式。若要從系統中提出能量，則可以透過冷卻、膨脹、移出物質的方式。例如在力學的能量轉移等於對一物體的施力及物體的位移。

共軛變數是成對的熱力學概念，其中第一個表示施加在熱力學系統中的某種「力」，第二個則表示熱力學系統上的某種「位移」，二者的乘積即為轉移的能量。常見的共軛變數有：

局限性

[編輯]

熱力學由於發展較早，也有其自身的局限性，主要表現在：

  1. 它僅適用於粒子很多的巨觀系統；
  2. 它主要研究物質在平衡態下的性質，並不解答系統達到平衡態的詳細過程；
  3. 它把物質視作「連續體」，不考慮物質的微觀結構。

統計物理學與熱力學結合起來研究熱現象常常可以彌補以上局限性[32]。

子學科

[編輯]

注釋

[編輯]
  1. ^ The Newcomen engine was improved from 1711 until Watt's work, making the efficiency comparison subject to qualification, but the increase from the Newcomen 1765 version was on the order of 100%.

參考文獻

[編輯]
  1. ^ Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics. McGraw Hill. 2005. ISBN 0-07-310445-0. OCLC 56491111. 
  2. ^ Haynie, Donald, T. Biological Thermodynamics. Cambridge University Press. 2001. ISBN 0-521-79549-4. OCLC 43993556. 
  3. ^ Clausius, Rudolf. On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff's Annalen der Physik, LXXIX (Dover Reprint). 1850. ISBN 0-486-59065-8. 
  4. ^ Sir William Thomson, LL.D. D.C.L., F.R.S. Mathematical and Physical Papers 1. London, Cambridge: C.J. Clay, M.A. & Son, Cambridge University Press. 1882: 232 [2013-05-10]. （原始內容存檔於2013-06-20）. 
  5. ^ Hess, H. (1840). Thermochemische Untersuchungen （頁面存檔備份，存於網際網路檔案館）, Annalen der Physik und Chemie (Poggendorff, Leipzig) 126(6): 385–404.
  6. ^ 6.0 6.1 Enrico Fermi. Thermodynamics. Courier Dover Publications. 1956: ix. ISBN 0-486-60361-X. OCLC 230763036、54033021. 
  7. ^ Gibbs, Willard, J. (1876). Transactions of the Connecticut Academy, III, pp. 108–248, Oct. 1875 – May 1876, and pp. 343–524, May 1877 – July 1878.
  8. ^ Duhem, P.M.M. (1886). Le Potential Thermodynamique et ses Applications, Hermann, Paris.
  9. ^ Lewis, Gilbert N.; Randall, Merle. Thermodynamics and the Free Energy of Chemical Substances. McGraw-Hill Book Co. Inc. 1923. 
  10. ^ Guggenheim, E.A. (1933). Modern Thermodynamics by the Methods of J.W. Gibbs, Methuen, London.
  11. ^ Guggenheim, E.A. (1949/1967)
  12. ^ Ilya Prigogine, I. & Defay, R., translated by D.H. Everett. Chemical Thermodynamics. Longmans, Green & Co., London. Includes classical non-equilibrium thermodynamics. 1954. 
  13. ^ Perrot, Pierre. A to Z of Thermodynamics. Oxford University Press. 1998. ISBN 0-19-856552-6. OCLC 123283342、38073404. 
  14. ^ Clark, John, O.E. The Essential Dictionary of Science. Barnes & Noble Books. 2004. ISBN 0-7607-4616-8. OCLC 58732844、63473130. 
  15. ^ Reif, F. Fundamentals of Statistical and Thermal Physics. New York: McGraw-Hill Book Company. 1965: 122. 
  16. ^ Fowler, R., Guggenheim, E.A. (1939). Statistical Thermodynamics, Cambridge University Press, Canbridge UK. p. 3.
  17. ^ Bridgman, P.W. (1943). The Nature of Thermodynamics, Harvard University Press, Cambridge MA, p. 48.
  18. ^ Partington, J.R. (1949). An Advanced Treatise on Physical Chemistry, volume 1, Fundamental Principles. The Properties of Gases, Longmans, Green and Co., London. page 118.
  19. ^ Tisza, L. (1966). Generalized Thermodynamics, M.I.T Press, Cambridge MA p. 18.
  20. ^ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8. Includes local equilibrium thermodynamics.
  21. ^ Fowler, R., Guggenheim, E.A. (1939), p. 13.
  22. ^ Tisza, L. (1966), pp. 79–80.
  23. ^ Planck, M. 1923/1926, page 5.
  24. ^ Partington, p. 121.
  25. ^ Adkins, pp. 19–20.
  26. ^ Haase, R. (1971), pages 11–16.
  27. ^ Partington, J.R. A Short History of Chemistry. Dover. 1989. OCLC 19353301. 
  28. ^ Cengel, Yunus A.; Boles, Michael A. Thermodynamics – an Engineering Approach. McGraw-Hill. 2005. ISBN 0-07-310768-9. 
  29. ^ Lauth,Günter J.; Kowalczyk, Jürgen. Thermodynamik: Eine Einführung. Springer Spektrum. 2015. ISBN 978-3-662-46228-7. 
  30. ^ Partington, J.R. (1913). A Text-book of Thermodynamics, Van Nostrand, New York, page 37.
  31. ^ Windisch, Herbert. Thermodynamik: Ein Lehrbuch für Ingenieure Auflage 5. De Gruyter Oldenbourg. 2014. ISBN 978-3-486-77847-2. 
  32. ^ 秦允豪. 《热学》（第二版）. 高等教育出版社. : 第3頁. ISBN 978-7-04-013790-3. 

參見

[編輯]
取自「https://zh.wikipedia.org/w/index.php?title=热力学&oldid=82338649」