用以展示複阻抗的相量圖 。 阻抗 (英語:Electrical impedance )又稱電阻抗 [1] 電路 中電阻 、電感 、電容 對交流電 的阻礙作用的統稱。阻抗是一個複數 ,實部稱為電阻 ,虛部稱為電抗 ;其中電容在電路中對交流電所起的阻礙作用稱為容抗 ,電感在電路中對交流電所起的阻礙作用稱為感抗 ,容抗和感抗合稱為電抗 。阻抗將電阻 的概念加以延伸至交流電路領域,不僅描述電壓與電流的相對振幅 ,也描述其相對相位 。當通過電路的電流是直流電 時,電阻與阻抗相等,電阻可以視為相位為零的阻抗。阻抗的概念不僅存在於電路中,在力學的振動系統中也有涉及。
阻抗通常以符號
Z
{\displaystyle Z}
相量
Z
m
∠
θ
{\displaystyle Z_{m}\angle \theta }
Z
m
e
j
θ
{\displaystyle Z_{m}e^{j\theta }}
Z
m
{\displaystyle Z_{m}}
θ
{\displaystyle \theta }
具體而言,阻抗定義為電壓與電流的頻域 比率[2]
Z
m
{\displaystyle Z_{m}}
θ
{\displaystyle \theta }
相位差 。採用國際單位制 ,阻抗的單位是歐姆 (Ω),與電阻 的單位相同。阻抗的倒數 是導納 ,即電流與電壓的頻域 比率。導納的單位是西門子 (單位) (舊單位是姆歐 )。
英文術語「impedance」是由物理學者奧利弗·黑維塞 於1886年發表論文《電工》給出[3] [4] 電機工程師 亞瑟·肯乃利 (Arthur Kennelly )最先以複數表示阻抗[5]
1927年,孔祥鵝 《商榷電機工程譯名問題》一文建議採用「電阻抗」作為該術語中文譯名 ,以便顧及與「電抗 」(electrical reactance)、「電阻 」(electrical resistance)二詞的學理關聯[6]
阻抗是複數,可以與術語「複阻抗」替換使用。阻抗通常以相量來表示,這種表示法稱為「相量表示法」。相量有三種等價形式:
直角形式:
R
+
j
X
{\displaystyle R+jX}
極形式:
Z
m
∠
θ
{\displaystyle Z_{m}\angle \theta }
指數形式:
Z
m
e
j
θ
{\displaystyle Z_{m}e^{j\theta }}
其中,電阻
R
{\displaystyle R}
電抗
X
{\displaystyle X}
Z
m
{\displaystyle Z_{m}}
j
{\displaystyle j}
虛數單位 ,
θ
{\displaystyle \theta }
從指數形式轉換到直角形式可以使用方程式
R
=
Z
m
cos
θ
{\displaystyle R=Z_{m}\cos \theta }
X
=
Z
m
sin
θ
{\displaystyle X=Z_{m}\sin \theta }
從直角形式轉換到指數形式可以使用方程式
Z
m
=
R
2
+
X
2
{\displaystyle Z_{m}={\sqrt {R^{2}+X^{2}}}}
θ
=
arctan
(
X
/
R
)
{\displaystyle \theta =\arctan(X/R)}
極形式適用於實際工程標示,而直角形式比較適用於幾個阻抗相加或相減的案例,指數形式則比較適用於幾個阻抗相乘或相除的案例。在作電路分析時,例如在計算兩個阻抗並聯 的總阻抗時,可能會需要作幾次形式轉換。這種形式轉換必需要依照複數轉換定則 。
連接於電路的交流電源會給出電壓
v
(
t
)
{\displaystyle v(t)}
負載
Z
{\displaystyle Z}
i
(
t
)
{\displaystyle i(t)}
藉著歐姆定律,可以了解阻抗的內涵[7]
v
=
i
Z
=
i
Z
m
e
j
θ
{\displaystyle v=iZ=iZ_{m}e^{j\theta }}
阻抗大小
Z
m
{\displaystyle Z_{m}}
i
{\displaystyle i}
Z
{\displaystyle Z}
v
{\displaystyle v}
相位因子
e
j
θ
{\displaystyle e^{j\theta }}
θ
{\displaystyle \theta }
θ
T
/
2
π
{\displaystyle \theta T/2\pi }
T
{\displaystyle T}
週期 )。
就像電阻將歐姆定律延伸至交流電路領域,其它直流電路分析的結果,例如電壓分配 (voltage division )、電流分配 (current division )、戴維寧定理 、諾頓定理 等等,都可以延伸至交流電路領域,只需要將電阻更換為阻抗就行了。
電路內的廣義阻抗可以描繪為與電阻符號相同的形狀,或者描繪為加有標籤的盒子。 為了簡化計算,正弦電壓波
v
(
t
)
{\displaystyle v(t)}
i
(
t
)
{\displaystyle i(t)}
[7]
v
(
t
)
=
V
m
e
j
(
ω
t
+
ϕ
V
)
{\displaystyle v(t)=V_{m}e^{j(\omega t+\phi _{V})}}
i
(
t
)
=
I
m
e
j
(
ω
t
+
ϕ
I
)
{\displaystyle i(t)=I_{m}e^{j(\omega t+\phi _{I})}}
其中,
V
m
>
0
{\displaystyle V_{m}>0}
I
m
>
0
{\displaystyle I_{m}>0}
ω
{\displaystyle \omega }
角頻率 、
ϕ
V
{\displaystyle \phi _{V}}
ϕ
I
{\displaystyle \phi _{I}}
阻抗定義為電壓除以電流:
Z
=
d
e
f
v
(
t
)
i
(
t
)
{\displaystyle Z\ {\stackrel {def}{=}}\ {\frac {v(t)}{i(t)}}}
將這公式代入歐姆定律,可以得到
V
m
e
j
(
ω
t
+
ϕ
V
)
=
I
m
e
j
(
ω
t
+
ϕ
I
)
Z
m
e
j
θ
=
I
m
Z
m
e
j
(
ω
t
+
ϕ
I
+
θ
)
{\displaystyle {\begin{aligned}V_{m}e^{j(\omega t+\phi _{V})}&=I_{m}e^{j(\omega t+\phi _{I})}Z_{m}e^{j\theta }\\&=I_{m}Z_{m}e^{j(\omega t+\phi _{I}+\theta )}\\\end{aligned}}}
。 注意到對於任意時間
t
{\displaystyle t}
V
m
=
I
m
Z
m
{\displaystyle V_{m}=I_{m}Z_{m}}
ϕ
V
=
ϕ
I
+
θ
{\displaystyle \ \phi _{V}=\phi _{I}+\theta }
第一個方程式乃是熟悉的表達電壓與電流之間關係的歐姆定律,第二個方程式給出相位關係。
用相量表示法來描述,相量
V
{\displaystyle V}
I
{\displaystyle I}
V
=
V
m
e
j
ϕ
V
{\displaystyle V=V_{m}e^{j\phi _{V}}}
I
=
I
m
e
j
ϕ
I
{\displaystyle I=I_{m}e^{j\phi _{I}}}
正弦波
v
(
t
)
{\displaystyle v(t)}
i
(
t
)
{\displaystyle i(t)}
V
{\displaystyle V}
I
{\displaystyle I}
v
(
t
)
=
V
e
j
ω
t
{\displaystyle v(t)=Ve^{j\omega t}}
i
(
t
)
=
I
e
j
ω
t
{\displaystyle i(t)=Ie^{j\omega t}}
阻抗的定義為
Z
=
d
e
f
V
I
{\displaystyle Z\ {\stackrel {def}{=}}\ {\frac {V}{I}}}
根據歐拉公式 ,餘弦函數可以表示為
cos
(
ω
t
+
ϕ
)
=
1
2
[
e
j
(
ω
t
+
ϕ
)
+
e
−
j
(
ω
t
+
ϕ
)
]
{\displaystyle \cos(\omega t+\phi )={\frac {1}{2}}{\Big [}e^{j(\omega t+\phi )}+e^{-j(\omega t+\phi )}{\Big ]}}
這是一個可以用來表示電壓或電流波形的實值餘弦函數,可以被分解為兩個複值函數。所以,只要分析方程式右邊的兩個複值項目的行為,就可以明瞭方程式左邊的實值餘弦函數的行為。由於這兩個複值項目的實部相等,實際而言,只需要分析其中一個項目,取這項目的實部,就可以得到餘弦函數:
cos
(
ω
t
+
ϕ
)
=
R
e
{
e
j
(
ω
t
+
ϕ
)
}
{\displaystyle \cos(\omega t+\phi )=\mathrm {Re} {\Big \{}e^{j(\omega t+\phi )}{\Big \}}}
換句話說,只要取計算結果的實部,就可以得到答案。
在傅立葉分析 中,激勵可以寫成多個正弦波 的疊加。根據疊加原理 ,每個正弦波可以單獨分析計算出各自的反應,(反應本身也是一個正弦波,其頻率與激勵的頻率相同,但通常兩者的振幅 、相位 都不相同,反應的振幅、相位會有所改變。)對於原本激勵的響應是所有單獨正弦波的響應在時域的總和(或積分)。這些單獨正弦波都可以轉換為以複數運算。[8]
相量是一個常定複數,可以代表參數為時間的正弦函數的複振幅(大小和相位)。電機工程師常會使用相量作複數運算,因為能夠簡化涉及正弦函數的運算,將一個微分方程式問題約化為代數方程式問題。
一個電路元件的阻抗可以定義為元件兩端的電壓相量與通過元件的電流相量,兩者之間的比率,即電壓與電流之間的相對振幅與相對相位。注意到因子
e
j
ω
t
{\displaystyle e^{j\omega t}}
歐姆定律 給出的定義,
電容器兩端的電壓滯後於通過電容器的電流,兩者之間的相位差為
π
/
2
{\displaystyle \pi /2}
π
/
2
{\displaystyle \pi /2}
理想電阻器 的阻抗
Z
R
{\displaystyle Z_{R}}
Z
R
=
R
{\displaystyle Z_{R}=R}
其中,
R
{\displaystyle R}
理想電容器 和理想電感器 的阻抗
Z
C
{\displaystyle Z_{C}}
Z
L
{\displaystyle Z_{L}}
Z
C
=
1
j
ω
C
{\displaystyle Z_{C}={\frac {1}{j\omega C}}}
Z
L
=
j
ω
L
{\displaystyle Z_{L}=j\omega L}
其中,
C
{\displaystyle C}
電容 ,
L
{\displaystyle L}
電感 。
注意到以下兩個很有用的全等式:
j
=
e
j
π
/
2
{\displaystyle j=e^{j\pi /2}}
−
j
=
e
−
j
π
/
2
{\displaystyle -j=e^{-j\pi /2}}
應用這些全等式,理想電容器和理想電感器的阻抗以指數形式重寫為
Z
C
=
e
−
j
π
/
2
ω
C
{\displaystyle Z_{C}={\frac {e^{-j\pi /2}}{\omega C}}}
Z
L
=
ω
L
e
j
π
/
2
{\displaystyle Z_{L}=\omega Le^{j\pi /2}}
給定通過某阻抗元件的電流振幅,複阻抗的大小給出這阻抗元件兩端的電壓振幅,而複阻抗的指數因子則給出相位關係。
電阻器、電容器和電感器是三種基本電路元件。以下段落會推導出這些元件的阻抗。這些導引假定正弦信號。通過傅立葉分析 ,任意信號可以視為一組正弦函數的總和。所以,這些導引可以延伸至任意信號。
根據歐姆定律,通過電阻器的含時電流
i
R
(
t
)
{\displaystyle i_{R}(t)}
v
R
(
t
)
{\displaystyle v_{R}(t)}
v
R
(
t
)
=
i
R
(
t
)
R
{\displaystyle v_{R}(t)=i_{R}(t)R}
其中,
t
{\displaystyle t}
設定含時電壓信號為
v
R
(
t
)
=
V
0
cos
(
ω
t
)
=
V
0
e
j
ω
t
,
V
0
>
0
{\displaystyle v_{R}(t)=V_{0}\cos(\omega t)=V_{0}e^{j\omega t},\qquad V_{0}>0}
則含時電流為
i
R
(
t
)
=
V
0
R
e
j
ω
t
{\displaystyle i_{R}(t)={\frac {V_{0}}{R}}e^{j\omega t}}
兩者的大小分別為
V
0
{\displaystyle V_{0}}
V
0
/
R
{\displaystyle V_{0}/R}
ω
t
{\displaystyle \omega t}
Z
R
=
R
{\displaystyle Z_{R}=R}
電阻器的阻抗是實數。理想電阻器不會製造相位差。
通過電容器的含時電流
i
C
(
t
)
{\displaystyle i_{C}(t)}
v
C
(
t
)
{\displaystyle v_{C}(t)}
i
C
(
t
)
=
C
d
v
C
(
t
)
d
t
{\displaystyle i_{C}(t)=C{\frac {\operatorname {d} v_{C}(t)}{\operatorname {d} t}}}
設定含時電壓信號為
v
C
(
t
)
=
V
0
sin
(
ω
t
)
=
Re
{
V
0
e
j
(
ω
t
−
π
/
2
)
}
=
Re
{
V
C
e
j
ω
t
}
,
w
h
e
r
e
V
0
>
0
,
V
C
=
V
0
e
j
(
−
π
/
2
)
{\displaystyle v_{C}(t)=V_{0}\sin(\omega t)=\operatorname {Re} \{V_{0}e^{j(\omega t-\pi /2)}\}=\operatorname {Re} \{V_{C}e^{j\omega t}\},\quad where\quad V_{0}>0,\quad V_{C}=V_{0}e^{j(-\pi /2)}}
則電流為
i
C
(
t
)
=
ω
V
0
C
cos
(
ω
t
)
=
Re
{
ω
V
0
C
e
j
ω
t
}
=
Re
{
I
C
e
j
ω
t
}
{\displaystyle i_{C}(t)=\omega V_{0}C\cos(\omega t)=\operatorname {Re} \{\omega V_{0}Ce^{j\omega t}\}=\operatorname {Re} \{I_{C}e^{j\omega t}\}}
兩者的除商為
v
C
(
t
)
i
C
(
t
)
=
V
0
sin
(
ω
t
)
ω
V
0
C
cos
(
ω
t
)
=
sin
(
ω
t
)
ω
C
sin
(
ω
t
+
π
2
)
{\displaystyle {\frac {v_{C}(t)}{i_{C}(t)}}={\frac {V_{0}\sin(\omega t)}{\omega V_{0}C\cos(\omega t)}}={\frac {\sin(\omega t)}{\omega C\sin \left(\omega t+{\frac {\pi }{2}}\right)}}}
所以,電容器阻抗的大小為
1
/
ω
C
{\displaystyle 1/\omega C}
以相量 形式表示,
V
C
=
V
0
e
j
(
−
π
/
2
)
,
V
0
>
0
{\displaystyle V_{C}=V_{0}e^{j(-\pi /2)},\qquad V_{0}>0}
I
C
=
ω
V
0
C
e
j
0
{\displaystyle I_{C}=\omega V_{0}Ce^{j0}}
Z
C
=
e
−
j
π
/
2
ω
C
{\displaystyle Z_{C}={\frac {e^{-j\pi /2}}{\omega C}}}
或者,應用歐拉公式,
Z
C
=
1
j
ω
C
{\displaystyle Z_{C}={\frac {1}{j\omega C}}}
通過電感器的含時電流
i
L
(
t
)
{\displaystyle i_{L}(t)}
v
L
(
t
)
{\displaystyle v_{L}(t)}
v
L
(
t
)
=
L
d
i
L
(
t
)
d
t
{\displaystyle v_{L}(t)=L{\frac {\operatorname {d} i_{L}(t)}{\operatorname {d} t}}}
設定含時電流信號為
i
L
(
t
)
=
I
0
cos
(
ω
t
)
{\displaystyle i_{L}(t)=I_{0}\cos(\omega t)}
則電壓為
v
L
(
t
)
=
−
ω
L
I
0
sin
(
ω
t
)
=
ω
L
I
0
cos
(
ω
t
+
π
/
2
)
{\displaystyle v_{L}(t)=-\omega LI_{0}\sin(\omega t)=\omega LI_{0}\cos(\omega t+\pi /2)}
兩者的除商為
v
L
(
t
)
i
L
(
t
)
=
ω
L
cos
(
ω
t
+
π
/
2
)
cos
(
ω
t
)
{\displaystyle {\frac {v_{L}(t)}{i_{L}(t)}}={\frac {\omega L\cos(\omega t+\pi /2)}{\cos(\omega t)}}}
所以,電感器阻抗的大小為
ω
L
{\displaystyle \omega L}
以相量 形式表示,
i
L
(
t
)
=
I
0
e
j
ω
t
,
I
0
>
0
{\displaystyle i_{L}(t)=I_{0}e^{j\omega t},\qquad I_{0}>0}
v
L
(
t
)
=
ω
L
I
0
e
j
(
ω
t
+
π
/
2
)
{\displaystyle v_{L}(t)=\omega LI_{0}e^{j(\omega t+\pi /2)}}
Z
L
=
ω
L
e
j
π
/
2
{\displaystyle Z_{L}=\omega Le^{j\pi /2}}
或者,應用歐拉公式,
Z
L
=
j
ω
L
{\displaystyle Z_{L}=j\omega L}
以
j
ω
{\displaystyle j\omega }
j
ω
{\displaystyle j\omega }
s
{\displaystyle s}
時域 的信號,經過拉普拉斯變換 後,會改為表示於頻域 的信號,改成以複角頻率表示。採用這更廣義的標記,基本電路元件的阻抗為
元件
阻抗表達式
電阻器
R
{\displaystyle R}
電容器
1
/
s
C
{\displaystyle 1/sC}
電感器
s
L
{\displaystyle sL}
對於直流電路,這簡化為
s
=
0
{\displaystyle s=0}
s
=
j
ω
{\displaystyle s=j\omega }
電抗是阻抗的虛部。電阻
R
{\displaystyle R}
X
{\displaystyle X}
Z
m
=
Z
Z
∗
=
R
2
+
X
2
{\displaystyle Z_{m}={\sqrt {ZZ^{*}}}={\sqrt {R^{2}+X^{2}}}}
θ
=
arctan
(
X
R
)
{\displaystyle \theta =\arctan {\left({\frac {X}{R}}\right)}}
具有有限電抗的電路元件,會使得其兩端的電壓與通過的電流發生相位差
θ
{\displaystyle \theta }
X
=
Z
m
sin
θ
{\displaystyle X=Z_{m}\sin \theta }
運作時,純電抗元件會交替地從電路吸收電能,然後又將電能還給電路;純電抗元件不會耗散任何電能。
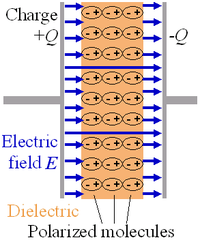
電介質分子因為電子受到電場影響,使得分子偏離平衡位置。為了方便說明,本圖將電介質和電極的空隙加大,實際上電介質會直接和電極接觸。 理想電容器 的阻抗是虛數,不具有實部,其虛部稱為「容抗」,與信號的角頻率成反比。電容器是由兩塊導體 和夾在中間的電介質 構成,其容抗為
X
C
=
−
j
/
ω
C
{\displaystyle X_{C}=-j/\omega C}
從這方程式可以觀察到,當交流電源的角頻率
ω
{\displaystyle \omega }
斷路 。假設電源的頻率越高,則容抗越低,對於電流通過的阻礙也越低。在高頻率運作時,電容器貌似短路 。
更詳細地描述,假設連接直流電流源於平行板電容器 的兩端,由於電容器中有絕緣的電介質阻隔,電荷無法穿過電容器,電容器的一塊平行板會累積正電荷,另一塊平行板會累積負電荷。這過程稱為「充電」。注意到在這充電過程,整個電容器仍舊維持電中性。分別累積於兩塊平行板的正電荷和負電荷會產生電場。依照不同的電介質屬性而定,這電場會將電介質的正負電荷稍微分開,或者按照電場方向改變每一個電介質分子的定向,將電介質電極化 ,這會在電介質的表面形成面束縛電荷 與其對應的感應電場,其方向與原本電場相反,因此減弱原本電場的實際作用,所以電介質可以增加電容器的電容。由於電容器的總電場,電容器的兩塊平行板之間會出現電壓。等到這電壓不再變動之後,通過電容器的電流會等於零,所以,一般會說電容器不允許直流電流通過。
假設連接交流電流源或交流電壓源於平行板電容器的兩端,由於電流會週期性的變換方向,交流電流會輪流對電容器的兩塊平行板充電和放電,處於兩塊平行板的電荷會週期性的變化,因此在一個週期內,除了電流由正變負(或由負變正)的那一瞬間之外,通過電容器的電流均不為零。因此,一般認為電容器可允許交流電流通過。注意到電容器只能夠累積有限量的電荷。
理想電感器 的阻抗是虛數,不具有實部,其虛部稱為「感抗」,與信號的角頻率成正比:
X
L
=
ω
L
j
{\displaystyle X_{L}=\omega Lj}
其中,
X
L
{\displaystyle X_{L}}
從這方程式可以觀察到,當交流電源的角頻率趨向於零時,電源會趨向於直流電源,感抗會趨向於零,對於電流的通過阻礙越低。所以,在低頻率運作時,電感器貌似短路 。假設電源角頻率越高,則感抗越高,假設給定電壓源振幅,則電流會趨向於零。所以,在高頻率運作時,電感器貌似斷路 。
電感器是一個線圈導體。根據法拉第感應定律 ,通過載流迴圈的磁通量 變率,會生成的感應電動勢 為
E
=
−
d
Φ
B
d
t
{\displaystyle {\mathcal {E}}=-{{\operatorname {d} \Phi _{B}} \over \operatorname {d} t}}
其中,
E
{\displaystyle {\mathcal {E}}}
Φ
B
{\displaystyle \Phi _{B}}
假設電感器的線圈匝數是
N
{\displaystyle N}
E
=
−
N
d
Φ
B
d
t
{\displaystyle {\mathcal {E}}=-N{\operatorname {d} \Phi _{B} \over \operatorname {d} t}}
感應電動勢會阻礙電流流動。常定直流電所產生的磁場,其通過線圈的磁通量是個常數,變率為零,感應電動勢也為零。所以,常定直流電會將電感器視為短路(通常電感器的材質為低電阻率材料)。交流電變率的時間平均值跟頻率成正比,因此感抗與頻率也成正比。
應用串聯電路和並聯電路的阻抗計算定則,就可以計算出簡單電路的總阻抗。除了阻抗是複數以外,這定則與串聯電路和並聯電路的電阻計算定則等同。但是,對於一般電路案例,還需要通過等效阻抗轉換 (equivalent impedance transform )這一道步驟。
星形電路 和三角形電路 示意圖。具有多於兩個終端點的阻抗電路,無法約化為只具有一個阻抗元件的等效電路;具有
n
{\displaystyle n}
n
>
2
{\displaystyle n>2}
n
{\displaystyle n}
三角形電路 或具有四個節點的星形電路 。這兩種等價電路可以互相變換。具有任意個終端點的一般電路,只靠串聯和並聯組和,無法約化為具有最少個阻抗元件的電路(稱為「最少電路」);通常,還必需使用角星變換 和星角變換 。理論上,可以證明這些變換足夠找到最少電路;不須要任何其他種複雜變換。
以串聯方式相連接的元件。 假設一個電路的元件是以串聯方式相連接,則通過每一個元件的電流都相等,等效阻抗是每一個元件的阻抗的總和:
Z
e
q
=
d
e
f
Z
1
+
Z
2
+
⋯
+
Z
n
{\displaystyle Z_{eq}\ {\stackrel {def}{=}}\ Z_{1}+Z_{2}+\cdots +Z_{n}}
其中,
Z
e
q
{\displaystyle Z_{eq}}
Z
i
{\displaystyle Z_{i}}
i
{\displaystyle i}
以實部項目和虛部項目表示,
Z
e
q
=
R
e
q
+
j
X
e
q
=
(
R
1
+
R
2
+
⋯
+
R
n
)
+
j
(
X
1
+
X
2
+
⋯
+
X
n
)
{\displaystyle Z_{eq}=R_{eq}+jX_{eq}=(R_{1}+R_{2}+\cdots +R_{n})+j(X_{1}+X_{2}+\cdots +X_{n})}
以並聯方式相連接的元件。 假設一個電路的元件是以並聯方式相連接,則每一個元件兩端的電壓都相等,每一個元件的阻抗的倒數,總和起來就是等效阻抗的倒數:
1
Z
e
q
=
d
e
f
1
Z
1
+
1
Z
2
+
⋯
+
1
Z
n
{\displaystyle {\frac {1}{Z_{eq}}}\ {\stackrel {def}{=}}\ {\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}+\cdots +{\frac {1}{Z_{n}}}}
對於
n
=
2
{\displaystyle n=2}
Z
e
q
=
Z
1
Z
2
Z
1
+
Z
2
{\displaystyle Z_{eq}={\frac {Z_{1}Z_{2}}{Z_{1}+Z_{2}}}}
以實部項目
R
e
q
{\displaystyle R_{eq}}
X
e
q
{\displaystyle X_{eq}}
Z
e
q
=
R
e
q
+
j
X
e
q
{\displaystyle Z_{eq}=R_{eq}+jX_{eq}}
其中,
R
e
q
=
(
X
1
R
2
+
X
2
R
1
)
(
X
1
+
X
2
)
+
(
R
1
R
2
−
X
1
X
2
)
(
R
1
+
R
2
)
(
R
1
+
R
2
)
2
+
(
X
1
+
X
2
)
2
{\displaystyle R_{eq}={\frac {(X_{1}R_{2}+X_{2}R_{1})(X_{1}+X_{2})+(R_{1}R_{2}-X_{1}X_{2})(R_{1}+R_{2})}{(R_{1}+R_{2})^{2}+(X_{1}+X_{2})^{2}}}}
X
e
q
=
(
X
1
R
2
+
X
2
R
1
)
(
R
1
+
R
2
)
−
(
R
1
R
2
−
X
1
X
2
)
(
X
1
+
X
2
)
(
R
1
+
R
2
)
2
+
(
X
1
+
X
2
)
2
{\displaystyle X_{eq}={\frac {(X_{1}R_{2}+X_{2}R_{1})(R_{1}+R_{2})-(R_{1}R_{2}-X_{1}X_{2})(X_{1}+X_{2})}{(R_{1}+R_{2})^{2}+(X_{1}+X_{2})^{2}}}}
當測量電路元件的阻抗時,必需先了解測量值與真實值之間可能會出現的差別。這是因為測量儀器本身的殘餘阻抗和測量的準確度問題。給定已知阻抗真實值的元件,然後比較其測量值與真實值,就可以知道這測量方法的優劣。
測量阻抗的方法有很多種,例如,電橋法、諧振法、電壓-電流法、阻抗頻譜法等等[9] [10]
交流電橋電路圖 交流電橋貌似惠斯登橋 ,可以用來測量阻抗。將交流電源連接於交流電橋兩端,電橋的四個元件的阻抗分別為
Z
1
{\displaystyle Z_{1}}
Z
2
{\displaystyle Z_{2}}
Z
3
{\displaystyle Z_{3}}
Z
x
{\displaystyle Z_{x}}
Z
x
=
Z
2
Z
3
/
Z
1
{\displaystyle Z_{x}=Z_{2}Z_{3}/Z_{1}}
以相量表示,
Z
x
=
|
Z
x
|
∠
θ
x
=
|
Z
2
Z
3
/
Z
1
|
∠
(
θ
2
+
θ
3
−
θ
1
)
{\displaystyle Z_{x}=|Z_{x}|\angle \theta _{x}=|Z_{2}Z_{3}/Z_{1}|\angle (\theta _{2}+\theta _{3}-\theta _{1})}
這方法歷史悠久,很容易製作成品儀器,費用低廉,準確率高;但是,不能夠自動化,必需手工調整已知阻抗來達成平衡,而且電橋的測量頻域比較狹窄。
諧振法電路圖 諧振法依賴RLC串聯電路 在共振 狀況的物理行為來測量元件的阻抗。這方法使用到品質因子 (Q factor )
Q
{\displaystyle Q}
測Q計 (Q meter )測量一電路元件所得到的
Q
{\displaystyle Q}
[10]
施加正弦電壓源於電路。設定測試的頻率為
ω
{\displaystyle \omega }
調整可調電容器的電容
C
{\displaystyle C}
Q
{\displaystyle Q}
如右圖所示,將阻抗為
Z
x
{\displaystyle Z_{x}}
C
′
{\displaystyle C'}
Q
′
{\displaystyle Q'}
對於第一個共振狀況,可調電容器的電抗
X
C
{\displaystyle X_{C}}
X
L
{\displaystyle X_{L}}
X
C
+
X
L
=
0
{\displaystyle X_{C}+X_{L}=0}
所以,
1
ω
C
=
ω
L
{\displaystyle {\frac {1}{\omega C}}=\omega L}
從前面關於品質因子的論述,可以寫出
Q
=
|
X
C
|
R
=
1
ω
C
R
=
ω
L
R
{\displaystyle Q={\frac {|X_{C}|}{R}}={\frac {1}{\omega CR}}={\frac {\omega L}{R}}}
對於第二個共振狀況,被測元件的電抗
X
X
{\displaystyle X_{X}}
X
C
′
+
X
X
+
X
L
=
0
{\displaystyle X_{C'}+X_{X}+X_{L}=0}
所以,被測元件的電抗為
X
X
=
1
ω
C
′
−
ω
L
=
1
ω
C
′
−
1
ω
C
=
C
−
C
′
ω
C
C
′
{\displaystyle X_{X}={\frac {1}{\omega C'}}-\omega L={\frac {1}{\omega C'}}-{\frac {1}{\omega C}}={\frac {C-C'}{\omega CC'}}}
品質因子為
Q
′
=
|
X
C
′
|
R
X
+
R
=
1
ω
C
′
(
R
X
+
R
)
{\displaystyle Q'={\frac {|X_{C'}|}{R_{X}+R}}={\frac {1}{\omega C'(R_{X}+R)}}}
所以,被測元件的電阻為
R
X
=
1
ω
C
′
Q
′
−
1
ω
C
Q
{\displaystyle R_{X}={\frac {1}{\omega C'Q'}}-{\frac {1}{\omega CQ}}}
被測元件的阻抗為
Z
X
=
R
X
+
j
X
X
=
(
1
ω
C
′
Q
′
−
1
ω
C
Q
)
+
j
(
1
ω
C
′
−
1
ω
C
)
{\displaystyle Z_{X}=R_{X}+jX_{X}=\left({\frac {1}{\omega C'Q'}}-{\frac {1}{\omega CQ}}\right)+j\left({\frac {1}{\omega C'}}-{\frac {1}{\omega C}}\right)}
這方法可以用於測量高品質因子的元件。但是,必需手工調整來達成共振。
^ 存档副本 . [2021-09-21 ] . (原始內容 存檔於2021-09-21). ^ Alexander, Charles; Sadiku, Matthew, Fundamentals of Electric Circuits 3, revised, McGraw-Hill: pp. 387–389, 2006, ISBN 9780073301150 ^ Science , p. 18, 1888^ Oliver Heaviside, The Electrician , p. 212, 23rd July 1886 reprinted as Electrical Papers , p64, AMS Bookstore, ISBN 978-0-8218-3465-7
^ Katz, Eugenii, 對於電磁學有巨大貢獻的著名科學家:亞瑟·肯乃利 , (原始內容 存檔於2009-10-27) ^ 存档副本 . [2019-12-14 ] . (原始內容存檔 於2019-05-12). ^ 7.0 7.1 Horowitz, Paul; Hill, Winfield. 1. The Art of Electronics . Cambridge University Press. 1989: 31 –33. ISBN 0-521-37095-7 ^ Alexander, Charles; Sadiku, Matthew, Fundamentals of Electric Circuits 3, revised, McGraw-Hill: pp. 829–830, 2006, ISBN 9780073301150 ^ Agilent Impedance Measurement Handbook (PDF) 4th, USA: Agilent Technologies: pp.22ff, 2009, (原始內容 (PDF) 存檔於2011-05-16) ^ 10.0 10.1 Bakshi, V. U.; Bakshi, U. A., Electronic Measurements, Technical Publications: pp. 68ff, 110ff, 2007, ISBN 9788189411756


















































![{\displaystyle \cos(\omega t+\phi )={\frac {1}{2}}{\Big [}e^{j(\omega t+\phi )}+e^{-j(\omega t+\phi )}{\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe179761c6d8bd429e70771c89e19bccb20e42b)


























































































