月球軌道
| ||||||||||||||||||||||||||||||||
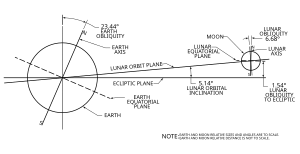
| 月球相對於地球的軌道圖。雖然角度和 相對大小是依比例繪製,但距離不是。 | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
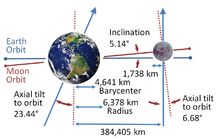
月球軌道 以順行的方向繞行地球,相對於春分點和恆星完成一個公轉大約是27.32天(分點月和恆星月),相對於太陽的一次公轉約29.53天(朔望月)。地球和月球圍繞其重心(公共質量中心)軌道運行,距離地球中心約4,670 km(2,900 mi)(約其半徑的73%),形成一個衛星系統,稱為地月系統。平均而言,地球到月球的距離距離地球中心約385,000 km(239,000 mi),相當於約60個地球半徑或1.282光秒。
平均軌道速度為1.022公里/秒(0.635英里/秒)[9],月球每小時在天球上大約覆蓋其直徑的距離,或大約半度。月球不同於其他行星的大多數衛星,因為它的軌道靠近黃道平面,而不是其主星(在這種情況下,是地球)的赤道平面。月球的軌道面相對於黃道面傾斜約為5.1°,而月球的赤道面傾斜僅為1.5°。
性質
[編輯]本節中描述的軌道特性是近似值。由於太陽和行星的重力作用,月球繞地球的軌道有許多變化(攝動),對此研究(月球理論)已有著悠久的歷史[10]。
橢圓形狀
[編輯]月球繞地球的軌道是一個近乎圓形的橢圓(半長軸和半短軸分別為384,400km和383,800km:相差僅0.16%)。橢圓方程式產生的 近地點和遠地點的平均距離分別為362,600公里和405,400公里(相差12%),
由於較近的物體看起來更大,月球的表觀大小會隨著它靠近或遠離地球上的觀察者而變化。當滿月離地球最近(近地點)時,此時的滿月被稱為「超級月亮」。月球可能的最大視直徑(近地點與遠地點距離)比最小的直徑大14%; 表觀面積新增了30%,向地球反射的光也新增了30%。
正如克卜勒第二定律所述,月球軌道距離的變化與其切向速度和角速度的變化相對應。相對於地月重心處的假想觀察者的平均角運動每天向東(J2000.0曆元)13.176。
離日度
[編輯]月球的離日度是其在任何時候都位於太陽以東的角距離。朔時的月球離日度為零,即當月球處於合的月相。在滿月時,離日度為180°,即月球處於衝的月相。在這兩種情況下,月球處於朔或望的狀態,也就是說,太陽、月球和地球幾乎對齊。當離日度是90°或270°,月球的月相是方照。
進動
[編輯]
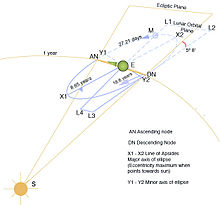
軌道的方向在空間中不是固定的,而是隨時間旋轉的。這種軌道進動稱為拱線進動,是月球軌道在軌道平面內的旋轉,即橢圓的軸改變方向。月球軌道的長軸——軌道的最長直徑,將其最近點和最遠點近地點和遠地點分別連接在一起,每8.85地球年或3,232.6054天進行一次完整的旋轉,因為它沿著與月球自身相同的方向緩慢旋轉(直接運動)——這意味著向東進動360°。月球的拱線進動不同於其軌道平面的交點進動和月球本身的軸向進動。
傾角
[編輯]月球軌道對黃道面的平均傾角為5.145°。理論上的考慮表明,現時相對於黃道面的傾角是由從早期近地軌道的潮汐演化而來,相對地球赤道的傾角相當恆定[11]。這將需要早期軌道與赤道的傾角約為10°,才能產生當前與黃道約5°的傾角。據認為,最初赤道的傾斜度接近於零,但由於微行星在墜落到地球時經過月球附近的影響,可以增加到10°[12]。如果沒有發生這種情況,月球現在將更靠近黃道,日月食將更加頻繁[13]。
月球的自轉軸不垂直於其軌道平面,因此月球赤道不在其軌道平面內,而是向其傾斜6.688°(這是轉軸傾角)。正如雅克·卡西尼(Jacques Cassini)於1722年發現的那樣,月球的自轉軸以與其軌道平面相同的速度進動,但其相位相差180°(見卡西尼定律)。因此,即使月球的自轉軸相對於恆星不是固定的,黃道和月球赤道之間的角度始終為1.543°[14]。
交點
[編輯]交點是月球軌道穿過黃道的點。月球每27.2122天穿過同一交點,這個間隔稱為"交點月"。交點線是兩個平面各自兩個交點的連結線,它是逆行的:對於地球上的觀察者來說,它沿黃道向西旋轉,週期為18.6年或每年19.3549°。當從天北方向看時,交點圍繞地球順時針移動,與地球自轉和繞太陽公轉方向相反。當交點與太陽對齊時,大約每173.3天就會發生一次月食或日食。月球軌道傾角也決定了食是否發生;當交點與滿月和新月重合時,即當太陽、地球和月球在三維中對齊時,陰影會交叉。
實際上,這意味著月球上的回歸年長度只有347天。這被稱為龍之年或食年。月球上的「季節」適合這個時期。在龍之年的大約一半時間裏,太陽位於月球赤道以北(但最大為1.543°),而另一半時間則位於月球赤道以南。顯然,與月球夜晚和白天的差異相比,這些季節的影響很小。在月球兩極,太陽將"升起"173天,而不是通常的15地球日左右的月球晝夜;極地日出和日落每次需要18地球日。這裡的"向上"表示太陽的中心在地平線之上[15]。月球極地日出和日落發生在食(日食或月食)前後。例如,在2016年3月9日日食上,月亮靠近其降交點,太陽靠近天空中月球赤道穿過黃道的點。當太陽到達該點時,太陽的中心在月球北極落下,在月球南極升起。
在同年9月1日日食中,月球靠近其升交點,太陽在天空中也靠近月球赤道穿過黃道的點。當太陽到達該點時,太陽的中心從月球北極升起,在月球南極落下。
赤道傾斜和月球至點
[編輯]每隔18.6年,月球軌道與地球赤道之間的夾角達到最大值28°36′,地球赤道傾斜(23°27′)和月球軌道傾角與黃道之間的夾角(5°09′)之和。這被稱為"最大月球至點″。大約在這個時候,月球的赤緯將從−28°36′ 到+28°36′不等。相對的,9.3年後,月球軌道與地球赤道之間的夾角達到了18°20′的最小值。這被稱為"最小月球至點"。上一次的最小月球至點發生在2015年10月。當時,降交點與春分點(天球赤道座標上赤經零和赤緯零的點)對齊。這些交點每年向西移動約19°,因此太陽每年提前20天穿過同一個給定的交點。
當月球軌道與地球赤道的傾角為最小的18°20′時,每天從低於北緯或南緯70°43′(90°-18°20′ – 57′視差)的緯度開始,月球圓盤的中心將位於地平線上方。當傾角達到最大值28°36′時,只有在緯度小於北緯或南緯60°27′(90°-28°36′–57′)的地方,月球圓盤的中心每天都會高於地平線,也就是說月球每天都會在地平線出與沒。
在高緯度地區,每月至少有一天月亮不升起,但每月至少也有一天月亮不落下。這與太陽的季節行為相似,但週期為27.2天,而不是365天。需要注意的是,由於大氣折射,當月球上的一點位於地平線以下約34弧分前時,實際上仍然可以看到該點。
由於月球軌道相對於地球赤道的傾角,即使太陽地平線以下六個月的時候,月球每月也會在北極和南極的地平線上停留大約近兩週。從月球生起到下一次再升起的週期是一個回歸月,大約是27.3天,非常接近恆星週期。當太陽離地平線最遠時(冬至),月球在其最高點時將是滿月。當月球在雙子座時,它將在北極的地平線之上,而當月球在人馬座時,它將出現在南極的地平線上。
當太陽在地平線以下數月時,北極的浮游動物會利用月球的光[16],當氣候變暖時,這對生活在北極和南極地區的動物肯定是有幫助的。
比例模型
[編輯]-
地球-月球系統的比例模型:大小和距離按比例。 它表示軌道的平均距離和兩個天體的平均半徑。
觀察和量測歷史
[編輯]
大約在西元前1000年,巴比倫人是已知的第一個對月球觀測,且持續進行記錄的人類文明。在現今的伊拉克領土上發現這一時期刻有楔形文字的粘土碑上,記錄了月球升起和落下的日期和時間,月球經過的恆星,以及滿月前後太陽和月亮升起和落下的時間差。巴比倫天文學發現了月球運動的三個主要時期,並利用數據分析建立了延續到未來的陰曆[10]。這種利用詳細、系統的觀察來根據實驗數據進行預測的方法可以被歸類為人類歷史上第一種科學研究。然而,巴比倫人似乎對他們的數據缺乏任何幾何或物理解釋,他們無法預測未來的月食(儘管在可能發生月食的時間之前會發出"警告")。
古希臘天文學家是第一個介紹和分析天體運動數學模型的人。托勒密使用定義明確的本輪和出差的幾何模型描述了月球運動[10]
以撒·牛頓爵士是第一個發展出完整運動力學理論的人。對月球運動的觀測是對他的理論的主要檢驗[10]。
月球週期
[編輯]| 名稱 | 長度(天) | 釋義 |
|---|---|---|
| 恆星月 | 27.321662 | 相對於遙遠的恆星(每個太陽軌道13.36874634月) |
| 朔望月 | 29.530589 | 相對於太陽(月相,每個太陽軌道12.36874634月) |
| 回歸月 | 27.321582 | 相對於春分點(受到約26,000年內的歲差影響) |
| 近點月 | 27.554550 | 相對於近地點 (在3232.6054天內的進動=8.850578年) |
| 交點月 | 27.212221 | 相對於升交點(進動週期6793.4765天=18.5996年) |
月球軌道有幾個不同的週期[17]。恆星月是相對於固定恆星繞地球運行一個完整軌道所需的時間,它大約是27.32天。朔望是月球達到相同視覺階段所需的時間。它在一年中變化很大[18],但平均約為29.53天。朔望週期比恆星週期長,因為地球-月球系統在每個恆星月圍繞太陽的軌道運行,因此需要更長的週期來實現地球、太陽和月球的相對位置。近點月是從近地點再回到近地點的時間,約為27.55天。地月距離決定了月球引潮力的強度。
交點月是從升交點再回升交點的時間。兩次連續經過相同黃道經度的之間的時間稱為回歸月;後一個時期與恆星月略有不同。
日曆月(一年的十二分之一)的平均長度約為30.4天。儘管曆日曆月在歷史上與可見的農曆相關,但這不是任何一種陰曆月或月相的週期。

月相:0 (1)—新月,0.25:上弦,0.5—滿月, 0.75:下弦。
潮汐演化
[編輯]月球對地球施加的重力是海洋和固體地球發生潮汐的原因;太陽對潮汐的影響較小。固體地球對潮汐力的任何變化都會做出快速反應,這種變形呈橢球狀,高點大致位於月球下方,與位於地球的另一側。這是固體地球內高速地震波的結果。
然而,地震波的速度不是無限的,再加上地球內部能量損失的影響,這會導致月球產生的最大作用力通過,和最大地球潮汐之間的輕微延遲。由於地球自轉的速度比月球繞其軌道運行的速度快,這個小角度產生的重力矩使地球減速,並使月球在其軌道上加速。
就海洋潮汐而言,潮汐波在海洋中的速度[19]遠低於月球潮汐力的速度。其結果是,海洋從未與潮汐力處於近乎平衡的狀態。相反的,這種力無論是在深海還是在淺層大陸架上,會產生長長的海浪,這些海浪在海洋盆地周圍傳播,直到最終通過亂流失去能量。
雖然海洋的回應在兩者中更為複雜,但可以將海洋潮汐分解為一個影響月球的小橢球體項,加上一個沒有影響的二次項。海洋的橢球項也減慢了地球的速度,並加速了月球的速度,但由於海洋耗散了如此多的潮汐能,因此現時的海洋潮汐影響比固體地球潮汐大一個數量級。
由於橢球體引起的潮汐扭矩,地球的一些角(或旋轉)動量正逐漸轉移到地月對圍繞其相互質心(稱為重心)的旋轉中。有關的更詳細說明,請參見潮汐加速。
這種稍大的軌道角動量導致地月距離以每年約38毫米的速度增加[20]。角動量守恆意味著地球的軸向旋轉正在逐漸減慢,因此它的一天每年延長約24微秒(不包括冰川後反彈#效應)。這兩個數值僅對各大洲的當前配置有效。來自6.2億年前韻律岩的潮汐節奏表明,在數億年的時間裡月球以每年22 mm(0.87英寸)和平均每年12微秒(或每億年20分鐘)的平均速度延長;兩者都大約是當前值的一半。
現時的高頻率可能是由於自然海洋頻率和潮汐頻率之間接近共振[21]。另一種解釋是,在過去,地球的自轉速度要快得多,在早期的地球上,一天可能只有9個小時。海洋中產生的潮汐波將短得多,並且長波長潮汐力激發短波長潮汐將更加困難[22]。
月球正在逐漸從地球退縮到更高的軌道上,計算表明這將持續約500億年[23][24]。到那時,地球和月球將處於相互旋轉軌道共振或潮汐鎖定,其中月球將在大約47天(目前為27天)內繞地球運行,月球和地球將同時圍繞其軸旋轉,始終以相同的一側面對面。這已經發生在月球上:同一側總是面向地球,並且也正慢慢地發生在地球上。然而,地球自轉的減速發生得還不夠快,以至於自轉時間在其它效應改變情況之前延長到一個月:大約23億年後,太陽輻射的增加將導致地球的海洋蒸發[25],去除大部分潮汐摩擦和加速度。
天平動
[編輯]
月球處於同步自轉,這意味著它始終保持以相同的一面朝向地球。但這種同步自轉只是平均而言正確,因為月球的軌道具有明顯的偏心率。結果是,月球的角速度隨著它繞地球運行而變化,但自轉是恆定的,因此角速度並不總是與月球的自轉速度同步。當月球處於近地點時,它的軌道運動比它的自轉快。這時,月球相對於其軸線的旋轉,在其軌道上有點領先,這產生了一種透視效果,使我們能夠看到它東側(右)背面八度的經度。相反,當月球到達其遠地點時,它的軌道運動比它的自轉慢,顯示出其西側(左)背面八度的經度。這被稱為「經度天平動」。
月球的自轉軸相對於黃道平面的法線傾角總共傾斜6.7°。這導致南北方向的類似透視效應,稱為「緯度天平動」,它允許人們看到極點以外近7°緯度的背面。最後,由於月球距離地球質心只有大約60個地球半徑,一個在赤道觀察月球的觀察者整夜觀察月球,橫向移動一個地球直徑。這產生了「周日天平動」,它允許人們查看額外的一度月球經度。出於同樣的原因,在地球的兩個地理極點的觀察者將能夠在緯度上看到額外的一度緯度天平動。
除了這些由地球上觀察者視角變化引起的「天平動」之外,還有「物理天平動」,它們是月球在太空中旋轉的極點方向實際地擺動:章動,但這個量非常小。
地球和月球圍繞太陽的路徑
[編輯]

當從北天極(即從恆星北極星的大致方向)觀察時,月球逆時針繞地球運行,地球逆時針繞太陽公轉,月球和地球自轉軸的方向也是逆時針旋轉。
右手定則可用於指示角速度的方向。如果右手的拇指指向北天極,它的手指就會向月球繞地球運行的方向捲曲,地球圍繞太陽運行,月球和地球在自己的軸上旋轉。
在太陽系的表示中,通常從太陽的角度繪製地球的軌跡,從地球的角度繪製月球的軌跡。這可能會給人一種印象,即月球繞地球運行的方式有時從太陽的角度來看會倒退。然而,由於月球繞地球的軌道速度(1km/s)與地球圍繞太陽的軌道速度(30km/s)相比很小,所以這永遠不會發生。月球在繞太陽的軌道上沒有向後的迴圈。
考慮到地月系統作為雙行星,但它的質心在地球內,距離地心大約4,671 km(2,902 mi)[27],或地球半徑73.3%之處。當地球完成其晝夜自轉時,這個質心仍然在地球和月球中心聯線的地球內。地月系統在太陽軌道上的路徑被定義為這個質心圍繞太陽的運動。因此,在每個朔望月中,因為月球圍繞共同的重心在其軌道上移動,地球的中心在太陽軌道路徑內外變動[28]。
太陽對月球的重力效應是地球對月球的兩倍多。因此,月球的軌跡總是凸的[28][29](從地月太陽軌道外的很遠距離看太陽-地-月系統時所看到的),並且沒有凹陷(從相同的角度)或迴圈[26][28]。也就是說,月球太陽軌道所包圍的區域是凸集。
相關條目
[編輯]參考資料
[編輯]- ^ The geometric mean distance in the orbit (of ELP) which is the semimajor axis of the Moon's elliptical orbit via Kepler's laws
- ^ M. Chapront-Touzé; J. Chapront. The lunar ephemeris ELP-2000. Astronomy & Astrophysics. 1983, 124: 54. Bibcode:1983A&A...124...50C.
- ^ The constant in the ELP expressions for the distance, which is the mean distance averaged over time
- ^ M. Chapront-Touzé; J. Chapront. ELP2000-85: a semi-analytical lunar ephemeris adequate for historical times. Astronomy & Astrophysics. 1988, 190: 351. Bibcode:1988A&A...190..342C.
- ^ 5.0 5.1 5.2 Meeus, Jean, Mathematical Astronomy Morsels, Richmond, VA: Willmann-Bell: 11–12, 22–23, 1997, ISBN 0-943396-51-4
- ^ Seidelmann, P. Kenneth (編), Explanatory Supplement to the Astronomical Almanac, University Science Books: 696, 701, 1992, ISBN 0-935702-68-7。
- ^ 反正弦視差ɑ/sin π傳統上是月球中心到地球中心的平均距離,此處的α是地球的赤道半徑,和 π是月亮在「α」兩端之間的視差[5]。1976年國際天文學聯合會的天文常數中有三個是「月球與地球的平均距離」384400 公里,"在平均距離的赤道水平視差" 3422.608″,和"地球赤道半徑" 6,378.14 公里[6]
- ^ Lang, Kenneth R. (2011), The Cambridge Guide to the Solar System (頁面存檔備份,存於網際網路檔案館), 2nd ed., Cambridge University Press.
- ^ Moon Fact Sheet. NASA. [2014-01-08]. (原始內容存檔於2008-12-16).
- ^ 10.0 10.1 10.2 10.3 Martin C. Gutzwiller. Moon-Earth-Sun: The oldest three-body problem. Reviews of Modern Physics. 1998, 70 (2): 589–639. Bibcode:1998RvMP...70..589G. doi:10.1103/RevModPhys.70.589.
- ^ Peter Goldreich. History of the Lunar Orbit. Reviews of Geophysics. Nov 1966, 4 (4): 411. Bibcode:1966RvGSP...4..411G. doi:10.1029/RG004i004p00411. Jihad Touma & Jack Wisdom. Evolution of the Earth-Moon system. The Astronomical Journal. Nov 1994, 108: 1943. Bibcode:1994AJ....108.1943T. doi:10.1086/117209.
- ^ Kaveh Pahlevan & Alessandro Morbidelli. Collisionless encounters and the origin of the lunar inclination. Nature. Nov 26, 2015, 527 (7579): 492–494. Bibcode:2015Natur.527..492P. PMID 26607544. S2CID 4456736. arXiv:1603.06515
 . doi:10.1038/nature16137.
. doi:10.1038/nature16137.
- ^ Jacob Aron. Flying gold knocked the moon off course and ruined eclipses. New Scientist. Nov 28, 2015 [2022-07-03]. (原始內容存檔於2022-09-30).
- ^ View of the Moon. U. of Arkansas at Little Rock. [May 9, 2016]. (原始內容存檔於2022-06-23).
- ^ Calculated from arcsin(0.25°/1.543°)/90° times 173 days, since the angular radius of the Sun is about 0.25°.
- ^ Moonlight helps plankton escape predators during Arctic winters. New Scientist. Jan 16, 2016 [2022-07-03]. (原始內容存檔於2016-01-30).
- ^ The periods are calculated from orbital elements, using the rate of change of quantities at the instant J2000. The J2000 rate of change equals the coefficient of the first-degree term of VSOP polynomials. In the original VSOP87 elements, the units are arcseconds(」) and Julian centuries. There are 1,296,000」 in a circle, 36525 days in a Julian century. The sidereal month is the time of a revolution of longitude λ with respect to the fixed J2000 equinox. VSOP87 gives 1732559343.7306」 or 1336.8513455 revolutions in 36525 days–27.321661547 days per revolution. The tropical month is similar, but the longitude for the equinox of date is used. For the anomalistic year, the mean anomaly (λ-ω) is used (equinox does not matter). For the draconic month, (λ-Ω) is used. For the synodic month, the sidereal period of the mean Sun (or Earth) and the Moon. The period would be 1/(1/m-1/e). VSOP elements from Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. Numerical expressions for precession formulae and mean elements for the Moon and planets. Astronomy and Astrophysics. February 1994, 282 (2): 669. Bibcode:1994A&A...282..663S.
- ^ Jean Meeus, Astronomical Algorithms (Richmond, VA: Willmann-Bell, 1998) p 354. From 1900–2100, the shortest time from one new moon to the next is 29 days, 6 hours, and 35 min, and the longest 29 days, 19 hours, and 55 min.
- ^ J.B. Zirkir. The Science of Ocean Waves. Johns Hopkins University Press. 2013: 264. ISBN 9781421410784.
- ^ Williams, James G.; Boggs, Dale H. Secular tidal changes in lunar orbit and Earth rotation. Celestial Mechanics and Dynamical Astronomy. 2016, 126 (1): 89–129. Bibcode:2016CeMDA.126...89W. ISSN 0923-2958. S2CID 124256137. doi:10.1007/s10569-016-9702-3 (英語).
- ^ Williams, George E. Geological constraints on the Precambrian history of Earth's rotation and the Moon's orbit. Reviews of Geophysics. 2000, 38 (1): 37–60. Bibcode:2000RvGeo..38...37W. doi:10.1029/1999RG900016.
- ^ Webb, David J. Tides and the evolution of the Earth-Moon system. Geophysical Journal of the Royal Astronomical Society. 1982, 70 (1): 261–271. Bibcode:1982GeoJ...70..261W. doi:10.1111/j.1365-246X.1982.tb06404.x
 .
.
- ^ C.D. Murray; S.F. Dermott. Solar System Dynamics. Cambridge University Press. 1999: 184.
- ^ Dickinson, Terence. From the Big Bang to Planet X. Camden East, Ontario: Camden House. 1993: 79–81. ISBN 0-921820-71-2.
- ^ Caltech Scientists Predict Greater Longevity for Planets with Life 網際網路檔案館的存檔,存檔日期2012-03-30.
- ^ 26.0 26.1 The reference by H. L. Vacher (2001) (details separately cited in this list) describes this as 'convex outward', whereas older references such as "The Moon's Orbit Around the Sun, Turner, A. B. Journal of the Royal Astronomical Society of Canada, Vol. 6, p. 117, 1912JRASC...6..117T (頁面存檔備份,存於網際網路檔案館)"; and "H Godfray, Elementary Treatise on the Lunar Theory" describe the same geometry by the words concave to the sun.
- ^ Seidelmann, P. Kenneth (編), Explanatory Supplement to the Astronomical Almanac, University Science Books: 701, 1992, ISBN 0-935702-68-7
- ^ 28.0 28.1 28.2 The Orbit of the Moon around the Sun is Convex!. [2022-04-14]. (原始內容存檔於31 March 2004).
- ^ The Moon Always Veers Toward the Sun at MathPages
外部連結
[編輯]- View of the Moon (頁面存檔備份,存於網際網路檔案館) Good diagrams of Moon, Earth, tilts of orbits and axes, courtesy of U. of Arkansas







