小斜方截半立方体
 (按这里观看旋转模型) | |||||
| 类别 | 半正多面体 | ||||
|---|---|---|---|---|---|
| 对偶多面体 | 筝形二十四面体 | ||||
| 识别 | |||||
| 名称 | 小斜方截半立方体 | ||||
| 参考索引 | U10, C22, W13 | ||||
| 鲍尔斯缩写 | sirco | ||||
| 数学表示法 | |||||
| 考克斯特符号 | |||||
| 施莱夫利符号 | rr{4,3} | ||||
| 威佐夫符号 | 3 4 | 2 | ||||
| 康威表示法 | eC aaC aaaT | ||||
| 性质 | |||||
| 面 | 26 | ||||
| 边 | 48 | ||||
| 顶点 | 24 | ||||
| 欧拉特征数 | F=26, E=48, V=24 (χ=2) | ||||
| 组成与布局 | |||||
| 面的种类 | 正三角形 正方形 | ||||
| 面的布局 | 8个{3} (6+12)个{4} | ||||
| 顶点图 | 3.4.4.4 | ||||
| 对称性 | |||||
| 对称群 | Oh群 | ||||
| 特性 | |||||
| - | |||||
| 图像 | |||||
| |||||
在几何学中,小斜方截半立方体,又称为菱方八面体,是一种有18个正方形和8个正三角形的阿基米德立体。小斜方截半立方体共有26个面、48条边以及24个顶点,具有点可递性质,因此既是均匀多面体也是半正多面体。
性质
[编辑]小斜方截半立方体每八条棱可以成为一个正八边形,共可以形成六个独立的正八边形。
体积与表面积
[编辑]边长为的小斜方截半立方体,其表面积和体积如下:.
表面积,
体积。
座标
[编辑]边长为2且几何中心位于原点的小斜方截半立方体,其顶点座标为:
的全排列。边长为1的小斜方截半立方体,其对偶多面体筝形二十四面体的边长为:
- 和
与其他几何体的关联
[编辑]若将小斜方截半立方体扭曲使面不再是正多边形,则它的顶点仍然会保持均匀。他们可以透过将立方体或八面体先截去所有的棱再截去所有的顶点而成,因此所得的多面体会有6个正方形面和12矩形面。他们具有八面体对称并可以形成立方体和八面体之间的连续变形系列,类似于小斜方截半二十面体的变形或由四面体扭曲成的截半立方体。然而,小斜方截半立方体还具有另外的一系列不具有八面体对称而是四面体对称的变形,因此它们与四面体相同旋转对称但不同的反射对称下是不变的,这些变体包含6个长方形面以及16个梯形面。若沿着三阶魔术方块的可转动边缘投射到球体,则会的到一个与小斜方截半立方体类似的拓扑结构,小斜方截半立方体边缘的线条与该种图形完全相同。事实上,有一些魔术方块的变体就是小斜方截半立方体[1]。
小斜方截半立方体能够成三种空间均匀堆砌,但不能独立完成堆砌,都要跟其他立体图行一同完成堆砌。这三种空间均匀堆砌分别为:截棱立方体堆砌、截面斜截立方体堆砌以及截面立方体堆砌。
拆解
[编辑]小斜方截半立方体可以被切割成上下两个正四角帐塔和中间一个正八角柱。若将上下两个正四角帐塔的其中一个水平旋转45度的话,则会形成伪小斜方截半立方体,即异相双四角台塔柱,它与小斜方截半立方体拥有相同的顶点布局:3.4.4.4。
小斜方截半立方体可以看作有三对互相平行的八边形切面,因此上述的切割方式可以从三种不同的方式进行。其切割出来的正四角帐塔是一种詹森多面体。若将其切割出来的图形,其中一个正四角帐塔水平旋转45度之后重新组合则会形成一个看起来与小斜方截半立方体十分相近的不同立体,称为异相双四角台塔柱或伪小斜方截半立方体,其也是詹森多面体的一种。若将中间的正八角柱拿掉的话,小斜方截半立方体会变成同相双四角台塔,而伪小斜方截半立方体会变成异相双四角台塔,这两个多面体也是詹森多面体。而这些属于“异相”的多面体都是四角反棱柱的对称性。

|
 小斜方截半立方体 |
 伪小斜方截半立方体 |
作法
[编辑]将一个立方体(正八面体)十二条棱都切一刀,在八(六)个顶点处也切一刀,就可以得到一个小斜方截半立方体。该动作会先得到一个倒角立方体,然后再顶点处也切一刀后即得到小斜方截半立方体。
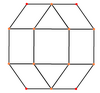
正交投影
[编辑]| 建立于 | 顶点 | 三角形-四边形 交棱 |
四边形-四边形 交棱 |
正方形面 | 正三角形面 | |
|---|---|---|---|---|---|---|
| 图像 | 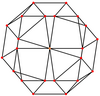
|

|

|
|

|

|
| 投影对称性 | [2] | [2] | [2] | [2] | [4] | [6] |
| 对偶的正交投影 | 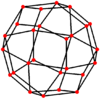
|

|
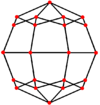
|

|
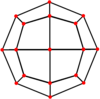
|

|
球面镶嵌
[编辑]
|
 (6) 以正方形为中心 |
 (6) 另一种以正方形为中心 |
 (8) 以正三角形为中心 |
| 平行投影 | 施莱格尔投影 | ||
|---|---|---|---|
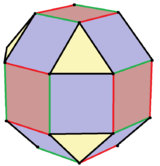 均匀的形状 |
 不均匀的形状 |
 不均匀的形状 |
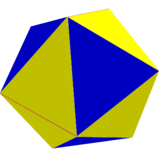 到在极限情况下会 变成一个二十面体 扭棱八面体: 从两个位置之一。 |
 二复合二十面体 从两个交替位置。 |
顶点排布
[编辑]共有三种多面体与小斜方截半立方体有着相同的顶点排布。他们分别为:
 小斜方截半立方体 |
 小立方立方八面体 |
 小斜方六面体 |
 星形截角立方体 |
应用
[编辑]
由于小斜方截半立方体的形状仅由正方形跟正三角形构成,且十分接近球体,绘制或制作都相对简单,因此常出现在各种领域中,如艺术。
煤精印
[编辑]煤精印外表是一个小斜方截半立方体,在正方形面18个,三角形面8个中,其中有14个正方形面上镌刻有印文[2],小斜方截半立方体拥有26个面,也导致了该印章是目前已发现的中国古代多面印章中印面印章[3]。小斜方截半立方体一共有18个正方形面,其中14个正方形面上印有“臣信上疏”、“臣信上章”、“臣信上表”、“臣信启事”、“大司马印”、“大都督印”、“刺史之印”、“柱国之印”、“耶敕”、“信启事”、“信白笺”、“密”、“令”、“独孤信白书”且皆为阴文楷书,它的发现证明早在南北朝时期,古人已经开始在印章中使用楷书,纠正了原先学界关于楷书入印最早为隋唐时期的观点。[4][3]
艺术
[编辑] 小斜方截半立方体出现在1495年卢卡·帕西奥利的肖像画作中[5] |
 达芬奇在帕西奥利神曲的设计 , 1509: "Vigintisexbasium Planum Vacuum".[6] |
较大的小斜方截半立方体出现在1495年卢卡·帕西奥利的肖像画作中(传统上对此画作者有争议,认为是雅各布·德巴尔巴里)。该画作左上角有一个装半满水的小斜方截半立方体形状的玻璃容器。首个有小斜方截半立方体的艺术画作则是出现在达芬奇1509年的帕西奥利神曲。
虽然球形180×360°的全景可以投影到任何多面体,但小斜方截半立方体是一个更简单更且十分近似球体的形状,这种类型的投影,称为斐洛球(英语:Philosphere),可用于全景图合成成软件中。部分能做成实体的全景图合成成软件是利用由单独打印的两个可利用剪刀剪下有留下黏贴处的图像,即把全景图制成小斜方截半立方体的展开图,来做成斐洛球[7]。
游戏与玩具
[编辑]
游戏《自由空间》中的关卡〈钻井机〉和〈黑暗之地〉游戏中的地图形状是一个小斜方截半立方体。
在超级马里奥银河的〈慌张银河〉关卡中也有一个小斜方截半立方体形状的行星。

《音速小子3》的Icecap Zone关卡也有以小斜方截半立方体为特色的柱子。
此外,由于三阶魔术方块的切割处(可旋转的面)与小斜方截半立方体的边缘同构,或者说,将小斜方截半立方体的边缘投影至球体与三阶魔术方块的切割处投影至球体完全一致,因此外型为小斜方截半立方体形式的魔术方块可以是一种三阶魔术方块的变体。
魔术方块在1980年代流行期间,twisty puzzle曾经发售过小斜方截半立方体形式的魔术方块。
魔术方块的变体魔棍玩具在贩售时通常会将其转成小斜方截半立方体的形状出售,12个方块被替换成1:√2的矩形。
Cabela's研发的能“自我修复”的防弹材料如右图,其示范的模形形状与小斜方截半立方体十分接近。
相关多面体及镶嵌
[编辑]| 对称性: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | c{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
|||||||||
| 对偶多面体 | |||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V4.62/63 | V34.4 | V33 | V3.62 | V35 |
参见
[编辑]注释
[编辑]参考文献
[编辑]- Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- Cromwell, P. Polyhedra. United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
- Coxeter, H.S.M.; Longuet-Higgins, M.S.; Miller, J.C.P. Uniform Polyhedra. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. May 13, 1954, 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003.
- de Graaf, J.; van Roij, R.; Dijkstra, M., Dense Regular Packings of Irregular Nonconvex Particles, Phys. Rev. Lett., 2011, 107: 155501, Bibcode:2011PhRvL.107o5501D, arXiv:1107.0603
 , doi:10.1103/PhysRevLett.107.155501
, doi:10.1103/PhysRevLett.107.155501 - Betke, U.; Henk, M., Densest Lattice Packings of 3-Polytopes, Comput. Geom., 2000, 16: 157, doi:10.1016/S0925-7721(00)00007-9
- Torquato, S.; Jiao, Y., Dense packings of the Platonic and Archimedean solids, Nature, 2009, 460: 876, Bibcode:2009Natur.460..876T, PMID 19675649, arXiv:0908.4107
 , doi:10.1038/nature08239
, doi:10.1038/nature08239 - Hales, Thomas C., A proof of the Kepler conjecture, Annals of Mathematics, 2005, 162: 1065, doi:10.4007/annals.2005.162.1065
- ^ Soviet Puzzle Ball. TwistyPuzzles.com. [23 December 2015]. (原始内容存档于2016-03-04).
- ^ 国宝档案2009年第309期——煤精印(上). 央视网. [2016-03-05]. (原始内容存档于2016-03-04).
- ^ 3.0 3.1 国宝档案2009年第310期——煤精印(下). 央视网. [2016-03-05]. (原始内容存档于2016-03-04).
- ^ “天下第一岳父”煤精印. 内蒙古日报. 2011-11-01 [2016-03-12]. (原始内容存档于2016-01-26).
- ^ THE ENIGMA OF LUCA PACIOLI'S PORTRAIT. RitrattoPacioli.it. [2016-02-13]. (原始内容存档于2016-01-29).
- ^ Da divina proportione, 第XXXVI页
- ^ 3-D panorama printing: enter physical reality.... philohome.com. [2016-03-10]. (原始内容存档于2016-03-13).
外部链接
[编辑]- 埃里克·韦斯坦因, 小斜方截半立方体 (参阅阿基米德立体) 于MathWorld(英文)
- Klitzing, Richard. 3D convex uniform polyhedra x3o4x - sirco. bendwavy.org.
- The Uniform Polyhedra (页面存档备份,存于互联网档案馆)
- Virtual Reality Polyhedra (页面存档备份,存于互联网档案馆) The Encyclopedia of Polyhedra
- Editable printable net of a rhombicuboctahedron with interactive 3D view (页面存档备份,存于互联网档案馆)
- Rhombicuboctahedron Star (页面存档备份,存于互联网档案馆) by Sándor Kabai, Wolfram Demonstrations Project.
- Rhombicuboctahedron: paper strips for plaiting (页面存档备份,存于互联网档案馆)
| ||||||||||||
| ||||||||||||||||||||