镜像法 (又称镜像电荷法 )是一种解析静电学 问题的基本工具。对于静电学问题,镜像法将原本问题的某些元素改换为假想电荷 ,同时保证仍然满足定解问题原有的的边界条件 (请参阅狄利克雷边界条件 或诺伊曼边界条件 )。
例如,给定一个由一片无限平面导体 和一个点电荷 构成的物理系统,这无限平面导体可以被视为一片镜子,在镜子里面的镜像电荷 与镜子外面的点电荷,所形成的新系统,可以使得导体平面上的电场垂直于导体,与原本系统等价。借此方法,我们可以将问题简化,很容易地计算出导体外的电势 、导体的表面感应电荷密度 、总感应电荷 等等。
镜像法的有效性是唯一性定理 的必然结果,该定理指出如果指定了在体积 V 的整个区域内的电荷密度和 V 的所有边界上的电位值,区域 V 内的电位唯一确定。另外,应用此结果到高斯定理的微分形式就能表明,在由导体包围的包含电荷密度为 ρ 的体积 V 中,如果每个导体所带电荷已经给出,那么电场是唯一确定的。拥有电势或电场的信息以及相应边界条件,只要在指定区域的电荷分布满足泊松方程并设定正确的边界值,我们就可以把我们考虑的电荷分布换为更容易分析的结构。
[ 1]
唯一性定理 表明,任意能够满足给定条件的解答,是唯一存在的解答。因此,给定条件唯一地决定了这解答。
举例而言,假若,在一个三维空间区域里,电势
ϕ
{\displaystyle \phi }
∇
2
ϕ
=
f
{\displaystyle \nabla ^{2}\phi =f}
而在区域的表面,又满足边界条件
ϕ
=
g
{\displaystyle \phi =g}
其中,
f
{\displaystyle f}
g
{\displaystyle g}
函数 ,
则
ϕ
(
x
,
y
,
z
)
{\displaystyle \phi (x,\,y,\,z)}
唯一性定理适用于以下三种边界情况:
给出了整个边界的势函数;
给出整个边界的势函数的法向导函数;
给出整个边界部分场的势函数和其他部分的势函数的法向导函数; 应用唯一性定理于镜像法,只要问题能够给足上述任意一种边界条件,则求得的电势函数解答必定是唯一的正确解答。
原本系统。位于 xy-平面的是一个接地 的无限平面导体。其上方的点电荷
q
{\displaystyle q}
(
0
,
0
,
a
)
{\displaystyle (0,\,0,\,a)}
镜像法的新系统。坐标是
(
0
,
0
,
−
a
)
{\displaystyle (0,\,0,\,-a)}
−
q
{\displaystyle -q}
举一个简单的例子,如右图所示,设定一个接地 的无限平面导体于 xy-平面,其上方有一个点电荷
q
{\displaystyle q}
(
0
,
0
,
a
)
{\displaystyle (0,\,0,\,a)}
库仑定律 和相关静电理论,这物理系统的各种物理量 ,像导体表面的电荷分布,或点电荷所感受到的作用力,都不是很容易可以计算求得。
应用镜像法,可以将无限平面导体改换成一个镜像电荷,坐标是
(
0
,
0
,
−
a
)
{\displaystyle (0,\,0,\,-a)}
−
q
{\displaystyle -q}
(
x
,
y
,
z
)
,
z
>
0
{\displaystyle (x,\,y,\,z),\ z>0}
在新系统里,应用库仑定律,可以很容易地计算出点电荷所感受到的作用力。
采用圆柱坐标
(
ρ
,
ϕ
,
z
)
{\displaystyle (\rho ,\,\phi ,\,z)}
V
(
ρ
,
z
)
{\displaystyle V(\rho ,\,z)}
方位角
ϕ
{\displaystyle \phi }
V
(
ρ
,
z
)
=
1
4
π
ϵ
0
(
q
ρ
2
+
(
z
−
a
)
2
+
−
q
ρ
2
+
(
z
+
a
)
2
)
{\displaystyle V(\rho ,\,z)={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+(z-a)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+(z+a)^{2}}}}\right)}
根据唯一性定理 ,这解答是原本问题的唯一解答。
无限平面导体的表面电荷密度
σ
(
ρ
)
{\displaystyle \sigma (\rho )}
σ
=
−
ϵ
0
∂
V
∂
z
|
z
=
0
=
−
q
a
2
π
(
ρ
2
+
a
2
)
3
/
2
{\displaystyle \sigma =-\epsilon _{0}{\frac {\partial V}{\partial z}}{\Bigg |}_{z=0}=-\ {\frac {qa}{2\pi (\rho ^{2}+a^{2})^{3/2}}}}
积分表面电荷密度于无限平面导体,可以得到无限平面导体的总感应电量
Q
t
{\displaystyle Q_{t}}
Q
t
{\displaystyle Q_{t}}
=
∫
0
2
π
∫
0
∞
σ
(
ρ
)
ρ
d
ρ
d
θ
{\displaystyle =\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\theta }
=
−
q
a
2
π
∫
0
2
π
d
θ
∫
0
∞
ρ
d
ρ
(
ρ
2
+
a
2
)
3
/
2
{\displaystyle =-\ {\frac {qa}{2\pi }}\int _{0}^{2\pi }d\theta \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\right)^{3/2}}}}
=
−
q
{\displaystyle =-q}
答案非常简单,就是
−
q
{\displaystyle -q}
这问题指引出一个更进阶的问题:给予一对平行的无限平面导体,其中间有一个点电荷,求两片无限平面导体之间的电势?这是一个非常有意思,值得研习的问题[ 2]
所有二面角成
α
=
2
π
n
{\displaystyle \alpha ={\frac {2\pi }{n}}}
n
{\displaystyle n}
n
−
1
{\displaystyle n-1}
[来源请求]
延伸至两个点电荷的物理系统。 镜像法可以延伸至两个或多于两个点电荷。只要对于每一个点电荷,都添加一个对应的镜像电荷。根据叠加原理 ,总电势等于所有点电荷、镜像电荷产生的电势的总和。在 xy-平面的任意一位置,点电荷产生的电势会与其镜像电荷产生的电势相抵消。因此,在 xy-平面的任意一位置,总电势等于零,满足边界条件。
图右展示一个物理系统案例,里面有两个真实的点电荷和一个无限平面导体,两个点电荷的坐标分别是
(
x
1
,
y
1
,
z
1
)
{\displaystyle (x_{1},\,y_{1},\,z_{1})}
(
x
2
,
y
2
,
z
2
)
{\displaystyle (x_{2},\,y_{2},\,z_{2})}
q
1
{\displaystyle q_{1}}
q
2
{\displaystyle q_{2}}
(
x
1
,
y
1
,
−
z
1
)
{\displaystyle (x_{1},\,y_{1},\,-z_{1})}
(
x
2
,
y
2
,
−
z
2
)
{\displaystyle (x_{2},\,y_{2},\,-z_{2})}
−
q
1
{\displaystyle -q_{1}}
−
q
2
{\displaystyle -q_{2}}
假设,在无限平面导体上方,有一个电偶极子 ,其电偶极矩 是
M
=
(
M
x
,
M
y
,
M
z
)
{\displaystyle \mathbf {M} =(M_{x},\,M_{y},\,M_{z})}
(
x
,
y
,
z
)
{\displaystyle (x,\,y,\,z)}
M
′
=
(
M
x
,
M
y
,
−
M
z
)
{\displaystyle \mathbf {M} '=(M_{x},\,M_{y},\,-M_{z})}
(
x
,
y
,
−
z
)
{\displaystyle (x,\,y,\,-z)}
应用镜像法于半径为
R
{\displaystyle R}
球坐标系 的原点于圆球壳壳心。绿点是点电荷
q
{\displaystyle q}
P
{\displaystyle \mathbf {P} }
−
q
R
/
p
{\displaystyle -qR/p}
R
2
/
p
{\displaystyle R^{2}/p}
r
=
R
{\displaystyle r=R}
镜像法也可以应用于圆球壳导体[ 3]
如图右,采用原点位于圆球壳壳心的球坐标系 。被置于真空中的接地 的圆球壳,其半径为
R
{\displaystyle R}
q
{\displaystyle q}
P
{\displaystyle \mathbf {P} }
−
q
R
/
p
{\displaystyle -qR/p}
R
2
/
p
{\displaystyle R^{2}/p}
r
{\displaystyle \mathbf {r} }
叠加 为
4
π
ϵ
0
V
(
r
)
=
q
|
r
1
|
+
(
−
q
R
/
p
)
|
r
2
|
=
q
r
2
+
p
2
−
2
r
⋅
p
+
(
−
q
R
/
p
)
r
2
+
R
4
p
2
−
2
R
2
p
2
r
⋅
p
{\displaystyle 4\pi \epsilon _{0}V(\mathbf {r} )={\frac {q}{|\mathbf {r} _{1}|}}+{\frac {(-qR/p)}{|\mathbf {r} _{2}|}}={\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}+{\frac {(-qR/p)}{\sqrt {r^{2}+{\frac {R^{4}}{p^{2}}}-{\frac {2R^{2}}{p^{2}}}\mathbf {r} \cdot \mathbf {p} }}}}
经过一番运算,可以得到
V
(
r
)
=
1
4
π
ϵ
0
[
q
r
2
+
p
2
−
2
r
⋅
p
−
q
r
2
p
2
R
2
+
R
2
−
2
r
⋅
p
]
{\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}
请注意,在圆球壳(
r
=
R
{\displaystyle r=R}
r
<
R
{\displaystyle r<R}
V
(
r
)
{\displaystyle V(\mathbf {r} )}
r
>
R
{\displaystyle r>R}
V
(
r
)
{\displaystyle V(\mathbf {r} )}
σ
{\displaystyle \sigma }
天顶角
θ
{\displaystyle \theta }
σ
(
θ
)
=
ϵ
0
∂
V
∂
r
|
r
=
R
=
−
q
(
R
2
−
p
2
)
4
π
R
(
R
2
+
p
2
−
2
p
R
cos
θ
)
3
/
2
{\displaystyle \sigma (\theta )=\epsilon _{0}{\frac {\partial V}{\partial r}}{\Bigg |}_{r=R}={\frac {-q(R^{2}-p^{2})}{4\pi R(R^{2}+p^{2}-2pR\cos \theta )^{3/2}}}}
积分感应电荷密度于所有立体角 ,则可以得到在圆球壳的总感应电量
Q
t
{\displaystyle Q_{t}}
Q
t
=
∫
0
π
d
θ
∫
0
2
π
d
ϕ
σ
(
θ
)
R
2
sin
θ
=
−
q
{\displaystyle Q_{t}=\int _{0}^{\pi }d\theta \int _{0}^{2\pi }d\phi \,\,\sigma (\theta )R^{2}\sin \theta =-q}
由于总感应电量与点电荷电量的代数和 等于零,所以整个物理系统的总电量等于零。圆球壳导体能够除去点电荷所造成的非球形对称性 。在圆球壳以外的物理是球形对称的。应用高斯定律 ,可以计算出电场
E
{\displaystyle \mathbf {E} }
E
=
0
{\displaystyle \mathbf {E} =\mathbf {0} }
假设圆球壳不接地,则圆球壳外表面的感应电荷密度是
σ
=
q
/
4
π
R
2
{\displaystyle \sigma =q/4\pi R^{2}}
圆球壳外,离圆心距离为
r
{\displaystyle r}
E
{\displaystyle \mathbf {E} }
E
=
q
4
π
ϵ
0
r
2
r
^
{\displaystyle \mathbf {E} ={\frac {q}{4\pi \epsilon _{0}r^{2}}}{\hat {\mathbf {r} }}}
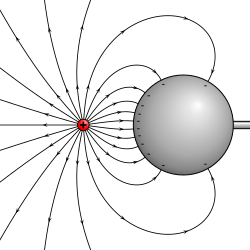
接地圆球导体壳外的电场线。 请注意,这问题的逆反问题也可以用镜像法解析。在一个半径为
R
{\displaystyle R}
q
{\displaystyle q}
p
{\displaystyle \mathbf {p} }
p
{\displaystyle p}
−
q
R
/
p
{\displaystyle -qR/p}
(
R
2
/
p
2
)
p
{\displaystyle (R^{2}/p^{2})\mathbf {p} }
镜像法对于电偶极矩 的计算公式比较复杂。假若我们将电偶极子 视为一对距离很近的点电荷,则镜像电偶极子 的电量和电偶极矩都会有所改变。给予电偶极子的电偶极矩为
M
{\displaystyle \mathbf {M} }
p
{\displaystyle \mathbf {p} }
R
{\displaystyle R}
(
R
2
/
p
2
)
p
{\displaystyle (R^{2}/p^{2})\mathbf {p} }
q
′
=
R
p
⋅
M
p
3
{\displaystyle q'={\frac {R\mathbf {p} \cdot \mathbf {M} }{p^{3}}}}
电偶极矩为
M
′
=
R
3
[
−
M
p
3
+
2
p
(
p
⋅
M
)
p
5
]
{\displaystyle \mathbf {M} '=R^{3}\left[-{\frac {\mathbf {M} }{p^{3}}}+{\frac {2\mathbf {p} (\mathbf {p} \cdot \mathbf {M} )}{p^{5}}}\right]}
镜像法的圆球壳计算方式直接地引导出反演法 。采用球坐标
(
r
,
θ
,
ϕ
)
{\displaystyle (r,\,\theta ,\,\phi )}
调和函数
Φ
(
r
,
θ
,
ϕ
)
{\displaystyle \Phi (r,\,\theta ,\,\phi )}
R
{\displaystyle R}
Φ
′
(
r
,
θ
,
ϕ
)
=
R
r
Φ
(
R
2
r
,
θ
,
ϕ
)
{\displaystyle \Phi '(r,\,\theta ,\,\phi )={\frac {R}{r}}\Phi \left({\frac {R^{2}}{r}},\,\theta ,\,\phi \right)}
给予一集合的点电荷,位置和电量分别为
(
r
i
,
θ
i
,
ϕ
i
)
{\displaystyle (r_{i},\,\theta _{i},\,\phi _{i})}
q
i
{\displaystyle q_{i}}
Φ
{\displaystyle \Phi }
Φ
′
{\displaystyle \Phi '}
(
R
2
/
r
i
,
θ
i
,
ϕ
i
)
{\displaystyle (R^{2}/r_{i},\,\theta _{i},\,\phi _{i})}
R
q
i
/
r
i
{\displaystyle Rq_{i}/r_{i}}
ρ
(
r
,
θ
,
ϕ
)
{\displaystyle \rho (r,\,\theta ,\,\phi )}
Φ
{\displaystyle \Phi }
Φ
′
{\displaystyle \Phi '}
ρ
′
(
r
,
θ
,
ϕ
)
=
(
R
/
r
)
5
ρ
(
R
2
/
r
,
θ
,
ϕ
)
{\displaystyle \rho '(r,\,\theta ,\,\phi )=(R/r)^{5}\rho (R^{2}/r,\,\theta ,\,\phi )}
帕松方程的唯一性定理 (Uniqueness theorem for Poisson's equation )恩绍定理 (Earnshaw's theorem )互易定理 (Reciprocity (electromagnetism))多极展开
^
David J. Griffiths. Introduction to Electrodynamics (4th Ed.). Glenview, IL: Pearson. 2013: 121. ISBN 0-321-85656-2
^ Dick, B. G., Images and the Point Charge-Capacitor Problem, American Journal of Physics, 1973, 41 (11): pp. 1289–1290 ^ Tikhonov, A. N.; Samarskii, A. A. Equations of Mathematical Physics. New York: Dover Publications. 1963. ISBN 0-486-66422-8















































![{\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52743d0a81a388b2953818dd92243520c7b21231)

















![{\displaystyle \mathbf {M} '=R^{3}\left[-{\frac {\mathbf {M} }{p^{3}}}+{\frac {2\mathbf {p} (\mathbf {p} \cdot \mathbf {M} )}{p^{5}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3546c8e9d0d782e6a1f35dfbaf85e9cc0798b03)











