电磁波

电磁波(英文:Electromagnetic wave)是指同相振荡且互相垂直的电场与磁场,是一种非机械波,在空间中以波的形式传递能量和动量,其传播方向垂直于电场与磁场的振荡方向。
电磁波不需要依靠介质进行传播,在真空中其传播速度为光速。电磁波可按照频率分类,从低频率到高频率,主要包括无线电波、兆赫辐射、微波、红外线、可见光、紫外线、X射线和伽马射线。人眼可接收到的电磁波,波长大约在380至780nm之间,称为可见光。
发现历史
[编辑]
在可见光波长以外的电磁辐射被发现于19世纪初期。红外线辐射的发现归因于天文学家威廉·赫歇尔,他于1800年在伦敦皇家学会发表了他的成果。[1]
电磁波首先由詹姆斯·马克士威于1865年预测出来,而后由德国物理学家海因里希·赫兹于1887年至1888年间在实验中证实存在。[2][3]马克士威推导出电磁波方程式,一种波动方程式,这清楚地显示出电场和磁场的波动本质。因为电磁波方程式预测的电磁波速度与光速的测量值相等,马克士威推论光波也是电磁波[4][5]:283。无线电波被海因里希·赫兹在1887年第一个刻意产生,使用电路计算出比可见光低得多的频率上产生振荡,随之产生了由麦克斯韦方程所建议的振荡电荷和电流。赫兹还开发检测这些电波的方法,并产生和特征化这些后来被称为无线电波和微波。[6]:286,7
威廉·伦琴发现并命名了X射线。 在1895年11月8日的应用于真空管上的高电压试验后,他注意到在附近的镀膜玻璃板的荧光。在一个月内,他发现了X射线的主要性质。[6]:307
概念
[编辑]
电动力学专门研究电磁波的物理行为,是电磁学的分支。在电动力学里,根据马克士威方程组,随著时间变化的电场产生了磁场,反之亦然。因此,一个振荡中的电场会产生振荡的磁场,而一个振荡中的磁场又会产生振荡的电场,这样子,这些连续不断同相振荡的电场和磁场共同地形成了电磁波[7]:326[8]:894-897。
电场,磁场都遵守叠加原理。[9]:9因为电场和磁场都是向量场,所有的电场向量和磁场向量都适合做向量加运算。例如,一个行进电磁波,入射于一个介质,会引起介质内的电子振荡,因而使得它们自己也发射电磁波,因而造成折射或绕射等等现象[8]:959-968。
在非线性介质内(例如,某些晶体),电磁波会与电场或磁场产生交互作用,这包括法拉第效应[10]:366-368、克尔效应等等[11]。
当电磁波从一种介质入射于另一种介质时,假若两种介质的折射率不相等,则会产生折射现象,电磁波的方向和速度会改变。斯涅尔定律专门描述折射的物理行为[7]:388。

假设,由很多不同频率的电磁波组成的光波,从空气入射于棱镜。而因为菱镜内的材料的折射率跟电磁波的频率有关,会产生色散现象:光波会色散成一组可观察到的电磁波谱[7]:398-405。
波动理论
[编辑]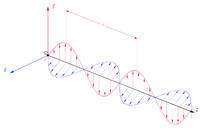
波是由很多前后相继的波峰和波谷所组成,两个相邻的波峰或波谷之间的距离称为波长。电磁波的波长有很多不同的尺寸,从非常长的无线电波(有一个足球场那么长)到非常短的伽马射线(比原子半径还短)[8]:890。
描述光波的一个很重要的物理参数是频率。一个波的频率是它的振荡率,国际单位制单位是赫兹。每秒钟振荡一次的频率是一赫兹。频率与波长成反比:
- ;
其中,是波速(在真空里是光速;在其它介质里,小于光速),是频率,是波长。
当波从一个介质传播至另一个介质时,波速会改变,但是频率不变[8]:961。
干涉是两个或两个以上的波,叠加形成新的波样式。假若这几个电磁波的电场同方向,磁场也同方向,则这干涉是建设性干涉;反之,则是摧毁性干涉[8]:959-962。
电磁波的能量,又称为辐射能。这能量,一半储存于电场,另一半储存于磁场。用方程式表达[8]:897-899:
- ;
其中,是单位体积的能量,是电场数值大小,是磁场数值大小,是电常数,是磁常数。
传播速度
[编辑]呈加速运动的电荷或随著时间而变化的电磁场,会产生电磁波。在自由空间里,电磁波以光速传播。准确的计算其物理行为必须引用推迟时间的概念。这会增加电场和磁场的表达式的复杂程度(参阅杰斐缅柯方程式)。这些多加的项目详细地描述电磁波的物理行为。当任意一根导线(或别种导电体,像天线)传导交流电的时候,同频率的电磁波也会被发射出来[7]。
电磁波必然遵守一条定则:不管观察者的速度有多快或多慢,相对于观察者,电磁波永远以光速传播于真空。爱因斯坦从这洞察发展出狭义相对论,成为狭义相对论的第二条基本原理。
在其它不同于真空的介质内,电磁波传播的速度会小于光速。一个介质的折射率是光速与电磁波传播于介质的速度的比例:
- 。
电磁波谱
[编辑]按照波长长短,从长波开始,电磁波可以分类为无线电波、微波、红外线、可见光、紫外线、X-射线和伽马射线等等。普通实验使用的光谱仪就足以分析从2 奈米到2500 奈米波长的电磁波。使用这种仪器,可以得知物体、气体或甚至恒星的详细物理性质。这是天文物理学的必备仪器。例如,因为超精细分裂,氢原子会发射波长为21.12公分的无线电波[12]。
人类眼睛可以观测到波长大约在400 奈米和700 奈米之间的电磁波,称为‘可见光’。
每一种电极性分子,会对应著某些特定频率的微波,使得电极性分子随著振荡电场一起旋转,这机制称为电介质加热(dielectric heating)。由于这种机制(不是热传导机制),电极性分子会吸收微波的能量。微波炉就是应用这运作原理,通过水分子的旋转,更均匀地将食物加热,减少等候时间。
从电磁理论推导
[编辑]马克士威方程组可以描述电磁波的普遍物理现象。在自由空间里,源项目等于零(源电荷等于零,源电流等于零)。除了没有任何事发生的解以外(电场和磁场都等于零),方程式仍旧允许不简单的解,电场和磁场随著时间和位置变化[7]。采用国际单位制,处于自由空间状况的马克士威方程组表达为
- 、(1)
- 、(2)
- 、(3)
- ;(4)
满足上述条件的一个解是,然而这是一个平庸解,并没有甚么有意思的物理意义。若想得到有意思的解答,必须稍做一些运算。取公式(2)的旋度,
- 。(5)
应用一个向量恒等式,再将公式(1)代入,则可得到:
- 。(6)
应用公式(4),公式(5)右边变为
- 。(7)
将公式(6)和(7)代回公式(5),可以得到电场的波动方程式:
。
使用类似的方法,可以得到磁场的波动方程式:
。
这两个方程式就是真空的电磁波方程式,描述传播于真空的电磁波。更简易地表达,
- 、
- ;
其中,是达朗白算符,是波动传播的速度。
在自由空间里,是光速。马克士威方程组连结了三个基本物理量:真空电容率、真空磁导率和光速。这组关系是在麦克斯韦的电动力学发展之前就由威廉·爱德华·韦伯与鲁道夫·科尔劳施发现,但麦克斯韦是首个创造与波在光速传播相一致的场论的人。
前面已经找到了两个方程式。但是马克士威方程组有四个方程式,所以,还有很多重要的讯息隐藏在这个方程式里。思考一个一般的电场向量波动的解,
- ;
其中,是常数振幅,是任意二次可微函数,是波向量,是位置向量,是角频率。
波动方程式的通解是。也就是说,
- 。
将电场的公式代入公式(1):
- 。
只要电场垂直于波向量(波动传播的方向),这函数形式的电场必定满足马克士威方程组:
- 。
再将电场的公式代入公式(2):
- 。
所以,电场与其对应磁场的关系为:
- 。
在自由空间内,电磁波不只是有以光速传播的性质,电磁波的电场部分和磁场部分有特定的相对定向、相对大小。它们之间的相位一样。电场,磁场,波动传播的方向,都互相垂直于对方。波动传播的方向是。
从电磁波传播的方向看去,电场或许是以上下的方式震荡,而磁场以左右的方式震荡。但若将这图样旋转90度,则电场以左右的方式震荡,而磁场以上下的方式震荡,而波动传播的方向仍旧相同。这是波动方程式的另一种解答。对于波动同样传播的方向,这定向的任意性现象称为偏振[7]。
参见
[编辑]参考文献
[编辑]- ^ Philosophical Transactions of the Royal Society of London, Vol. 90 (1800), pp. 284-292, http://www.jstor.org/stable/info/107057
- ^ Encyclopædia Britannica Online. James Clerk Maxwell. Encyclopædia Britannica. [2009-08-24]. (原始内容存档于2009-08-31) (英语).
- ^ Encyclopædia Britannica Online. Heinrich Hertz. Encyclopædia Britannica. [2009-08-25]. (原始内容存档于2009-09-01) (英语).
- ^ 马克士威, 詹姆斯, A dynamical theory of the electromagnetic field (pdf), Philosophical Transactions of the Royal Society of London, 1865, 155: 459–512 [2019-03-19], (原始内容存档 (PDF)于2011-07-28)
- ^ Whittaker, E. T., A history of the theories of aether and electricity. Vol 1, Nelson, London, 1951
- ^ 6.0 6.1 詹姆士·金斯 (1947) The Growth of Physical Science, link from Internet Archive
- ^ 7.0 7.1 7.2 7.3 7.4 7.5 Griffiths, David J. Introduction to Electrodynamics (3rd ed.). Prentice Hall. 1998: pp. 364–374, 416–471. ISBN 0-13-805326-X.
- ^ 8.0 8.1 8.2 8.3 8.4 8.5 Halliday, David; Robert Resnick, Jearl Walker. Fundamental of Physics 7th. USA: John Wiley and Sons, Inc. 2005. ISBN 0-471-23231-9.
- ^ Jackson, John David, Classical Electrodynamic 3rd., USA: John Wiley & Sons, Inc., 1999, ISBN 978-0-471-30932-1
- ^ Hecht, Eugene, Optics 4th, United States of America: Addison Wesley, 2002, ISBN 0-8053-8566-5 (英语)
- ^ Weinberger, P., John Kerr and his Effects Found in 1877 and 1878 (PDF), Philosophical Magazine Letters: 897–907, [2019-03-19], (原始内容存档 (PDF)于2020-04-08)
- ^ Griffiths, David J., Hyperfine splitting in the ground state of hydrogen (PDF), American Journal of Physics, August 1982, 50 (8): pp. 698 [2019-03-19], (原始内容存档 (PDF)于2020-05-12)
外部链接
[编辑]- Clemson University的网页:Electromagnetic Radiation。
- Project PHYSNET (页面存档备份,存于互联网档案馆)的网页: Electromagnetic Waves from Maxwell's Equations (页面存档备份,存于互联网档案馆)。













































