大立方截半立方體

大立方截半立方體

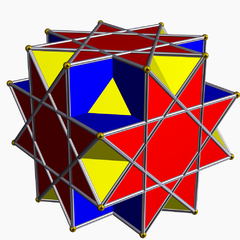類別	星形均勻多面體
對偶多面體	大六角二十四面體
識別
名稱	大立方截半立方體
參考索引	U14, C50, W77
鮑爾斯縮寫	gocco
數學表示法
威佐夫符號	3 4 | 4/3 4 3/2 | 4
性質
面	20
邊	48
頂點	24
歐拉特徵數	F=20, E=48, V=24 （χ=-4）
組成與佈局
面的種類	8個正三角形{3} 6個正方形{4} 6個八角星{8/3}
面的佈局	8{3}+6{4}+6{8/3}
頂點圖	3.8/3.4.8/3
對稱性
對稱群	Oh, [4,3], *432
圖像
3.8/3.4.8/3 （頂點圖） 大六角二十四面體 （對偶多面體）

在幾何學中，大立方截半立方體是一種非凸均勻多面體，屬於星形多面體，其索引為U₁₄。

性質

大立方截半立方體由20個面、48條邊和24個頂點組成，二十個面中，有8個正三角形、6個正方形和6個八角星。其每個頂點都是1個三角形、1個正方形和2個八角星的公共頂點。

大立方截半立方體的凸包是截角立方體。

尺寸

若大立方截半立方體的邊長為單位長，則其外接球半徑為：

$R={\frac {\sqrt {5-2{\sqrt {2}}}}{2}}\approx 0.7368128791$

體積$V$與表面積$A$為：

$V={\frac {8{\sqrt {2}}-6}{3}}\approx 1.77123616633$

$A=-6+12{\sqrt {2}}+2{\sqrt {3}}\approx 14.4346643636$

二面角

大立方截半立方體有兩種二面角，分別為八角星和正方形的二面角以及八角星和三角形的二面角。其中八角星和正方形的二面角為直角，八角星和三角形的二面角為負三平方根倒數的反餘弦值。

$\angle$八角星$,$正方形$\,=90^{\circ }$

$\angle$八角星$,$三角形$\,=\arccos \left(-{\frac {1}{\sqrt {3}}}\right)\approx 2.18627604\approx 125.26438968^{\circ }$

頂點座標

邊長為1的大立方截半立方體的頂點座標為：

$(\pm {\frac {1}{2}},\pm {\frac {1}{2}},\pm {\frac {{\sqrt {2}}-1}{2}})$

$(\pm {\frac {{\sqrt {2}}-1}{2}},\pm {\frac {1}{2}},\pm {\frac {1}{2}})$

$(\pm {\frac {1}{2}},\pm {\frac {{\sqrt {2}}-1}{2}},\pm {\frac {1}{2}})$

分類

由於大立方截半立方體的頂點圖為梯形且具備點可遞的特性，同時，其存在自相交的面，因此大立方截半立方體是一種自相交擬擬正多面體（Self-Intersecting Quasi-Quasi-Regular Polyhedra）。自相交擬擬正多面體一共有12種，除了小雙三角十二面截半二十面體外，其餘由阿爾伯特·巴杜羅（Albert Badoureau）於1881年發現並描述。

自相交擬擬正多面體
（Self-Intersecting Quasi-Quasi-Regular Polyhedra）

小立方立方八面體	大立方截半立方體	非凸大斜方截半立方體	小十二面截半二十面體
大十二面截半二十面體	小雙三角十二面截半二十面體	大雙三角十二面截半二十面體	二十面化截半大十二面體
小二十面化截半二十面體	大二十面化截半二十面體	斜方截半大十二面體	非凸大斜方截半二十面體

正交投影

下圖顯示了三種不同方位大立方截半立方體的正交投影的骨架圖：

對偶多面體

主條目：大六角二十四面體

大立方截半立方體的對偶多面體是一種由24個互相相交的鳶形組成的星形多面體，稱為大六角二十四面體。

相關多面體

大立方截半立方體與截角立方體和另外兩個均勻多面體有着相同的頂點佈局。其亦與非凸大斜方立方八面體和大斜方立方體有着相同的稜佈局。

截角立方體

非凸大斜方立方八面體

大立方截半立方體

大斜方立方體

對偶複合體

大立方截半立方體與其對偶的複合體為複合大立方截半立方體大六角二十四面體。其共有44個面、96條邊和44個頂點，其尤拉示性數為-8，虧格為5，具有6個非凸面。

外部連結

• 埃里克·韋斯坦因. 大立方截半立方體. MathWorld.