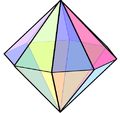
八角柱

正八角柱

类别	柱体 柱状均匀多面体
对偶多面体	双八角锥
识别
名称	正八角柱
参考索引	U76(f)
鲍尔斯缩写	op
数学表示法
考克斯特符号
施莱夫利符号	t{2,8} tr{4,2} s2{2,8} {8}×{} t{4}×{}
威佐夫符号	2 8 | 2
康威表示法	P8
性质
面	10
边	24
顶点	16
欧拉特征数	F=10, E=24, V=16 （χ=2）
组成与布局
面的种类	2个八边形 8个正方形
面的布局	8{4}+2{8}
顶点图	4.4.8
对称性
对称群	D8h, [8,2], (*822), order 32
旋转对称群	D8, [8,2]+, (822), order 16
特性
凸、 zonohedron
图像
4.4.8 （顶点图） 双八角锥 （对偶多面体） （展开图）

在几何学中，八角柱是一种多面体，是柱体的一种，是指底面是八边形的柱体，也是第六种有无限多成员的柱体集合（八角柱包含所有底面是八边形的柱体，即是是凹八边形）。所有八角柱都有10个面，24个边和16个顶点。所有八角柱都是十面体。

如果八角柱每个面都是正多边形，则它是半正多面体。

小斜方截半立方体切去相对的两个正四角帐塔就可以得到一个八角柱。

性质

体积

若一正八角柱的边长皆为1，则八角柱的体积为：

$V=2+2{\sqrt {2}}$

表面积

若一正八角柱的边长皆为1，则八角柱的表面积为：

$V=12+4{\sqrt {2}}$

对称性

图像
对称群	D4h, [2,4], (*422)	D4d, [2+,8], (2*4)
Constructiopn	tr{4,2} or t{4}×{},	s2{2,8},

三维镶嵌和多胞体

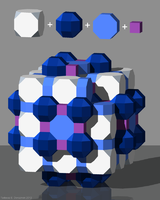
有正八角柱的三维镶嵌:

截角四角柱堆砌	大斜方截半正方体堆砌	小斜方截半正方体堆砌

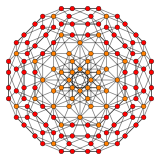
有胞是正八角柱的多胞体:

大斜方截半超立方体	小斜方截半超立方体

在其他领域

• 在光学上，八角柱的棱镜被用于在电影放映机产生不闪烁的图像。
• 十三行博物馆的主要建筑物是一个斜八角柱，象征时间久远遗迹毁坏无法还原的历史真相。

图中棕色建筑物即斜八角柱的十三行博物馆

相关多面体与镶嵌

正多边形柱体系列

对称群	3	4	5	6	7	8	9	10	11	12
[2n,2] [n,2] [2n,2+]
图像
球面多面体
图像

柱体形式半正镶嵌系列：

球面镶嵌		柱体							欧式镶嵌 仿紧空间	双曲镶嵌 非紧空间
t{2,1}	t{2,2}	t{3,2}	{4,2}	t{5,2}	t{6,2}	t{7,2}	t{8,2}	...	t{2,∞}	t{2,iπ/λ}

大斜方截半四阶多面体和镶嵌系列： 4.8.2n

对称群 *n42 [n,4]	球面镶嵌		欧氏镶嵌	紧凑型双曲镶嵌				仿紧空间	非紧空间
	*242 [2,4] D4h	*342 [3,4] Oh	*442 [4,4] P4m	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[iπ/λ,4]
大斜方截半 顶点	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞	4.8.∞
考克斯特纪号 施莱夫利符号	tr{2,4}	tr{3,4}	tr{4,4}	tr{5,4}	tr{6,4}	tr{7,4}	tr{8,4}	tr{∞,4}	tr{iπ/λ,4}
大斜方截半 对偶	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞	V4.8.∞
考克斯特纪号

参考文献

• 埃里克·韦斯坦因. Octagonal prism. MathWorld. 

外部链接

• Interactive model of an Octagonal Prism