 算术平方根的数学表示式
算术平方根的数学表示式
在数学中,一个数 的平方根
的平方根 指的是满足
指的是满足 的数,即平方结果等于
的数,即平方结果等于 的数。例如,4和-4都是16的平方根,因为
的数。例如,4和-4都是16的平方根,因为 。
。
任意非负实数 都有唯一的非负平方根,称为算术平方根或主平方根(英语:principal square root),记为
都有唯一的非负平方根,称为算术平方根或主平方根(英语:principal square root),记为 ,其中的符号
,其中的符号 称作根号。例如,9的算术平方根为3,记作
称作根号。例如,9的算术平方根为3,记作  ,因为
,因为 并且3非负。被求平方根的数称作被开方数(英语:radicand),是根号下的数字或者表达式,即例子中的数字9。
并且3非负。被求平方根的数称作被开方数(英语:radicand),是根号下的数字或者表达式,即例子中的数字9。
正数 有两个互为相反数的平方根:正数
有两个互为相反数的平方根:正数 与负数
与负数 ,可以将两者一起记为
,可以将两者一起记为 。
。
负数的平方根在复数系中有定义。而实际上,对任何定义了开平方运算的数学对象都可考虑其“平方根”(例如矩阵的平方根)。
- 在MicroSoft的试算表软件Excel与大部分编程语言中以 "sqrt()"表示求算术平方根。
耶鲁大学的巴比伦藏品YBC 7289是一块泥板,制作于前1800年到前1600年之间。泥板上是一个画了两条对角线正方形,标注了 的六十进制数字 1;24,51,10。[1]六十进制的 1;24,51,10 即十进制的 1.41421296,精确到了小数点后5位(1.41421356...)。
的六十进制数字 1;24,51,10。[1]六十进制的 1;24,51,10 即十进制的 1.41421296,精确到了小数点后5位(1.41421356...)。
莱因德数学纸草书大约成书于前1650年,内容抄写自更早年代的教科书。书中展示了埃及人使用反比法求平方根的过程。[2]
古印度的《绳法经》大约成书于前800年到前500年之间,书中记载了将2的平方根的计算精确到小数点后5位的方法。
古希腊的《几何原本》大约成书于前380年,书中还阐述了如果正整数不是完全平方数,那么它的平方根就一定是无理数——一种无法以两个整数的比值表示的数(无法写作m/n,其中m和n是整数)。[3]
中国的《书》成书于汉朝(约前202年到前186年之间),书中介绍了使用盈不足术求平方根的方法。
古代未有划一的平方根符号时,人们通常使用他们语言内开方这个字的首个字母的变型作为开方号。
中世纪时,拉丁语中的latus(正方形边)的首个字母“L”被不少欧洲人采用;亨利·布里格斯在其著作《Arithmetica Logarithmica》中则用横线当成latus的简写,在被开方的数下画一线。
最有影响的是拉丁语的radix(平方根),1220年Leconardo在《Practica geometriae》中使用℞(R右下角的有一斜划,像P和x的合体);⎷(没有上面的横划)是由克里斯托费尔·鲁登道夫在1525年的书Coss首次使用,据说是小写r的变型;后来数学家笛卡尔给其加上线括号,但与前面的方根符号是分开的(即“⎷‾”),因此在复杂的式子中它显得很乱。直至18世纪中叶,数学家卢贝将前面的方根符号与线括号一笔写成,并将根指数写在根号的左上角,以表示高次方根(当根指数为2时,省略不写),从而形成了现在人们熟知的开方运算符号![{\displaystyle {\sqrt[{n}]{\,\,}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddcb8a480722f2e988fb8ebe5dfd905140a9a52a) 。
。
 函数
函数 图,半抛物线与垂直准线。
图,半抛物线与垂直准线。
 的平方根亦可用指数表示,如:
的平方根亦可用指数表示,如:

 的绝对值可用
的绝对值可用 的算数平方根表示:
的算数平方根表示:

若正整数 是平方数,则其平方根是整数。若正整数
是平方数,则其平方根是整数。若正整数 不是平方数,则其平方根是无理数。
不是平方数,则其平方根是无理数。
对于正数 、
、 ,以下式成立:
,以下式成立:

正数和负数的平方都是正数,0的平方是0,因此负数没有实数平方根。然而,我们可以把我们所使用的数字集合扩大,加入负数的平方根,这样的集合就是复数。首先需要引入一个实数集之外的新数字,记作 (也可以记作
(也可以记作 ,比如电学场景中
,比如电学场景中 一般表示电流),称之为虚数单位,定义即为
一般表示电流),称之为虚数单位,定义即为 ,故
,故 是-1的平方根,而且
是-1的平方根,而且 ,所以
,所以 也是-1的平方根。通常称-1的算术平方根是
也是-1的平方根。通常称-1的算术平方根是 ,如果
,如果 是任意非负实数,则
是任意非负实数,则 的算术平方根就是:
的算术平方根就是:

例如-5的平方根有两个,它们分别为 和
和 。
。
之所以等式右侧(包括其对应的负值)是 的算术平方根,是因为:
的算术平方根,是因为:

负数的两个平方根为一对共轭的纯虚数。
对于负数 、
、 ,以下式成立:
,以下式成立:

 复数平面中,
复数平面中, 的两个平方根
的两个平方根
虚数 的算术平方根可以根据以下公式计算:
的算术平方根可以根据以下公式计算:

这个公式可以通过用代数方法推导,只需找到特定的实数 和
和 ,满足
,满足

就可以得到方程组

的解:

其中,算术平方根即为

这个公式还可以通过棣莫弗公式得到,设

就可以推出
![{\displaystyle {\begin{aligned}{\sqrt {i}}&=\left[\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)\right]^{\frac {1}{2}}\\&=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)\\&={\frac {\sqrt {2}}{2}}+i{\frac {\sqrt {2}}{2}}\\&={\frac {\sqrt {2}}{2}}(1+i)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f86b3b7203a50d96454199f6b6b0ca30d029303)
 极坐标下,复数
极坐标下,复数 的几个方根
的几个方根
对于任何一个非零的复数 都存在两个复数
都存在两个复数 使得
使得 。
。
首先,我们将复数 看作是平面上的点,即笛卡尔坐标系中的
看作是平面上的点,即笛卡尔坐标系中的 点。这个点也可以写作极坐标的
点。这个点也可以写作极坐标的 ,其中
,其中 ,是该点到坐标原点的距离,
,是该点到坐标原点的距离, 则是从原点到该点的直线与实数坐标轴(
则是从原点到该点的直线与实数坐标轴( 轴)的夹角。复分析中,通常把该点记作
轴)的夹角。复分析中,通常把该点记作 。如果
。如果

那么我们将 的算术平方根定义为:
的算术平方根定义为:

因此,平方根函数除了在非正实数轴上以外是处处全纯的。 的泰勒级数也适用于复数
的泰勒级数也适用于复数 。
。
上面的公式还可以用三角函数的形式表达:

如果使用笛卡尔坐标的形式表达复数 z,其算术平方根可以使用如下公式:[4][5]

其中,方根虚部的符号与被开方数虚部的符号相同(为0时取正);主值实部永远非负。
在虚数里,平方根函数的值不是连续的,以下等式不一定成立:



所以这是错误的:

例:若 ,
,
数学史中,最重要的平方根可以说是 ,它代表边长为1的正方形的对角线长,是第一个公认的无理数,也叫毕达哥拉斯常数,其值到小数点14位约为1.4142135623731。
,它代表边长为1的正方形的对角线长,是第一个公认的无理数,也叫毕达哥拉斯常数,其值到小数点14位约为1.4142135623731。
 是无理数,可由归谬法证明:
是无理数,可由归谬法证明:
- 设
 为有理数,可表示为
为有理数,可表示为 ,其中
,其中 、
、 为互素之正整数。
为互素之正整数。
- 因为
 ,故
,故 是2的倍数,
是2的倍数, 也是2的倍数,记为
也是2的倍数,记为 ,其中
,其中 为正整数。
为正整数。
- 但是
 ,故
,故 ,
, 是2的倍数,
是2的倍数, 也是2的倍数。
也是2的倍数。
- 依上两式,
 、
、 都是2的倍数,和
都是2的倍数,和 、
、 为互素之正整数的前题矛盾。依归谬法,得证
为互素之正整数的前题矛盾。依归谬法,得证 不是有理数,即
不是有理数,即 是无理数。
是无理数。
 。
。
注意,6 的素因数分解为 2 × 3,不能写成某个数的平方,因此  就是最简结果
。
就是最简结果
。
 北宋贾宪增乘开平方法
北宋贾宪增乘开平方法
《九章算术》和《孙子算经》都有筹算的开方法。宋代数学家贾宪发明释锁开平方法、增乘开平方法;明代数学家王素文,程大位发明珠算开平方法,而朱载堉《算学新说》首创用81位算盘开方,精确到25位数字[6]。
长除式算平方根的方式也称为直式开方法,原理是 。
。
- 首先将要开平方根的数从小数点分别向右及向左每两个位一组分开,如98765.432内小数点前的65是一组,87是一组,9是一组,小数点后的43是一组,之后是单独一个2,要补一个0而得20是一组。如1 04.85 73得四组,顺序为1' 04. 85' 73'。
- 将最左的一组的数减去最接近又少于它的平方数,并将该平方数的开方(应该是个位数)记下。
- 将上一步所得之差乘100,和下一组数加起来。
- 将记下的数乘20,然后将它加上某个个位数,再乘以该个个位数,令这个积不大于但最接近上一步所得之差,并将该个个位数记下,且将上一步所得之差减去所得之积。
- 记下的数一次隔两位记下。
- 重复第3步,直到找到答案。
- 可以在数字的最右补上多组的00'以求得理想的精确度为止。
下面以 为例子:
为例子:


四舍五入得答案为14.14。
事实上,将算法稍作改动,可以开任何次方的根,详见n次方算法。
利用高精度长式除法可以计算出1至20的平方根如下:
 |
 |
1
|
 |
 |
1.4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462
|
 |
 |
1.7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909
|
 |
 |
2
|
 |
 |
2.2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638
|
 |
 |
2.4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457
|
 |
 |
2.6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230
|
 |
 |
2.8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924
|
 |
 |
3
|
 |
 |
3.1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639
|
 |
 |
3.3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609
|
 |
 |
3.4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818
|
 |
 |
3.6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293
|
 |
 |
3.7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307
|
 |
 |
3.8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937
|
 |
 |
4
|
 |
 |
4.1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338
|
 |
 |
4.2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386
|
 |
 |
4.3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203
|
 |
 |
4.4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276
|
如果要求 的平方根,选取
的平方根,选取

例子:求 至6位有效数字。
至6位有效数字。






因此 .
.
平方根可以简便地用连分数的形式表示,关于连分数请见连分数,其中1至20的算术平方根分别可用连分数表示为:

![{\displaystyle {\sqrt {2}}=[1;2,2,2,2...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fc9b02798ffa8c81bf9bdcbc2f09e1e0aee4422)
![{\displaystyle {\sqrt {3}}=[1;1,2,1,2...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df0c6eb26d9a8ea8fc7536e85d506c3970d25d3b)

![{\displaystyle {\sqrt {5}}=[2;4,4,4,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3db0b9a3b70d460c26600c2a48038f4044f30bf2)
![{\displaystyle {\sqrt {6}}=[2;2,4,2,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a77c30771fc26826e8d2c5e7bed3f3a41850f47)
![{\displaystyle {\sqrt {7}}=[2;1,1,1,4,1,1,1,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f8ee5f5ca1b5e7fef75103bacd0ffbc18ab597)
![{\displaystyle {\sqrt {8}}=[2;1,4,1,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f94114159ad39146dbee0db04f66f5fc6c5e15ed)

![{\displaystyle {\sqrt {10}}=[3;6,6,6,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/849b4bef93de145e137f648999d6d3c3fab2db5e)
![{\displaystyle {\sqrt {11}}=[3;3,6,3,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf1bddf4ae2a7b8fa8a47e8996cd6f109ddeb0ab)
![{\displaystyle {\sqrt {12}}=[3;2,6,2,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7f86b2454a2b20534e09dbe888b7228db1d8a44)
![{\displaystyle {\sqrt {13}}=[3;1,1,1,1,6,1,1,1,1,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1270c1d403e3d9059ab4cf2c146ecb36c3dc08b0)
![{\displaystyle {\sqrt {14}}=[3;1,2,1,6,1,2,1,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9a7e23c50b6c14119333421f27b7381250c7fe)
![{\displaystyle {\sqrt {15}}=[3;1,6,1,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1883e99932565fc6b8e5a86a3934b130d3cb09be)

![{\displaystyle {\sqrt {17}}=[4;8,8,8,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/099316b44578e9592e1425571402bb24e76664fe)
![{\displaystyle {\sqrt {18}}=[4;4,8,4,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4a789b740adf75a585e1a4e3bb5d85a2fc23056)
![{\displaystyle {\sqrt {19}}=[4;2,1,3,1,2,8,2,1,3,1,2,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7cd3c48024a8f78a4b7ce606d442893d273e665)
![{\displaystyle {\sqrt {20}}=[4;2,8,2,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8ab7596515455a8476ccbcd6827283d0eab5ed0)
连分数部分均循环,省略号前为2或4个循环节。
巴比伦求平方根的算法实际上很简单:(假设要求一个数N的平方根)
- 预测一个平方根
 ,初始另一个值
,初始另一个值 ,且
,且
- 求预测值与初始值的均值:
 ,
, 
- 比较
 和
和 的差值是否达到精度,如果无,继续步骤
的差值是否达到精度,如果无,继续步骤
这个方法是从佩尔方程演变过来的,它通过不断减去奇数来求得答案。
给定线段AB和1,求一条长为 的线段。
的线段。
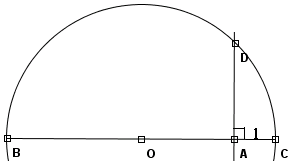
- 画线AB,延长BA至C使

- 以BC的中点为圆心,OC为半径画圆
- 过A画BC的垂直线,垂直线和圆弧交于D,AD即为所求之长度
将整个过程搬到直角座标上,已知AC=1,设
- O=

- AB=

- 直径为BC的圆就是
 (圆的方程式:
(圆的方程式: )(其中
)(其中 表示半径。)
表示半径。)
- 将
 (A,D所在的x座标)代入上面的方程式
(A,D所在的x座标)代入上面的方程式

- 解方程,得
 。
。
另也可参见射影定理。
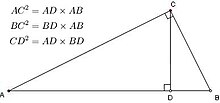 射影定理(图)
射影定理(图)
- ^ Analysis of YBC 7289. ubc.ca. [19 January 2015]. (原始内容存档于2020-03-12).
- ^ Anglin, W.S. (1994). Mathematics: A Concise History and Philosophy. New York: Springer-Verlag.
- ^ Heath, Sir Thomas L. The Thirteen Books of The Elements, Vol. 3. Cambridge University Press. 1908: 3.
- ^ Abramowitz, Milton; Stegun, Irene A. Handbook of mathematical functions with formulas, graphs, and mathematical tables. Courier Dover Publications. 1964: 17. ISBN 0-486-61272-4. (原始内容存档于2016-04-23). , Section 3.7.27, p. 17 互联网档案馆的存档,存档日期2009-09-10.
- ^ Cooke, Roger. Classical algebra: its nature, origins, and uses. John Wiley and Sons. 2008: 59. ISBN 0-470-25952-3. (原始内容存档于2016-04-23).
- ^ 劳汉生《珠算与实用算术》ISBN 7-5375-1891-2/O



















![{\displaystyle {\sqrt[{n}]{\,\,}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddcb8a480722f2e988fb8ebe5dfd905140a9a52a)
























![{\displaystyle {\begin{aligned}{\sqrt {i}}&=\left[\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)\right]^{\frac {1}{2}}\\&=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)\\&={\frac {\sqrt {2}}{2}}+i{\frac {\sqrt {2}}{2}}\\&={\frac {\sqrt {2}}{2}}(1+i)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f86b3b7203a50d96454199f6b6b0ca30d029303)






































































![{\displaystyle {\sqrt {2}}=[1;2,2,2,2...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fc9b02798ffa8c81bf9bdcbc2f09e1e0aee4422)
![{\displaystyle {\sqrt {3}}=[1;1,2,1,2...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df0c6eb26d9a8ea8fc7536e85d506c3970d25d3b)

![{\displaystyle {\sqrt {5}}=[2;4,4,4,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3db0b9a3b70d460c26600c2a48038f4044f30bf2)
![{\displaystyle {\sqrt {6}}=[2;2,4,2,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a77c30771fc26826e8d2c5e7bed3f3a41850f47)
![{\displaystyle {\sqrt {7}}=[2;1,1,1,4,1,1,1,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f8ee5f5ca1b5e7fef75103bacd0ffbc18ab597)
![{\displaystyle {\sqrt {8}}=[2;1,4,1,4...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f94114159ad39146dbee0db04f66f5fc6c5e15ed)
![{\displaystyle {\sqrt {10}}=[3;6,6,6,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/849b4bef93de145e137f648999d6d3c3fab2db5e)
![{\displaystyle {\sqrt {11}}=[3;3,6,3,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf1bddf4ae2a7b8fa8a47e8996cd6f109ddeb0ab)
![{\displaystyle {\sqrt {12}}=[3;2,6,2,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7f86b2454a2b20534e09dbe888b7228db1d8a44)
![{\displaystyle {\sqrt {13}}=[3;1,1,1,1,6,1,1,1,1,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1270c1d403e3d9059ab4cf2c146ecb36c3dc08b0)
![{\displaystyle {\sqrt {14}}=[3;1,2,1,6,1,2,1,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9a7e23c50b6c14119333421f27b7381250c7fe)
![{\displaystyle {\sqrt {15}}=[3;1,6,1,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1883e99932565fc6b8e5a86a3934b130d3cb09be)

![{\displaystyle {\sqrt {17}}=[4;8,8,8,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/099316b44578e9592e1425571402bb24e76664fe)
![{\displaystyle {\sqrt {18}}=[4;4,8,4,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4a789b740adf75a585e1a4e3bb5d85a2fc23056)
![{\displaystyle {\sqrt {19}}=[4;2,1,3,1,2,8,2,1,3,1,2,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7cd3c48024a8f78a4b7ce606d442893d273e665)
![{\displaystyle {\sqrt {20}}=[4;2,8,2,8...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8ab7596515455a8476ccbcd6827283d0eab5ed0)












