Β分布|
機率密度函數  |
|
累積分布函數 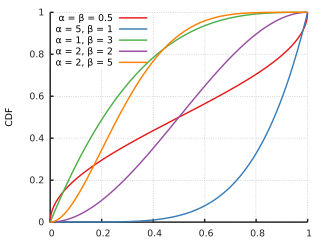 |
| 母數 |

 |
|---|
| 值域 |
 |
|---|
| 機率密度函數 |
 |
|---|
| 累積分布函數 |
 |
|---|
| 期望值 |
![{\displaystyle \operatorname {E} [x]={\frac {\alpha }{\alpha +\beta }}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0569ee58528ca526f9cdab57675a2d0d73bf4766)
![{\displaystyle \operatorname {E} [\ln x]=\psi (\alpha )-\psi (\alpha +\beta )\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a2d06fc2308f395e3dbaed6bb7d0b975d38eb1)
(見雙伽瑪函數) |
|---|
| 中位數 |
 無解析表達 無解析表達 |
|---|
| 眾數 |
 for for  |
|---|
| 變異數 |
 |
|---|
| 偏度 |
 |
|---|
| 峰度 |
見文字 |
|---|
| 熵 |
見文字 |
|---|
| 動差母函數 |
 |
|---|
| 特徵函數 |
 (見合流超幾何函數) (見合流超幾何函數) |
|---|
Β分布,亦稱貝它分布、Beta 分布(Beta distribution),在機率論中,是指一組定義在 區間的連續機率分布,有兩個母數
區間的連續機率分布,有兩個母數 。
。
Β分布的機率密度函數是:
![{\displaystyle {\begin{aligned}f(x;\alpha ,\beta )&={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\int _{0}^{1}u^{\alpha -1}(1-u)^{\beta -1}\,du}}\\[6pt]&={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\\[6pt]&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/835449e193daf41f7721dec385b81fb4a16375b2)
其中 是Γ函數。如果
是Γ函數。如果 為正整數,則有:
為正整數,則有:

隨機變數X服從母數為 的Β分布通常寫作
的Β分布通常寫作

Β分布的累積分布函數是:

其中 是不完全Β函數,
是不完全Β函數, 是正則不完全貝塔函數。
是正則不完全貝塔函數。
母數為 Β分布的眾數是:
Β分布的眾數是:
 [1]
[1]
期望值和變異數分別是:


偏度是:
![{\displaystyle {\frac {\operatorname {E} (X-\mu )^{3}}{[\operatorname {E} (X-\mu )^{2}]^{3/2}}}={\frac {2(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d12bd747cbf5cc3410db8103716da3f202eff5b7)
峰度是:
![{\displaystyle {\frac {\operatorname {E} (X-\mu )^{4}}{[\operatorname {E} (X-\mu )^{2}]^{2}}}-3={\frac {6[\alpha ^{3}-\alpha ^{2}(2\beta -1)+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e70dc91216082cdf757ded4e3ab81c15418d8cb2)
或:
![{\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea65a8d7c9e00ba6299b727eab679117776f41e)
 階動差是:
階動差是:

其中 表示遞進階乘冪。
表示遞進階乘冪。 階動差還可以遞迴地表示為:
階動差還可以遞迴地表示為:

另外,

給定兩個Β分布隨機變數, X ~ Beta(α, β) and Y ~ Beta(α', β'), X的微分熵為:[2]

其中 表示雙伽瑪函數。
表示雙伽瑪函數。
聯合熵為:

其KL散度為:

- ^ Johnson, Norman L., Samuel Kotz, and N. Balakrishnan (1995). "Continuous Univariate Distributions, Vol. 2", Wiley, ISBN 978-0-471-58494-0.
- ^ A. C. G. Verdugo Lazo and P. N. Rathie. "On the entropy of continuous probability distributions," IEEE Trans. Inf. Theory, IT-24:120–122,1978.








![{\displaystyle \operatorname {E} [x]={\frac {\alpha }{\alpha +\beta }}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0569ee58528ca526f9cdab57675a2d0d73bf4766)
![{\displaystyle \operatorname {E} [\ln x]=\psi (\alpha )-\psi (\alpha +\beta )\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a2d06fc2308f395e3dbaed6bb7d0b975d38eb1)









![{\displaystyle {\begin{aligned}f(x;\alpha ,\beta )&={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\int _{0}^{1}u^{\alpha -1}(1-u)^{\beta -1}\,du}}\\[6pt]&={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\\[6pt]&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/835449e193daf41f7721dec385b81fb4a16375b2)











![{\displaystyle {\frac {\operatorname {E} (X-\mu )^{3}}{[\operatorname {E} (X-\mu )^{2}]^{3/2}}}={\frac {2(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d12bd747cbf5cc3410db8103716da3f202eff5b7)
![{\displaystyle {\frac {\operatorname {E} (X-\mu )^{4}}{[\operatorname {E} (X-\mu )^{2}]^{2}}}-3={\frac {6[\alpha ^{3}-\alpha ^{2}(2\beta -1)+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e70dc91216082cdf757ded4e3ab81c15418d8cb2)
![{\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea65a8d7c9e00ba6299b727eab679117776f41e)