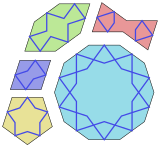
十角星
外观
| 正十角星 | |
|---|---|
 正十角星形 | |
| 对偶 | 自身对偶 |
| 边 | 10 |
| 顶点 | 10 |
| 施莱夫利符号 | 10/3 5/3 |
| 考克斯特符号 | |
| 鲍尔斯缩写 | deg |
| 对称群 | 二面体群 (D10) |
| 内角(度) | 72 |
| 特性 | 星形、外接圆、等边、等角、isotoxal |
十角星,又称十芒星,是指一种有十只尖角,并以十条直线画成的星星图形。
几何学
[编辑]在几何学中,十角星是边自我相交的十边形。
正十角星只有一种,其施莱夫利符号为{10/3},与所述第二数字差别在绘制十角星时顶点间隔数。[1]
正十角星每边为,正十角星各边的长度比例,以及在每个边的交叉点比例在以下图形所示。

在几何学上,只要拥有10个边、10个角,并可用10边形容纳的图形即可称为十角星,其符号以{10/n}表示。只有{10/3}的十角星为正十角星,但还有三种十角星也可被解释为正十角星。
| 形式 | 多边形 | 复合多边形 | 星形多边形 | 复合多边形 | |
|---|---|---|---|---|---|
| 图形 | 
|

|

|

|
|
| 符号 | {10/1} = {10} | {10/2} = 2{5} | {10/3} | {10/4} = 2{5/2} | {10/5} = 5{2} |
与五角星及五边形相关性
[编辑]十角星与五角星及五边形有一定的关连性,当五角星或五边形截断边角时,也可创造出十角星。[4][5][6]
以下列表列出十角星与五角星及五边形的关连性。
| 拟正多面体 | 等角多边形 | 拟正多面体 双层覆盖形式 | |
|---|---|---|---|
 t{5} = {10} |
|

|
 t{5/4} = {10/4} = 2{5/2} |
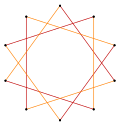 t{5/3} = {10/3} |

|
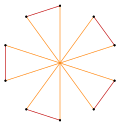
|
 t{5/2} = {10/2} = 2{5} |
应用
[编辑]参见
[编辑]参考文献
[编辑]- ^ Barnes, John, Gems of Geometry, Springer: 28–29, 2012 [2015-08-16], ISBN 9783642309649, (原始内容存档于2019-06-08).
- ^ Regular polytopes, p 93-95, regular star polygons, regular star compounds
- ^ Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons p.36-38
- ^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Grünbaum, B..
- ^ *Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. Uniform polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society). 1954, 246 (916): 411. ISSN 0080-4614. JSTOR 91532. MR 0062446. doi:10.1098/rsta.1954.0003.
- ^ Coxeter, The Densities of the Regular polytopes I, p.43 If d is odd, the truncation of the polygon {p/q} is naturally {2n/d}. But if not, it consists of two coincident {n/(d/2)}'s; two, because each side arises from an original side and once from an original vertex. Thus the density of a polygon is unaltered by truncation.
- ^ Sarhangi, Reza, Polyhedral Modularity in a Special Class of Decagram Based Interlocking Star Polygons, Bridges 2012: Mathematics, Music, Art, Architecture, Culture (PDF): 165–174, 2012 [2015-08-16], (原始内容 (PDF)存档于2015-02-05).