在機率論與統計學中,任意隨機變數的對數服從常態分布,則這個隨機變數服從的分布稱為對數常態分布。如果  是常態分布的隨機變數,則
是常態分布的隨機變數,則  (指數函數)為對數常態分布;同樣,如果
(指數函數)為對數常態分布;同樣,如果  是對數常態分布,則
是對數常態分布,則  為常態分布。
如果一個變量可以看作是許多很小獨立因子的乘積,則這個變量可以看作是對數常態分布。一個典型的例子是股票投資的長期收益率,它可以看作是每天收益率的乘積。
對於
為常態分布。
如果一個變量可以看作是許多很小獨立因子的乘積,則這個變量可以看作是對數常態分布。一個典型的例子是股票投資的長期收益率,它可以看作是每天收益率的乘積。
對於  ,對數常態分布的機率密度函數為
,對數常態分布的機率密度函數為

其中  與
與  分別是變量對數的平均值與標準差。它的期望值是
分別是變量對數的平均值與標準差。它的期望值是

變異數為

給定期望值與變異數,也可以用這個關係求  與
與 


對數常態分布、幾何平均數與幾何標準差是相互關聯的。在這種情況下,幾何平均值等於  ,幾何標準差等於
,幾何標準差等於  。
。
如果採樣數據來自於對數常態分布,則幾何平均值與幾何標準差可以用於估計信賴區間,就像用算術平均數與標準差估計常態分布的信賴區間一樣。
| 信賴區間界
|
對數空間
|
幾何
|
| 3σ 下界
|

|

|
| 2σ 下界
|

|

|
| 1σ 下界
|

|

|
| 1σ 上界
|

|

|
| 2σ 上界
|

|

|
| 3σ 上界
|

|

|
其中幾何平均數  ,幾何標準差
,幾何標準差 
原始動差為:




或者更為一般的動差

隨機變數  在閾值
在閾值  上的局部期望值定義為
上的局部期望值定義為

其中  是機率密度。對於對數常態機率密度,這個定義可以表示為
是機率密度。對於對數常態機率密度,這個定義可以表示為

其中  是標準常態部分的累積分布函數。對數常態分布的局部期望值在保險業及經濟領域都有應用,著名的Black-Scholes期權定價公式便可由此推導出。
是標準常態部分的累積分布函數。對數常態分布的局部期望值在保險業及經濟領域都有應用,著名的Black-Scholes期權定價公式便可由此推導出。
為了確定對數常態分布母數  與
與  的最大概似估計,我們可以採用與常態分布母數最大概似估計同樣的方法。我們來看
的最大概似估計,我們可以採用與常態分布母數最大概似估計同樣的方法。我們來看

其中用  表示對數常態分布的機率密度函數,用
表示對數常態分布的機率密度函數,用  — 表示常態分布。因此,用與常態分布同樣的指數,我們可以得到對數最大概似函數:
— 表示常態分布。因此,用與常態分布同樣的指數,我們可以得到對數最大概似函數:

由於第一項相對於  與
與  來說是常數,兩個對數最大概似函數
來說是常數,兩個對數最大概似函數  與
與  在同樣的
在同樣的  與
與  處有最大值。因此,根據常態分布最大概似母數估計器的公式以及上面的方程式,我們可以推導出對數常態分布母數的最大概似估計
處有最大值。因此,根據常態分布最大概似母數估計器的公式以及上面的方程式,我們可以推導出對數常態分布母數的最大概似估計

- 如果
 與
與  ,則
,則  是常態分布。
是常態分布。
- 如果
 是有同樣
是有同樣  母數、而
母數、而  可能不同的統計獨立對數常態分布變量 ,並且
可能不同的統計獨立對數常態分布變量 ,並且  ,則
,則  也是對數常態分布變量:
也是對數常態分布變量: 。
。
- 對數常態分布, Aitchison, J. and Brown, J.A.C. (1957)
- Log-normal Distributions across the Sciences: Keys and Clues (頁面存檔備份,存於網際網路檔案館), E. Limpert, W. Stahel and M. Abbt,. BioScience, 51 (5), p. 341–352 (2001).
- 對數常態分布特性, John Hull, in Options, Futures, and Other Derivatives 6E (2005). ISBN 0-13-149908-4
- Eric W. Weisstein et al. 對數常態分布 (頁面存檔備份,存於網際網路檔案館) at MathWorld. Electronic document, 2006年10月26日造訪.





![{\displaystyle {\frac {1}{x\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {\left[\ln(x)-\mu \right]^{2}}{2\sigma ^{2}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e605155f0b7a0b12d504d34eea75b858cf26cb75)
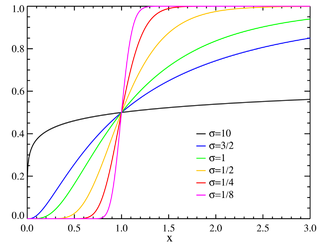
![{\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7994d3788092e1e39ed152b0f37c9626b8a32f0)




























































