等腰三角形
外观
| 等腰三角形 | |
|---|---|
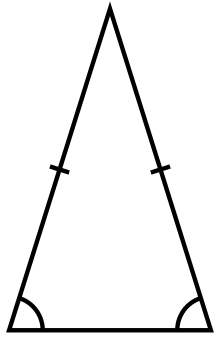 等腰三角形 | |
| 对偶 | 相似的等腰三角形 |
| 边 | 3 |
| 顶点 | 3 |
| 施莱夫利符号 | {3} (底角和顶角相等) |
| 鲍尔斯缩写 | isot |
| 面积 | 或
|
| 内角(度) | 60° (底角和顶角相等时)
|
在几何学中,等腰三角形(英语:Isosceles triangle)是指至少有两边长度相等的三角形,因此会造成有2个角相等。相等的两个边称等腰三角形的腰,另一边称为底边,相等的两个角称为等腰三角形的底角,其余的角叫做顶角。[1]
等腰三角形的重心、和垂心都位于顶点向底边的垂线,可以把等腰三角形分成两个全等的直角三角形。[2]
等边三角形是底边和腰等长的等腰三角形,是等腰三角形的一个特殊形式。若等腰三角形的顶角为直角,称为等腰直角三角形。
命名
[编辑]等腰三角形在英文中称为isosceles,来自希腊文,意思是“等长的脚”[2]
性质
[编辑]等腰三角形具有下列性质[1]:P.204:
- 两底角相等
- 顶角的角平分线、底边的中线和高互相重合
- 当腰长等于底边长时,则底角和顶角为60度(即等边三角形)
| 边长 |
|
|---|---|
| 角 | |
| 面积 | 或 |
| 周长 |
等腰三角形定理
[编辑]若一三角形的二边相等,则二边的对角相等,此定理列在欧几里德的《几何原本》中,称为驴桥定理,也是等腰三角形定理。驴桥定理是在几何原本的前面出现的较困难命题,是数学能力的一个门槛[3],无法理解此一命题的人可能也无法处理后面更难的命题。
驴桥定理的逆定理是若一三角形的二角相等,则二角的对边相等。
等腰三角形的全等
[编辑]若二等腰三角形,其腰相等,底边也相等,即可以用SSS全等证明二个等腰三角形全等,而三角形的角可以用余弦定理求得。
等腰三角形的相似
[编辑]等腰三角形的顶角 和底角有以下的关系:
已知其中一个就可以知道另一个,若二等腰三角形的顶角相等或底角相等,即可以用AAA相似证明二个等腰三角形全等,各边的关系可以用正弦定理求得。
对称轴
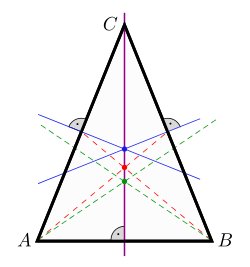
[编辑]等腰三角形为轴对称,其对称轴和底边的高、中垂线、中线及顶角的角平分线重合(三线合一)[4]。等腰三角形的内心、外心、重心、垂心及顶点所对旁心五心共线,都在对称轴上[5]。
|
等腰三角形
|
和其他图形的关系
[编辑]- 二个底边相等的等腰三角形可以组合成一个筝形,此筝形有一个对称轴,即为二等腰三角形的高。
- 二个全等的等腰三角形可以组合成一个菱形,此菱形有二个对称轴,包括二等腰三角形的高,以及等腰三角形的底边。
- 圆锥的投影图中有一面即为等腰三角形。
- 将扇形的二半径和扇形的弦相连,也是等腰三角形。
相关条目
[编辑]参考文献
[编辑]- ^ 1.0 1.1 《中学数学实用辞典》ISBN 957-603-093-5 九章出版.
- ^ 2.0 2.1 《图解数学辞典》天下远见出版 P.37 三角形 ISBN 986-417-614-5
- ^ 吴任哲. 利用『驢橋定理』探討國中教師之數學教學. HPM通讯第四卷8,9期合刊. [2013-08-21]. (原始内容存档于2013-08-04).
- ^ 云南教育编辑部. 云南教育. 云南省教育厅. 1991 [2013-08-22]. (原始内容存档于2019-05-03).
- ^ 何思谦. 数学辞海. 山西敎育出版社. 2002 [2013-08-22]. (原始内容存档于2021-01-08).














