超無限邊形
| 偽多邊形 超無限邊形 | |
|---|---|
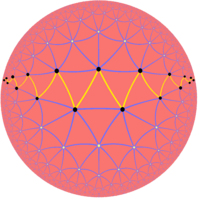
 超無限邊形（Pseudogon） 雙曲正無限邊形 雙曲面上的超無限邊形。 | |
| 類型 | 正多邊形 二維雙曲鑲嵌 |
| 對偶 | 自身對偶 |
| 邊 | iπ/λ ∞ |
| 頂點 | iπ/λ ∞ |
| 施萊夫利符號 | {iπ/λ} {∞} |
| 考克斯特符號 |    |
| 對稱群 | [iπ/λ] |
| 內角（度） | 雙曲平角 |
| 特性 | 非嚴格凸, 圓內接多邊形, 等邊多邊形, 等角多邊形, 雙曲線, 發散 |
在幾何學中，偽多邊形（英語：pseudogon）又稱為超無限邊形，是一種位於雙曲平面上的無限邊形，具有超無限邊形群（pseudogonal group）的對稱性，諾曼·約翰遜將一般的發散鏡射形式的無限邊形稱為超無限邊形，其外接圓為極限圓，正超無限邊形在施萊夫利符號中用{iπ/λ}表示，其中λ表示發散垂直鏡射的週期距離[1]，用來表示其拓撲結構具有比無限邊形更多的邊與頂點，換句話說，若其不為發散鏡射形式則只能看做為普通的無限邊形，也因此超無限邊形無法在平面上存在。此外，偽多邊形也可以解釋為未完全具備多邊形性質的多邊形[2]，此種情況下未必需要位於雙曲面，這種偽多邊形其英文也可以寫為pseudo polygon[3][4]。
正超無限邊形
[編輯]
正超無限邊形（英語：regular pseudogon）又稱雙曲正無限邊形，是雙曲線H1（並非歐幾里得線）分割為每段長度為2λ線段形成的無限邊形，為具有[iπ/λ]考克斯特群的羅氏無限邊形，可以視為正無限邊形的一種類似物。[5]依據其考克斯特群，其邊數和頂點數將會是iπ/λ個，事實上它頂點數為正無窮大，邊長為2λ，其中iπ/λ用來表示超平形（ultraparallel）的鏡射，虛數值使鏡射變換的角度以一個雙曲線的形式，而存在等式cos(π/n) = cos(πλ/(iπ)) = cosh(2λ)，而λ∈{ π/n | n∈Z }。
其亦可以視為二維空間的雙曲密鋪，和三維雙曲密鋪如：正七邊形鑲嵌、七階三角形鑲嵌等，做類比[6]。其屬於非緊湊空間。
正超無限邊形無法在平面上存在，但可以構造在雙曲面。其可以擁有外接圓和內切圓，但他們必須是雙曲超圓形。
扭歪超無限邊形
[編輯]扭歪超無限邊形（英語：Skew pseudogon）是超無限邊形對應的扭歪多邊形，即位於非緊雙曲空間的雙曲扭歪無限邊形。
|
| 圍繞着超無限邊形的三角形也可以構造出等邊扭歪超無限邊形 |
| {3,7}的皮特里多邊形 | t{3,7}的皮特里多邊形 |
|---|---|
 正扭歪 |
 半正扭歪 |
鑲嵌與密鋪
[編輯]正超無限邊形不能構成平面鑲嵌，但可以構成雙曲鑲嵌，如三階超無限邊形鑲嵌，其考克斯特記號計為
。該鑲嵌可以視為超無限邊形在三維空間的類比，稱為偽多面體（pseudohedron）。
二個超無限邊形即可完全鑲嵌整個雙曲平面，稱為二階超無限邊形鑲嵌。
| 正 | 半正 | ||
|---|---|---|---|
| ∞.∞ | 2∞ | 4.4.∞ | 3.3.3.∞ |
|
|
|
|
{iπ/λ, 2}
|
{2, iπ/λ}
|
t{2, iπ/λ}
|
sr{2, iπ/λ} 
|
| 對稱群：[iπ/λ,iπ/λ], (*iπ/λ iπ/λ 2) | [iπ/λ,iπ/λ]+, (iπ/λ iπ/λ 2) | ||||||
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| {9i,9i} 超無限階 超無限邊形鑲嵌 |
t{9i,9i} 截角超無限階 超無限邊形鑲嵌 |
r{9i,9i} 截半超無限階 超無限邊形鑲嵌 |
2t{9i,9i}=t{9i,9i} 截角超無限階 超無限邊形鑲嵌 |
2r{9i,9i}={9i,9i} 超無限階 超無限邊形鑲嵌 |
rr{9i,9i} 小斜方截半 超無限階 超無限邊形鑲嵌 |
tr{9i,9i} 大斜方截半 超無限階 超無限邊形鑲嵌 |
sr{9i,9i} 扭稜超無限階 超無限邊形鑲嵌 |
| 對稱群：[iπ/λ,3], (*∞32) | [iπ/λ,3]+ (∞32) |
[1+,iπ/λ,3] (*∞33) |
[iπ/λ,3+] (3*∞) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 考克斯特記號 |
|
|
|
|
|
|
|
|
|
|
|
 =  
|
=
|
= 
|
|
= or 
|
= or
|
= 
| |||||
| 圖像 | 
|
|
|
|
|
|
|
||||
| 頂點圖 | ∞.∞.∞ | 3.∞.∞ | 3.∞.3.∞ | ∞.6.6 | 3∞ | 3.4.∞.4 | 4.6.∞ | 3.3.3.3.∞ | 3.∞.3.∞.3.∞ | ||
| 類比 | {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | h2{∞,3} | s{3,∞} |
| 半正對偶 | |||||||||||
| 考克斯特記號 | 
|
|
|
|
|
|
|
|
|
| |
| 圖像 |
|
|
|
|
|
|
|
||||
| 頂點佈局 類比 |
V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
高維類比
[編輯]
偽多面體（pseudohedron）是超無限邊形在三維空間的類比，即在三維非緊雙曲空間中的無限面體，又稱為超無限面體。例如三階七邊形鑲嵌蜂巢體中的正七邊形鑲嵌，由於要使每個頂點都是3個正七邊形鑲嵌的公共頂點使得圖形被變換到非緊雙曲空間中，即幾何中心跑到龐加萊模型外，其外接球為三維雙曲極限球。
超無限胞體（pseudotope）則為非緊雙曲鑲嵌在四維或更高維度類比，例如四階一百二十胞體堆砌[8]。
但嚴格來說，偽多胞形（pseudotope）只會在二維雙曲空間討論，由於二維的考克斯特群表達到無窮之後仍為平面，因此只能用雙曲鏡射的方式以虛數表達雙曲幾何圖形。
| 群 | 赫爾曼莫金記號 | 軌道流形 | 考克斯特 | 考克斯特圖 | 階 |
|---|---|---|---|---|---|
| 有限 | |||||
| Zn | n | n• | [n]+ |  
|
n |
| Dn | nm | *n• | [n] |
|
2n |
| 仿射 | |||||
| Z∞ | ∞ | ∞• | [∞]+ | 
|
∞ |
| Dih∞ | ∞m | *∞• | [∞] |
|
∞ |
| 雙曲 | |||||
| Z∞ | [πi/λ]+ |
|
∞ | ||
| Dih∞ | [πi/λ] |
|
∞ | ||
參見
[編輯]參考文獻
[編輯]- ^ Johnson, Norman W. 11.2 The polygonal groups. Geometries and transformations. Cambridge University Press. 2018: 141.
- ^ HSKR, K. L. Dr. cjl. 1989. PhD Thesis. SIMON FRASER UNIVERSITY.
- ^ 台北盆地聚落發展之空間分析 （頁面存檔備份，存於互聯網檔案館） 國立台灣大學地理環境資源學系暨研究所 2005-10-31
- ^ 中學地理科常用英漢辭彙 （頁面存檔備份，存於互聯網檔案館） 香港教育局
- ^ Johnson, Norman W. 11: Finite Symmetry Groups. Geometries and transformations. Cambridge University Press. 2018: 226 [2022-05-30]. （原始內容存檔於2022-08-03）.
- ^ Coxeter, H. S. M. Regular Polytopes 3rd ed. New York: Dover Publications. 1973: 121–122. ISBN 0-486-61480-8. p.296, Table II: Regular honeycombs
- ^ John Baez, Visual insights: {7,3,3} Honeycomb （頁面存檔備份，存於互聯網檔案館） (2014/08/01)
- ^ Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V, p212-213)