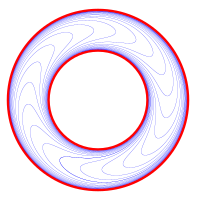
里布葉狀結構 的2維截面里布葉狀結構的3維模型 微分幾何 中,葉狀結構 (foliation )是n -流形等價關係 ,等價類 是連通單射 浸入子流形 ,都具有相同維度p ,以實坐標空間
R
n
{\displaystyle \mathbb {R} ^{n}}
分解 為標準嵌入 子空間
R
p
{\displaystyle \mathbb {R} ^{p}}
陪集
x
+
R
p
{\displaystyle x+\mathbb {R} ^{p}}
葉 (leaf)。[ 1]
C
r
{\displaystyle C^{r}}
分段線性 、微分 或解析 結構,就可分別定義分段線性、微分、解析葉狀結構。在最重要的
C
r
{\displaystyle C^{r}}
r ≥ 1(否則
C
0
{\displaystyle C^{0}}
[ 2] p (葉的維度)稱作葉狀結構的維度,
q
=
n
−
p
{\displaystyle q=n-p}
余維數 。
在數學物理學家關於廣義相對論 的一些論文中,「葉狀結構」用於描述:相關的洛倫茲流形 ((p +1)維時空 )分解為p 維超平面 ,指定為梯度 處處不為零的實值光滑函數 (純量場 )的水平集;這光滑函數通常被假定為時間函數 ,梯度處處類時間 ,因此其水平集都是類空間超平面。為與標準數學術語保持一致,這些超平面通常稱作葉狀結構的葉。[ 3] 局部 上總是函數的水平集,但一般不能在全局這樣表達,[ 4] [ 5] 完整 也可能阻礙葉的全局一致定義函數的存在。例如,雖然3-球面 有一個由里布發現的余維1-葉狀結構,但閉流形的余維-1葉狀結構不能由光滑函數的水平集給出,因為閉流形上的光滑函數必然在最值點有臨界點。
葉狀結構好比是一種給流形 穿的條紋織物的衣服。在流形的每個足夠小的片上,這些條紋給了流形一個局部乘積結構,不需在局部區域之外一致(不用有良定義 的整體結構):沿着一個條紋走足夠遠,可能回到不同的鄰近的條紋。
為給葉狀結構下精確定義,需先定義一些輔助元素。
3維葉狀圖(foliated chart),n = 3、q = 1。斑(plaque)是2維的,橫截(transversal)是1維的。
R
n
{\displaystyle \mathbb {R} ^{n}}
矩鄰域 是形式為
B
=
J
1
×
⋯
×
J
n
{\displaystyle B=J_{1}\times \cdots \times J_{n}}
開 子集 ,其中
J
i
{\displaystyle J_{i}}
i 個坐標軸上(可能無界)的相對開區間。若
J
1
{\displaystyle J_{1}}
(
a
,
0
]
{\displaystyle (a,\ 0]}
B 具有邊界 [ 6]
∂
B
=
{
(
0
,
x
2
,
…
,
x
n
)
∈
B
}
.
{\displaystyle \partial B=\left\{\left(0,x^{2},\ldots ,x^{n}\right)\in B\right\}.}
在下面的定義中,坐標圖(coordinate chart)被認為是在
R
p
×
R
q
{\displaystyle \mathbb {R} ^{p}\times \mathbb {R} ^{q}}
凸 )角的可能。
n -流形M 上余維為q 的葉狀圖(foliated chart)是
(
U
,
φ
)
{\displaystyle (U,\ \varphi )}
U
⊂
M
{\displaystyle U\subset M}
φ
:
U
→
B
τ
×
B
⋔
{\displaystyle \varphi :U\to B_{\tau }\times B_{\pitchfork }}
微分同胚 ,
B
⋔
{\displaystyle B_{\pitchfork }}
R
q
{\displaystyle \mathbb {R} ^{q}}
B
τ
{\displaystyle B_{\tau }}
R
p
{\displaystyle \mathbb {R} ^{p}}
P
y
=
φ
−
1
(
B
τ
×
{
y
}
)
{\displaystyle P_{y}=\varphi ^{-1}(B_{\tau }\times \{y\})}
y
∈
B
⋔
{\displaystyle y\in B_{\pitchfork }}
∀
x
∈
B
τ
{\displaystyle \forall x\in B_{\tau }}
S
x
=
φ
x
=
φ
−
1
(
{
x
}
×
B
⋔
)
{\displaystyle S_{x}=\varphi _{x}=\varphi ^{-1}(\{x\}\times B_{\pitchfork })}
橫截 (transversal)。集合
∂
τ
U
=
φ
−
1
(
B
τ
×
(
∂
B
⋔
)
)
{\displaystyle \partial _{\tau }U=\varphi ^{-1}(B_{\tau }\times (\partial B_{\pitchfork }))}
U 的切邊界(tangential boundary),
∂
⋔
U
=
φ
−
1
(
(
∂
B
τ
)
×
B
⋔
)
{\displaystyle \partial _{\pitchfork }U=\varphi ^{-1}((\partial B_{\tau })\times B_{\pitchfork })}
U 的橫截邊界(transverse boundary)。[ 7]
葉狀圖是所有葉狀結構的基本模型,斑就是葉。
B
τ
{\displaystyle B_{\tau }}
B -切」,
B
⋔
{\displaystyle B_{\pitchfork }}
B -截」。還有多種可能。若
B
⋔
,
B
τ
{\displaystyle B_{\pitchfork },\ B_{\tau }}
n -流形的余維-q 葉狀結構。若其中一個矩鄰域有界,則葉狀圖建模了有界無角n -流形的葉狀結構的各種可能性。具體來說,若
∂
B
⋔
≠
∅
=
∂
B
τ
{\displaystyle \partial B_{\pitchfork }\neq \varnothing =\partial B_{\tau }}
∂
U
=
∂
τ
U
{\displaystyle \partial U=\partial _{\tau }U}
∂
B
τ
≠
∅
=
∂
B
⋔
{\displaystyle \partial B_{\tau }\neq \varnothing =\partial B_{\pitchfork }}
∂
U
=
∂
⋔
U
{\displaystyle \partial U=\partial _{\pitchfork }U}
∂
B
⋔
≠
∅
≠
∂
B
τ
{\displaystyle \partial B_{\pitchfork }\neq \varnothing \neq \partial B_{\tau }}
[ 7]
(a ) 與邊界相切的葉狀結構
∂
B
⋔
≠
∅
=
∂
B
τ
{\displaystyle \partial B_{\pitchfork }\neq \varnothing =\partial B_{\tau }}
b ) 與邊界相截的葉狀結構
∂
B
τ
≠
∅
=
∂
B
⋔
{\displaystyle \partial B_{\tau }\neq \varnothing =\partial B_{\pitchfork }}
c ) 角將切邊界與橫截邊界隔開的葉狀結構
∂
B
⋔
≠
∅
≠
∂
B
τ
{\displaystyle \partial B_{\pitchfork }\neq \varnothing \neq \partial B_{\tau }}
n -流形M 上余維為q 的
C
r
(
0
≤
r
≤
∞
)
{\displaystyle C^{r}\ (0\leq r\leq \infty )}
葉狀圖冊 (foliated atlas)是余維為q 的葉狀圖的
C
r
{\displaystyle C^{r}}
U
=
{
(
U
α
,
φ
α
)
∣
α
∈
A
}
{\displaystyle {\mathcal {U}}=\{(U_{\alpha },\varphi _{\alpha })\mid \alpha \in A\}}
P 、Q 在
U
{\displaystyle {\mathcal {U}}}
P ∩ Q 在P 、Q 中都是開的,它們就是相干葉狀結構(coherently foliated)。[ 8]
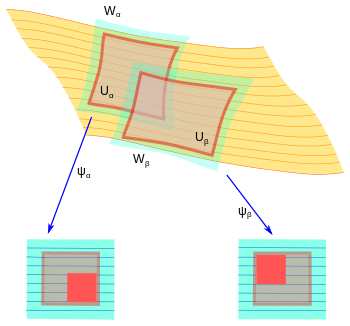
重新表述相干葉狀圖的有效方法是將
w
∈
U
α
∩
U
β
{\displaystyle w\in U_{\alpha }\cap U_{\beta }}
[ 9]
φ
α
(
w
)
=
(
x
α
(
w
)
,
y
α
(
w
)
)
∈
B
τ
α
×
B
⋔
α
,
{\displaystyle \varphi _{\alpha }(w)=\left(x_{\alpha }(w),y_{\alpha }(w)\right)\in B_{\tau }^{\alpha }\times B_{\pitchfork }^{\alpha },}
φ
β
(
w
)
=
(
x
β
(
w
)
,
y
β
(
w
)
)
∈
B
τ
β
×
B
⋔
β
.
{\displaystyle \varphi _{\beta }(w)=\left(x_{\beta }(w),y_{\beta }(w)\right)\in B_{\tau }^{\beta }\times B_{\pitchfork }^{\beta }.}
(
U
α
,
φ
α
)
{\displaystyle (U_{\alpha },\ \varphi _{\alpha })}
(
U
α
,
x
α
,
y
α
)
{\displaystyle (U_{\alpha },\ x_{\alpha },\ y_{\alpha })}
[ 9]
x
α
=
(
x
α
1
,
…
,
x
α
p
)
,
{\displaystyle x_{\alpha }=\left(x_{\alpha }^{1},\dots ,x_{\alpha }^{p}\right),}
y
α
=
(
y
α
1
,
…
,
y
α
q
)
.
{\displaystyle y_{\alpha }=\left(y_{\alpha }^{1},\dots ,y_{\alpha }^{q}\right).}
在
φ
β
(
U
α
∩
U
β
)
{\displaystyle \varphi _{\beta }(U_{\alpha }\cap U_{\beta })}
[ 9]
g
α
β
(
x
β
,
y
β
)
=
φ
α
∘
φ
β
−
1
(
x
β
,
y
β
)
=
(
x
α
(
x
β
,
y
β
)
,
y
α
(
x
β
,
y
β
)
)
.
{\displaystyle g_{\alpha \beta }\left(x_{\beta },y_{\beta }\right)=\varphi _{\alpha }\circ \varphi _{\beta }^{-1}\left(x_{\beta },y_{\beta }\right)=\left(x_{\alpha }\left(x_{\beta },y_{\beta }\right),y_{\alpha }\left(x_{\beta },y_{\beta }\right)\right).}
U
α
{\displaystyle U_{\alpha }}
U
β
{\displaystyle U_{\beta }}
(
U
α
,
x
α
,
y
α
)
,
(
U
β
,
x
β
,
y
β
)
{\displaystyle (U_{\alpha },\ x_{\alpha },\ y_{\alpha }),\ (U_{\beta },\ x_{\beta },\ y_{\beta })}
P
⊂
U
α
{\displaystyle P\subset U_{\alpha }}
P
∩
U
β
{\displaystyle P\cap U_{\beta }}
U
β
{\displaystyle U_{\beta }}
U
α
,
U
β
{\displaystyle U_{\alpha },\ U_{\beta }}
y
α
,
y
β
{\displaystyle y_{\alpha },\ y_{\beta }}
∀
z
∈
U
α
∩
U
β
{\displaystyle \forall z\in U_{\alpha }\cap U_{\beta }}
y
α
=
y
α
(
x
β
,
y
β
)
=
y
α
(
y
β
)
{\displaystyle y_{\alpha }=y_{\alpha }(x_{\beta },y_{\beta })=y_{\alpha }(y_{\beta })}
與
x
β
{\displaystyle x_{\beta }}
[ 9]
葉狀圖冊的主要用處是將重疊的斑連接起來,形成葉狀結構;上述一般定義顯得有點笨拙,一個問題是,
(
U
α
,
φ
α
)
{\displaystyle (U_{\alpha },\ \varphi _{\alpha })}
(
U
β
,
φ
β
)
{\displaystyle (U_{\beta },\ \varphi _{\beta })}
若
U
∪
V
{\displaystyle {\mathcal {U}}\cup {\mathcal {V}}}
C
r
{\displaystyle C^{r}}
M 上兩具有相同餘維和光滑度的
C
r
{\displaystyle C^{r}}
U
,
V
{\displaystyle {\mathcal {U}},\ {\mathcal {V}}}
(
U
≈
V
)
{\displaystyle \left({\mathcal {U}}\thickapprox {\mathcal {V}}\right)}
[ 9]
證明 [ 9]
自反關係 和對稱關係 是直接的。要證傳遞關係 ,令
U
≈
V
{\displaystyle {\mathcal {U}}\thickapprox {\mathcal {V}}}
V
≈
W
{\displaystyle {\mathcal {V}}\thickapprox {\mathcal {W}}}
(
U
α
,
x
α
,
y
α
)
∈
U
,
(
W
λ
,
x
λ
,
y
λ
)
∈
W
{\displaystyle (U_{\alpha },\ x_{\alpha },\ y_{\alpha })\in {\mathcal {U}},\ (W_{\lambda },\ x_{\lambda },\ y_{\lambda })\in {\mathcal {W}}}
w
∈
U
α
∩
W
λ
{\displaystyle w\in U_{\alpha }\cap W_{\lambda }}
(
V
δ
,
x
δ
,
y
δ
)
∈
V
{\displaystyle (V_{\delta },\ x_{\delta },\ y_{\delta })\in {\mathcal {V}}}
w
∈
V
δ
{\displaystyle w\in V_{\delta }}
w 有屬於
U
α
∩
V
δ
∩
W
λ
{\displaystyle U_{\alpha }\cap V_{\delta }\cap W_{\lambda }}
y
δ
=
y
δ
(
y
λ
)
on
φ
λ
(
N
)
,
{\displaystyle y_{\delta }=y_{\delta }(y_{\lambda })\quad {\text{on}}\quad \varphi _{\lambda }(N),}
y
α
=
y
α
(
y
δ
)
on
φ
δ
(
N
)
,
{\displaystyle y_{\alpha }=y_{\alpha }(y_{\delta })\quad {\text{on}}\quad \varphi _{\delta }(N),}
由此
y
α
=
y
α
(
y
δ
(
y
λ
)
)
on
φ
δ
(
N
)
.
{\displaystyle y_{\alpha }=y_{\alpha }\left(y_{\delta }(y_{\lambda })\right)\quad {\text{on}}\quad \varphi _{\delta }(N).}
由於
w
∈
U
α
∩
W
λ
{\displaystyle w\in U_{\alpha }\cap W_{\lambda }}
y
α
(
x
λ
,
y
λ
)
{\displaystyle y_{\alpha }(x_{\lambda },\ y_{\lambda })}
x
λ
{\displaystyle x_{\lambda }}
U
≈
W
{\displaystyle {\mathcal {U}}\thickapprox {\mathcal {W}}}
[ 10]
規則葉狀圖冊中的圖。 上面定義的開集上的斑與橫截也是開的。不過,我們也可以談論閉的斑與橫截:若
(
U
,
φ
)
,
(
W
,
ψ
)
{\displaystyle (U,\ \varphi ),\ (W,\ \psi )}
U
¯
{\displaystyle {\overline {U}}}
U 的閉包 )是W 的子集,
φ
=
ψ
|
U
{\displaystyle \varphi =\psi |U}
φ
(
U
)
=
B
τ
×
B
⋔
,
{\displaystyle \varphi (U)=B_{\tau }\times B_{\pitchfork },}
ψ
|
U
¯
{\displaystyle \psi |{\overline {U}}}
φ
¯
{\displaystyle {\overline {\varphi }}}
U
¯
{\displaystyle {\overline {U}}}
B
¯
τ
×
B
¯
⋔
.
{\displaystyle {\overline {B}}_{\tau }\times {\overline {B}}_{\pitchfork }.}
符合以下條件的葉狀圖冊稱作規則的(regular):
∀
α
∈
A
,
U
¯
α
{\displaystyle \forall \alpha \in A,\ {\overline {U}}_{\alpha }}
(
W
α
,
ψ
α
)
{\displaystyle (W_{\alpha },\ \psi _{\alpha })}
φ
α
=
ψ
α
|
U
α
{\displaystyle \varphi _{\alpha }=\psi _{\alpha }|U_{\alpha }}
覆蓋
{
U
α
|
α
∈
A
}
{\displaystyle \{U_{\alpha }|\alpha \in A\}}
若
(
U
α
,
φ
α
)
,
(
U
β
,
φ
β
)
{\displaystyle (U_{\alpha },\ \varphi _{\alpha }),\ (U_{\beta },\ \varphi _{\beta })}
P
⊂
U
¯
α
{\displaystyle P\subset {\overline {U}}_{\alpha }}
U
¯
β
{\displaystyle {\overline {U}}_{\beta }}
[ 11] 根據性質 (1),坐標
x
α
,
y
α
{\displaystyle x_{\alpha },\ y_{\alpha }}
U
¯
α
{\displaystyle {\overline {U}}_{\alpha }}
x
¯
α
,
y
¯
α
{\displaystyle {\overline {x}}_{\alpha },\ {\overline {y}}_{\alpha }}
φ
¯
α
=
(
x
¯
α
,
y
¯
α
)
.
{\displaystyle {\overline {\varphi }}_{\alpha }=\left({\overline {x}}_{\alpha },{\overline {y}}_{\alpha }\right).}
U
α
∩
U
β
≠
∅
{\displaystyle U_{\alpha }\cap U_{\beta }\neq \varnothing }
y
¯
α
=
y
¯
α
(
x
¯
β
,
y
¯
β
)
{\displaystyle {\overline {y}}_{\alpha }={\overline {y}}_{\alpha }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right)}
x
¯
β
.
{\displaystyle {\overline {x}}_{\beta }.}
g
¯
α
β
=
φ
¯
α
∘
φ
¯
β
−
1
:
φ
¯
β
(
U
¯
α
∩
U
¯
β
)
→
φ
¯
α
(
U
¯
α
∩
U
¯
β
)
{\displaystyle {\overline {g}}_{\alpha \beta }={\overline {\varphi }}_{\alpha }\circ {\overline {\varphi }}_{\beta }^{-1}:{\overline {\varphi }}_{\beta }\left({\overline {U}}_{\alpha }\cap {\overline {U}}_{\beta }\right)\rightarrow {\overline {\varphi }}_{\alpha }\left({\overline {U}}_{\alpha }\cap {\overline {U}}_{\beta }\right)}
有公式[ 11]
g
¯
α
β
(
x
¯
β
,
y
¯
β
)
=
(
x
¯
α
(
x
¯
β
,
y
¯
β
)
,
y
¯
α
(
y
¯
β
)
)
.
{\displaystyle {\overline {g}}_{\alpha \beta }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right)=\left({\overline {x}}_{\alpha }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right),{\overline {y}}_{\alpha }\left({\overline {y}}_{\beta }\right)\right).}
類似論斷也適於開圖(無覆蓋線)。橫坐標映射
y
α
{\displaystyle y_{\alpha }}
浸沒
y
α
:
U
α
→
R
q
{\displaystyle y_{\alpha }:U_{\alpha }\rightarrow \mathbb {R} ^{q}}
公式
y
α
=
y
α
(
y
β
)
{\displaystyle y_{\alpha }=y_{\alpha }(y_{\beta })}
微分同胚
γ
α
β
:
y
β
(
U
α
∩
U
β
)
→
y
α
(
U
α
∩
U
β
)
.
{\displaystyle \gamma _{\alpha \beta }:y_{\beta }\left(U_{\alpha }\cap U_{\beta }\right)\rightarrow y_{\alpha }\left(U_{\alpha }\cap U_{\beta }\right).}
它們滿足上循環條件 ,即,在
y
δ
(
U
α
∩
U
β
∩
U
δ
)
{\displaystyle y_{\delta }(U_{\alpha }\cap U_{\beta }\cap U_{\delta })}
γ
α
δ
=
γ
α
β
∘
γ
β
δ
{\displaystyle \gamma _{\alpha \delta }=\gamma _{\alpha \beta }\circ \gamma _{\beta \delta }}
尤其是,[ 12]
γ
α
α
≡
y
α
(
U
α
)
,
{\displaystyle \gamma _{\alpha \alpha }\equiv y_{\alpha }\left(U_{\alpha }\right),}
γ
α
β
=
γ
β
α
−
1
.
{\displaystyle \gamma _{\alpha \beta }=\gamma _{\beta \alpha }^{-1}.}
用上述關於相干性和規則性的定義,可證明每個葉狀圖冊都有規則的相干細化 。[ 13]
證明 [ 13]
固定M 上的一個度量核一個葉狀圖冊
W
.
{\displaystyle {\mathcal {W}}.}
子覆蓋 ,如有必要,可假設
W
=
{
W
j
,
ψ
j
}
j
=
1
l
{\displaystyle {\mathcal {W}}=\left\{W_{j},\psi _{j}\right\}_{j=1}^{l}}
W
{\displaystyle {\mathcal {W}}}
勒貝格數 ,即直徑< ε的
∀
⊂
X
⊆
M
{\displaystyle \forall \subset X\subseteq M}
W
j
{\displaystyle W_{j}}
∀
x
∈
M
{\displaystyle \forall x\in M}
j 使得
x
∈
W
j
{\displaystyle x\in W_{j}}
(
U
x
,
φ
x
)
{\displaystyle (U_{x},\ \varphi _{x})}
x
∈
U
x
⊆
U
¯
x
⊂
W
j
,
{\displaystyle x\in U_{x}\subseteq {\overline {U}}_{x}\subset W_{j},}
φ
x
=
ψ
j
|
U
x
,
{\displaystyle \varphi _{x}=\psi _{j}|U_{x},}
d
i
a
m
(
U
x
)
<
ε
/
2.
{\displaystyle {\rm {diam}}(U_{x})<\varepsilon /2.}
設
U
x
⊂
W
k
(
k
≠
j
)
{\displaystyle U_{x}\subset W_{k}\ (k\neq j)}
ψ
k
=
(
x
k
,
y
k
)
(
y
k
:
W
k
→
R
q
)
{\displaystyle \psi _{k}=(x_{k},\ y_{k})\ (y_{k}:\ W_{k}\to \mathbb {R} ^{q})}
浸沒 ,以
W
k
{\displaystyle W_{k}}
y
k
{\displaystyle y_{k}}
y
k
:
U
x
→
R
q
.
{\displaystyle y_{k}:\ U_{x}\to \mathbb {R} ^{q}.}
這在
x
j
{\displaystyle x_{j}}
U
x
{\displaystyle U_{x}}
y
k
|
U
¯
x
{\displaystyle y_{k}|{\overline {U}}_{x}}
U
¯
x
{\displaystyle {\overline {U}}_{x}}
W
k
{\displaystyle W_{k}}
U
¯
x
{\displaystyle {\overline {U}}_{x}}
k < l < ∞ ,可以擇
U
x
{\displaystyle U_{x}}
U
x
⊂
W
k
{\displaystyle U_{x}\subset W_{k}}
U
¯
x
{\displaystyle {\overline {U}}_{x}}
W
k
{\displaystyle W_{k}}
{
(
U
x
,
φ
x
)
|
x
∈
M
}
{\displaystyle \{(U_{x},\ \varphi _{x})|x\in M\}}
U
=
{
U
i
,
φ
i
}
i
=
1
N
{\displaystyle {\mathcal {U}}=\left\{U_{i},\varphi _{i}\right\}_{i=1}^{N}}
U
i
∩
U
j
≠
0
,
d
i
a
m
(
U
i
∪
U
j
)
<
ε
{\displaystyle U_{i}\cap U_{j}\neq 0,\ {\rm {diam}}(U_{i}\cup U_{j})<\varepsilon }
k 使得
U
¯
i
∪
U
¯
j
⊆
W
k
{\displaystyle {\overline {U}}_{i}\cup {\overline {U}}_{j}\subseteq W_{k}}
U
¯
i
{\displaystyle {\overline {U}}_{i}}
U
¯
j
{\displaystyle {\overline {U}}_{j}}
W
k
{\displaystyle W_{k}}
U
¯
i
{\displaystyle {\overline {U}}_{i}}
U
¯
j
{\displaystyle {\overline {U}}_{j}}
U
{\displaystyle {\mathcal {U}}}
W
{\displaystyle {\mathcal {W}}}
若M 非緊,局部緊 性和第二可數性 允許我們選擇緊子集序列
{
K
i
}
i
=
0
∞
{\displaystyle \left\{K_{i}\right\}_{i=0}^{\infty }}
∀
i
≥
0
,
M
=
⋃
i
=
1
∞
K
i
,
K
i
⊂
i
n
t
K
i
+
1
{\displaystyle \forall i\geq 0,\ M=\bigcup _{i=1}^{\infty }K_{i},\ K_{i}\subset {\rm {int}}K_{i+1}}
W
=
{
W
j
,
ψ
j
}
j
=
0
∞
{\displaystyle {\mathcal {W}}=\left\{W_{j},\psi _{j}\right\}_{j=0}^{\infty }}
{
n
l
}
l
=
0
∞
{\displaystyle \left\{n_{l}\right\}_{l=0}^{\infty }}
W
l
=
{
W
j
,
ψ
j
}
j
=
0
n
l
{\displaystyle {\mathcal {W}}_{l}=\left\{W_{j},\psi _{j}\right\}_{j=0}^{n_{l}}}
K
l
{\displaystyle K_{l}}
δ
l
{\displaystyle \delta _{l}}
K
l
{\displaystyle K_{l}}
∂
K
l
+
1
{\displaystyle \partial K_{l+1}}
ε
l
>
0
{\displaystyle \varepsilon _{l}>0}
l
≥
1
,
ε
0
<
δ
0
/
2
{\displaystyle l\geq 1,\ \varepsilon _{0}<\delta _{0}/2}
ε
l
<
m
i
n
{
δ
l
/
2
,
ε
l
−
1
}
{\displaystyle \varepsilon _{l}<{\rm {min}}\{\delta _{l}/2,\ \varepsilon _{l-1}\}}
ε
l
{\displaystyle \varepsilon _{l}}
W
l
{\displaystyle {\mathcal {W}}_{l}}
K
l
{\displaystyle K_{l}}
W
l
+
1
{\displaystyle {\mathcal {W}}_{l+1}}
K
l
+
1
{\displaystyle K_{l+1}}
X
⊂
M
{\displaystyle X\subset M}
L
l
{\displaystyle L_{l}}
K
l
+
1
{\displaystyle K_{l+1}}
d
i
a
m
X
<
ε
l
{\displaystyle {\rm {diam}}X<\varepsilon _{l}}
X 位於
W
l
{\displaystyle {\mathcal {W}}_{l}}
W
l
+
1
{\displaystyle {\mathcal {W}}_{l+1}}
∀
x
∈
K
l
╲
i
n
t
K
l
−
1
{\displaystyle \forall x\in K_{l}\diagdown {\rm {int}}K_{l-1}}
(
U
x
,
φ
x
)
{\displaystyle (U_{x},\ \varphi _{x})}
U
¯
x
{\displaystyle {\overline {U}}_{x}}
W
j
{\displaystyle W_{j}}
∀
j
≤
n
l
,
φ
x
=
ψ
j
|
U
x
{\displaystyle \forall j\leq n_{l},\ \varphi _{x}=\psi _{j}|U_{x}}
d
i
a
m
U
¯
x
<
ε
l
/
2
{\displaystyle {\rm {diam}}{\overline {U}}_{x}<\varepsilon _{l}/2}
K
l
╲
i
n
t
K
l
−
1
{\displaystyle K_{l}\diagdown {\rm {int}}K_{l-1}}
{
U
i
,
φ
i
}
i
=
n
l
−
1
+
1
n
l
{\displaystyle \left\{U_{i},\varphi _{i}\right\}_{i=n_{l-1}+1}^{n_{l}}}
n
−
1
=
0
{\displaystyle n_{-1}=0}
U
=
{
U
i
,
φ
i
}
i
=
1
∞
{\displaystyle {\mathcal {U}}=\left\{U_{i},\varphi _{i}\right\}_{i=1}^{\infty }}
W
{\displaystyle {\mathcal {W}}}
W
{\displaystyle {\mathcal {W}}}
根據實現葉狀結構的方式,有幾種不同的定義。最常見方式是通過流形分解 ,得到
通過坐標函數
x
:
U
→
R
n
{\displaystyle x:\ U\to \mathbb {R} ^{n}}
定義 n 維流形M 的p -維
C
r
{\displaystyle C^{r}}
M 分解為不交 連通子流形
{
L
α
}
α
∈
A
{\displaystyle \{L_{\alpha }\}_{\alpha \in A}}
M 的點都有鄰域U 和局部
C
r
{\displaystyle C^{r}}
x
=
(
x
1
,
…
,
x
n
)
:
U
→
R
n
{\displaystyle x=(x^{1},\ \ldots ,\ x^{n}):\ U\to \mathbb {R} ^{n}}
L
α
{\displaystyle L_{\alpha }}
U
∩
L
α
{\displaystyle U\cap L_{\alpha }}
x
p
+
1
=
常数
,
…
,
x
n
=
常数
{\displaystyle x^{p+1}={\text{常数}},\ \ldots ,\ x^{n}={\text{常数}}}
F
=
{
L
α
}
α
∈
A
.
{\displaystyle {\mathcal {F}}=\{L_{\alpha }\}_{\alpha \in A}.}
[ 5]
葉的概念可以讓我們直觀地思考葉狀結構。若用稍微幾何化的定義,n 維流形M 的p 維葉狀結構
F
{\displaystyle {\mathcal {F}}}
M 的逐對不交、連通浸沒的p 維子流形(葉狀結構的葉)的集合
{
M
a
}
{\displaystyle \{M_{a}\}}
∀
x
∈
M
{\displaystyle \forall x\in M}
(
U
,
φ
)
{\displaystyle (U,\varphi )}
U 同胚於
R
n
{\displaystyle \mathbb {R} ^{n}}
x 使得對每片葉
M
a
{\displaystyle M_{a}}
U 相遇或為空集或為子空間的可數集 ,其在
φ
(
M
a
∩
U
)
{\displaystyle \varphi (M_{a}\cap U)}
φ
{\displaystyle \varphi }
p 維仿射子空間 。
葉狀結構局部上都是浸沒 ,允許下列定義
定義 令M 、Q 是n 維流形,q ≤n ,並令
f
:
M
→
Q
{\displaystyle f:\ M\to Q}
雅可比矩陣 )的秩為q ,則據隱函數定理 ,ƒ 在M 上誘導了余維為q 的葉狀結構,其中的葉定義為
x
∈
Q
,
f
−
1
(
x
)
.
{\displaystyle x\in Q,\ f^{-1}(x).}
[ 5]
這定義描述了n 維流形M 的p 維葉狀結構
F
{\displaystyle {\mathcal {F}}}
圖 (chart)
U
i
{\displaystyle U_{i}}
φ
i
:
U
i
→
R
n
{\displaystyle \varphi _{i}:U_{i}\to \mathbb {R} ^{n}}
這樣,對重疊對
U
i
,
U
j
{\displaystyle U_{i},\ U_{j}}
轉移函數
φ
i
j
:
R
n
→
R
n
{\displaystyle \varphi _{ij}:\ \mathbb {R} ^{n}\to \mathbb {R} ^{n}}
φ
i
j
=
φ
j
φ
i
−
1
{\displaystyle \varphi _{ij}=\varphi _{j}\varphi _{i}^{-1}}
形式為
φ
i
j
(
x
,
y
)
=
(
φ
i
j
1
(
x
)
,
φ
i
j
2
(
x
,
y
)
)
{\displaystyle \varphi _{ij}(x,y)=(\varphi _{ij}^{1}(x),\varphi _{ij}^{2}(x,y))}
其中x 表示前
q
=
n
−
p
{\displaystyle q=n-p}
y 表示後p 個坐標(co-ordinates),即
φ
i
j
1
:
R
q
→
R
q
φ
i
j
2
:
R
n
→
R
p
{\displaystyle {\begin{aligned}\varphi _{ij}^{1}:{}&\mathbb {R} ^{q}\to \mathbb {R} ^{q}\\\varphi _{ij}^{2}:{}&\mathbb {R} ^{n}\to \mathbb {R} ^{p}\end{aligned}}}
將轉移函數
φ
i
j
{\displaystyle \varphi _{ij}}
φ
i
j
1
(
x
)
,
φ
i
j
2
(
x
,
y
)
{\displaystyle \varphi _{ij}^{1}(x),\ \varphi _{ij}^{2}(x,y)}
g
¯
α
β
{\displaystyle {\overline {g}}_{\alpha \beta }}
y
¯
α
(
y
¯
β
)
,
x
¯
α
(
x
¯
β
,
y
¯
β
)
{\displaystyle {\overline {y}}_{\alpha }\left({\overline {y}}_{\beta }\right),\ {\overline {x}}_{\alpha }\left({\overline {x}}_{\beta },{\overline {y}}_{\beta }\right)}
q 的規則葉狀圖冊都與唯一的余維度為q 的葉狀結構
F
{\displaystyle {\mathcal {F}}}
[ 13]
證明[ 13]
令
U
=
{
U
a
,
φ
α
}
α
∈
A
{\displaystyle {\mathcal {U}}=\left\{U_{a},\varphi _{\alpha }\right\}_{\alpha \in A}}
q 的規則葉狀圖冊。在M 上定義等價關係:x ~ y ,若且唯若
∃
U
{\displaystyle \exists {\mathcal {U}}}
P
0
{\displaystyle P_{0}}
x
,
y
∈
P
0
{\displaystyle x,\ y\in P_{0}}
U
{\displaystyle {\mathcal {U}}}
L
=
{
P
0
,
P
1
,
…
,
P
p
}
{\displaystyle L=\{P_{0},\ P_{1},\ \dots ,\ P_{p}\}}
x
∈
P
0
,
y
∈
P
p
,
P
i
∩
P
i
−
1
≠
∅
(
1
≤
i
≤
p
)
{\displaystyle x\in P_{0},\ y\in P_{p},\ P_{i}\cap P_{i-1}\neq \varnothing \ (1\leq i\leq p)}
L 為連接x 、y 的長p 的斑鏈。
x
,
y
∈
P
0
{\displaystyle x,\ y\in P_{0}}
{
P
0
}
{\displaystyle \{P_{0}\}}
x 、y 的長度為0的斑鏈。~是等價關係,這很清楚;同樣明顯的是,等價類L 都是斑的並。由於
U
{\displaystyle {\mathcal {U}}}
L 在局部是維度為n-q的拓撲浸入(immerse)子流形。斑
P
⊂
L
{\displaystyle P\subset L}
L 上構成了n-q維的局部歐氏拓撲的基,L 在這拓撲中顯然是連通的。要檢驗L 是否為豪斯多夫空間 也是平凡的,主要問題是要證明L 第二可數 。由於斑都是第二可數的,所以對L 只需證L 中
U
{\displaystyle {\mathcal {U}}}
P
0
{\displaystyle P_{0}}
{
P
0
,
P
i
}
{\displaystyle \{P_{0},\ P_{i}\}}
P
0
{\displaystyle P_{0}}
p 長斑鏈,同樣可證明長度≤ p的斑鏈只有有限多條。根據~的定義,L 中所有
U
{\displaystyle {\mathcal {U}}}
P
0
{\displaystyle P_{0}}
正如證明所示,葉狀結構的葉是長度 ≤ p 的斑鏈的等價類,也是拓撲浸入豪斯多夫p 維子流形 。接着,我們將證明葉上斑的等價關係可用相干葉狀圖冊的等價來表示,即它們與葉狀結構的聯繫。更具體地說,若
U
,
V
{\displaystyle {\mathcal {U}},\ {\mathcal {V}}}
M 上的葉狀圖冊、且若
U
{\displaystyle {\mathcal {U}}}
F
{\displaystyle {\mathcal {F}}}
V
{\displaystyle {\mathcal {V}}}
F
{\displaystyle {\mathcal {F}}}
U
,
V
{\displaystyle {\mathcal {U}},\ {\mathcal {V}}}
[ 10]
現在很明顯,M 上的葉狀結構與葉狀圖冊間的關聯關係產生了M 的葉狀結構集同葉狀圖冊的相干類集之間的一一對應,換句話說,M 上余維為q 的
C
r
{\displaystyle C^{r}}
F
{\displaystyle {\mathcal {F}}}
q 的
C
r
{\displaystyle C^{r}}
[ 14] 佐恩引理 ,葉狀圖冊相干類顯然包含唯一的最大葉狀圖冊。於是,
定義 M 上余維為q 的
C
r
{\displaystyle C^{r}}
M 上余維為q 的最大葉狀
C
r
{\displaystyle C^{r}}
[ 14]
實踐中,通常用較小的葉狀圖冊表示葉狀結構,通常還要求是規則的。
在圖
U
i
{\displaystyle U_{i}}
x
=
常数
{\displaystyle x={\text{常数}}}
U
j
{\displaystyle U_{j}}
連通 單射浸入子流形 ,就是葉狀結構的葉 (leaf)。
若縮小圖
U
i
{\displaystyle U_{i}}
U
i
x
×
U
i
y
{\displaystyle U_{ix}\times U_{iy}}
U
i
x
⊂
R
n
−
p
,
U
i
y
⊂
R
p
.
U
i
y
{\displaystyle U_{ix}\subset \mathbb {R} ^{n-p},\ U_{iy}\subset \mathbb {R} ^{p}.\ \ U_{}iy}
U
i
x
{\displaystyle U_{ix}}
U
i
{\displaystyle U_{i}}
y
0
∈
U
i
y
{\displaystyle y_{0}\in U_{iy}}
U
i
x
×
{
y
0
}
{\displaystyle U_{ix}\times \{y_{0}\}}
U
i
{\displaystyle U_{i}}
橫截 面 。注意,由於單值性 的原因,全局橫截面可能不存在。
r = 0的情形比較特殊。實踐中出現的
C
0
{\displaystyle C^{0}}
C
r
,
0
{\displaystyle C^{r,\ 0}}
定義 若葉狀圖冊的相應相干類包含規則葉狀圖冊
{
U
α
,
x
α
,
y
α
}
α
∈
A
{\displaystyle \{U_{\alpha },\ x_{\alpha },\ y_{\alpha }\}_{\alpha \in A}}
g
α
β
(
x
β
,
y
β
)
=
(
x
α
(
x
β
,
y
β
)
,
y
α
(
y
β
)
)
.
{\displaystyle g_{\alpha \beta }(x_{\beta },y_{\beta })=(x_{\alpha }(x_{\beta },y_{\beta }),y_{\alpha }(y_{\beta })).}
屬於
C
k
{\displaystyle C^{k}}
x
α
{\displaystyle x_{\alpha }}
x
β
{\displaystyle x_{\beta }}
C
r
{\displaystyle C^{r}}
r 、與
x
β
{\displaystyle x_{\beta }}
(
x
β
,
y
β
{\displaystyle (x_{\beta },\ y_{\beta }}
C
k
{\displaystyle C^{k}}
F
{\displaystyle {\mathcal {F}}}
C
r
,
k
(
r
>
k
≥
0
)
{\displaystyle C^{r,\ k}\ (r>k\geq 0)}
[ 14]
上述定義是所謂「葉狀空間」的更一般概念。我們可以放寬橫截的條件為
R
q
{\displaystyle \mathbb {R} ^{q}}
y
α
{\displaystyle y_{\alpha }}
Z 中取值。斑仍是
R
q
{\displaystyle \mathbb {R} ^{q}}
y
α
(
y
β
)
{\displaystyle y_{\alpha }(y_{\beta })}
x
α
(
x
β
,
y
β
)
{\displaystyle x_{\alpha }(x_{\beta },\ y_{\beta })}
x
β
{\displaystyle x_{\beta }}
C
r
{\displaystyle C^{r}}
r 、與
x
β
{\displaystyle x_{\beta }}
(
x
β
,
y
β
)
{\displaystyle (x_{\beta },\ y_{\beta })}
M 、Z 為局部緊可測第二可數空間 。這似乎是很狂野的推廣,但在一些情形下很有用。[ 15]
令
(
M
,
F
)
{\displaystyle (M,\ {\mathcal {F}})}
L 是
F
{\displaystyle {\mathcal {F}}}
s 是L 中的路徑,我們感興趣的是M 中s 的鄰域中葉狀結構的行為。直觀地說,在葉上可以沿路徑s 行走,同時關注附近所有葉。在他(以下寫作s (t ))行走時,一些葉可能會「掉落」、變得不可見;另一些可能會突然進入可視範圍,漸漸接近L ;還有些可能會以接近平行的方式跟隨L ,或垂直地打轉之類。若s 是環路,則隨着t 增大,s (t )會反覆回到同一個點s (t 0 ),每次都會有更多葉螺旋狀地進入或離開視野。這種行為經過適當的形式化,叫做葉狀結構的完整性(holonomy)。
完整性在葉狀流形上有多種具體實現方式:葉狀叢(foliated bundle)的總完整群、一般葉狀流形的完整偽群、一般葉狀流形的虧格完整廣群、葉的虧格完整群、葉的無窮小完整群。
最容易理解的完整性是葉狀叢的總完整性,這是龐加萊映射 概念的推廣。
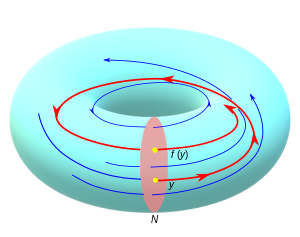
橫截面(cross section)N 與第一回歸映射(first return map)f ,其中
M
=
S
1
×
D
2
,
N
=
D
2
.
{\displaystyle M=S^{1}\times D^{2},\ N=D^{2}.}
「第一回歸映射」 來自動力系統理論。令
Φ
t
{\displaystyle \Phi _{t}}
n -流形上的非奇異
C
r
(
r
≥
1
)
{\displaystyle C^{r}\ (r\geq 1)}
M 是個回旋加速器 或流體的閉合迴路。若M 有界,則假定流與界相切。流生成了1維葉狀結構
F
{\displaystyle {\mathcal {F}}}
F
{\displaystyle {\mathcal {F}}}
N ,即N 是M 的n-1維緊正合嵌入的
C
r
{\displaystyle C^{r}}
F
{\displaystyle {\mathcal {F}}}
N ,每條流線都與N 相遇。由於N 的維度與葉的維度是互補的,橫截性條件是
T
y
(
M
)
=
T
y
(
F
)
⊕
T
y
(
N
)
for each
y
∈
N
.
{\displaystyle T_{y}(M)=T_{y}({\mathcal {F}})\oplus T_{y}(N){\text{ for each }}y\in N.}
令
y
∈
N
{\displaystyle y\in N}
M 中所有序列
{
Φ
t
k
(
y
)
}
k
=
1
∞
{\displaystyle \left\{\Phi _{t_{k}}(y)\right\}_{k=1}^{\infty }}
ω -極限集合 ω(y),其中
t
k
{\displaystyle t_{k}}
z
=
lim
k
→
∞
Φ
t
k
∈
ω
(
y
)
,
{\displaystyle z=\lim _{k\rightarrow \infty }\Phi _{t_{k}}\in \omega (y),}
t
∗
∈
R
{\displaystyle t^{*}\in \mathbb {R} }
Φ
t
∗
(
z
)
∈
N
{\displaystyle \Phi _{t^{*}}(z)\in N}
lim
k
→
∞
Φ
t
k
+
t
∗
(
y
)
=
Φ
t
∗
(
z
)
∈
N
.
{\displaystyle \lim _{k\to \infty }\Phi _{t_{k}+t^{\ast }}(y)=\Phi _{t^{\ast }}(z)\in N.}
由於N 是緊的,
F
{\displaystyle {\mathcal {F}}}
N ,因此集合
{
t
>
0
|
Φ
t
(
y
)
∈
N
}
{\displaystyle \{t>0|\Phi _{t}(y)\in N\}}
{
τ
k
(
y
)
}
k
=
1
∞
{\displaystyle \{\tau _{k}(y)\}_{k=1}^{\infty }}
當
y
∈
N
{\displaystyle y\in N}
τ
(
y
)
=
τ
1
(
y
)
{\displaystyle \tau (y)=\tau _{1}(y)}
τ
∈
C
r
(
N
)
{\displaystyle \tau \in C^{r}(N)}
∀
y
∈
N
,
Φ
t
(
y
)
∉
N
,
0
<
t
<
τ
(
y
)
,
Φ
τ
(
y
)
(
y
)
∈
N
.
{\displaystyle \forall y\in N,\ \Phi _{t}(y)\notin N,\ 0<t<\tau (y),\ \Phi _{\tau (y)}(y)\in N.}
定義
f
:
N
→
N
,
f
(
y
)
=
Φ
τ
(
y
)
(
y
)
.
{\displaystyle f:\ N\to N,\ f(y)=\Phi _{\tau (y)}(y).}
C
r
{\displaystyle C^{r}}
f
−
1
{\displaystyle f^{-1}}
f
∈
D
i
f
f
r
(
N
)
{\displaystyle f\in {\rm {Diff}}^{r}(N)}
第一回歸時間 。雖然第一回歸時間取決於流的參數化,但f 顯然只取決於有向葉狀結構
F
{\displaystyle {\mathcal {F}}}
Φ
t
{\displaystyle \Phi _{t}}
C
r
{\displaystyle C^{r}}
τ
≡
1.
{\displaystyle \tau \equiv 1.}
流有橫截面N的假設是很受限的,意味着M 是
S
1
{\displaystyle S^{1}}
R
×
N
{\displaystyle \mathbb {R} \times N}
∼
f
{\displaystyle \sim _{f}}
(
t
,
y
)
∼
f
(
t
−
1
,
f
(
y
)
)
.
{\displaystyle (t,y)\sim _{f}(t-1,f(y)).}
等價地,這是加法群Z 在
R
×
N
{\displaystyle \mathbb {R} \times N}
∀
k
∈
Z
,
∀
(
t
,
y
)
∈
R
×
N
,
k
⋅
(
t
,
y
)
=
(
t
−
k
,
f
k
(
y
)
)
.
{\displaystyle \forall k\in \mathbb {Z} ,\ \forall (t,\ y)\in \mathbb {R} \times N,\ k\cdot (t,y)=(t-k,f^{k}(y)).}
f 的映射圓柱定義為
C
r
{\displaystyle C^{r}}
M
f
=
(
R
×
N
)
/
∼
f
.
{\displaystyle M_{f}=(\mathbb {R} \times N)/{\sim _{f}}.}
由第一回歸映射f 的定義與第一回歸時間
τ
≡
1
{\displaystyle \tau \equiv 1}
Φ
:
R
×
N
→
M
.
{\displaystyle \Phi :\mathbb {R} \times N\rightarrow M.}
流的定義可誘導一個規範
C
r
{\displaystyle C^{r}}
φ
:
M
f
→
M
.
{\displaystyle \varphi :M_{f}\rightarrow M.}
若記
M
f
=
M
{\displaystyle M_{f}=M}
R
×
N
{\displaystyle \mathbb {R} \times N}
R 的投影誘導了
C
r
{\displaystyle C^{r}}
π
:
M
→
R
/
Z
=
S
1
{\displaystyle \pi :M\rightarrow \mathbb {R} /\mathbb {Z} =S^{1}}
使M 變為圓上纖維叢 的總空間。這只是
S
1
×
D
2
{\displaystyle S^{1}\times D^{2}}
S
1
{\displaystyle S^{1}}
F
{\displaystyle {\mathcal {F}}}
L 的叢投影π是覆蓋映射
π
:
L
→
S
1
{\displaystyle \pi :\ L\to S^{1}}
以
x
0
∈
S
1
{\displaystyle x_{0}\in S^{1}}
0
+
Z
{\displaystyle 0+\mathbb {Z} }
π
−
1
(
x
0
)
{\displaystyle \pi ^{-1}(x_{0})}
N 。對
S
1
{\displaystyle S^{1}}
x
0
{\displaystyle x_{0}}
s ,同倫類
[
s
]
∈
π
1
(
S
1
,
x
0
)
{\displaystyle [s]\in \pi _{1}(S^{1},\ x_{0})}
d
e
g
s
∈
Z
{\displaystyle {\rm {deg}}s\in \mathbb {Z} }
s 提升到每條流線中的一條路徑,很明顯提升
s
y
{\displaystyle s_{y}}
y
∈
N
{\displaystyle y\in N}
f
k
(
y
)
∈
N
(
k
=
d
e
g
s
)
{\displaystyle f^{k}(y)\in N\ (k={\rm {deg}}s)}
f
k
∈
D
i
f
f
r
(
N
)
{\displaystyle f^{k}\in {\rm {Diff}}^{r}(N)}
h
s
{\displaystyle h_{s}}
s 的總整體性。由於只取決於[s ],因此定義了同胚
h
:
π
1
(
S
1
,
x
0
)
→
Diff
r
(
N
)
,
{\displaystyle h:\pi _{1}(S^{1},x_{0})\rightarrow \operatorname {Diff} ^{\,r}(N),}
稱作葉狀叢的總整體同胚。
更直觀地運用纖維叢,令
(
M
,
F
)
{\displaystyle (M,\ {\mathcal {F}})}
q 的葉狀n -流形,令
π
:
M
→
B
{\displaystyle \pi :\ M\to B}
q 維纖維F 與連通基空間B 。假設所有這些結構都屬於
C
r
(
0
≤
r
≤
∞
)
{\displaystyle C^{r}\ (0\leq r\leq \infty )}
r = 0,B 支持一個
C
1
{\displaystyle C^{1}}
B 上的最大
C
1
{\displaystyle C^{1}}
C
∞
{\displaystyle C^{\infty }}
B 如所期望那般光滑並不失一般性。最後,
∀
x
∈
B
{\displaystyle \forall x\in B}
x 有連通開鄰域
U
⊆
B
{\displaystyle U\subseteq B}
π
−
1
(
U
)
→
φ
U
×
F
π
↓
↓
p
U
→
id
U
{\displaystyle {\begin{matrix}\pi ^{-1}(U)&{\xrightarrow {\varphi }}&U\times {F}\\\scriptstyle {\pi }{\Bigg \downarrow }&{\qquad }&{\Bigg \downarrow }{\scriptstyle {p}}\\U&{\xrightarrow {\text{id}}}&U\end{matrix}}}
其中φ 是
C
r
{\displaystyle C^{r}}
r = 0則是同胚),將
F
∣
π
−
1
(
U
)
{\textstyle {\mathcal {F}}\mid \pi ^{-1}(U)}
{
U
×
{
y
}
}
y
∈
F
{\displaystyle \{U\times \{y\}\}_{y\in F}}
F
∣
π
−
1
(
U
)
{\textstyle {\mathcal {F}}\mid \pi ^{-1}(U)}
L
∩
π
−
1
(
U
)
{\displaystyle L\cap \pi ^{-1}(U)}
L 是
F
{\displaystyle {\mathcal {F}}}
C
r
{\displaystyle C^{r}}
(
M
,
F
,
π
)
{\displaystyle (M,\ {\mathcal {F}},\ \pi )}
F
{\displaystyle {\mathcal {F}}}
F
{\displaystyle {\mathcal {F}}}
F
{\displaystyle {\mathcal {F}}}
L 的限制是覆蓋映射
π
:
L
→
B
{\displaystyle \pi :\ L\to B}
F
x
=
π
−
1
(
x
)
{\displaystyle F_{x}=\pi ^{-1}(x)}
F
{\displaystyle {\mathcal {F}}}
F
{\displaystyle {\mathcal {F}}}
葉狀結構
F
{\displaystyle {\mathcal {F}}}
B 的覆蓋空間。這個問題的一個簡單版本是
R
2
{\displaystyle \mathbb {R} ^{2}}
π
:
R
2
→
R
,
{\displaystyle \pi :\mathbb {R} ^{2}\rightarrow \mathbb {R} ,}
π
(
x
,
y
)
=
x
,
{\displaystyle \pi (x,y)=x,}
但有無限多葉缺失了y 軸。在相應的圖像中,「有箭頭的」葉以及它們上面所有的葉都漸進於x = 0軸。一般稱這種葉狀結構為相對於纖維是不完備的,即當參數
x
∈
B
{\displaystyle x\in B}
x
0
∈
B
{\displaystyle x_{0}\in B}
L ,和一條連續路徑
s
:
[
0
,
a
)
→
L
{\displaystyle s:\ [0,\ a)\to L}
lim
t
→
a
−
π
(
s
(
t
)
)
=
x
0
∈
B
{\displaystyle \lim _{t\to a-}\pi (s(t))=x_{0}\in B}
lim
t
→
a
−
s
(
t
)
{\displaystyle \lim _{t\to a-}s(t)}
L 的流形拓撲中不存在。這類似於不完備流,某些流線會在有限時間內發散。雖然這樣的葉L 可能在別處與
π
−
1
(
x
0
)
{\displaystyle \pi ^{-1}(x_{0})}
x
0
{\displaystyle x_{0}}
B 在π下的的覆蓋空間。F 是緊的時,
F
{\displaystyle {\mathcal {F}}}
(
M
,
F
,
π
)
{\textstyle (M,{\mathcal {F}},\pi )}
B 上有圖冊
U
=
{
U
α
,
x
α
}
α
∈
A
{\displaystyle {\mathcal {U}}=\{U_{\alpha },\ x_{\alpha }\}_{\alpha \in A}}
φ
α
:
π
−
1
(
U
α
)
→
U
α
×
F
{\displaystyle \varphi _{\alpha }:\ \pi ^{-1}(U_{\alpha })\to U_{\alpha }\times F}
F
|
π
−
1
(
U
α
)
{\displaystyle {\mathcal {F}}|\pi ^{-1}(U_{\alpha })}
W
α
=
π
−
1
(
U
α
)
{\displaystyle W_{\alpha }=\pi ^{-1}(U_{\alpha })}
φ
α
=
(
x
α
,
y
α
)
{\displaystyle \varphi _{\alpha }=(x_{\alpha },\ y_{\alpha })}
x
α
{\displaystyle x_{\alpha }}
x
α
∘
π
,
y
α
:
π
−
1
(
U
α
)
→
F
{\displaystyle x_{\alpha }\circ \pi ,\ y_{\alpha }:\ \pi ^{-1}(U_{\alpha })\to F}
φ
α
{\displaystyle \varphi _{\alpha }}
U
α
×
F
→
F
{\displaystyle U_{\alpha }\times F\to F}
圖冊
W
=
{
W
α
,
x
α
,
y
α
}
α
∈
A
{\displaystyle {\mathcal {W}}=\{W_{\alpha },\ x_{\alpha },\ y_{\alpha }\}_{\alpha \in A}}
W
α
{\displaystyle W_{\alpha }}
y
α
{\displaystyle y_{\alpha }}
y
α
{\displaystyle y_{\alpha }}
F 相同。由於預設了B 支持某個
C
∞
{\displaystyle C^{\infty }}
懷特黑德定理 ,可在B 上固定一個黎曼度量,擇圖冊
U
{\displaystyle {\mathcal {U}}}
U
α
∩
U
β
{\displaystyle U_{\alpha }\cap U_{\beta }}
W
α
{\displaystyle W_{\alpha }}
W
β
{\displaystyle W_{\beta }}
γ
=
{
γ
α
β
}
α
,
β
∈
A
{\displaystyle \gamma =\left\{\gamma _{\alpha \beta }\right\}_{\alpha ,\beta \in A}}
γ
α
β
=
y
α
∘
y
β
−
1
:
F
→
F
.
{\displaystyle \gamma _{\alpha \beta }=y_{\alpha }\circ y_{\beta }^{-1}:F\rightarrow F.}
考慮n 維空間,是由前n-p個坐標為常數的點組成的子空間之積。這可以用一張圖(chart)表示,其基本原理是
R
n
=
R
n
−
p
×
R
p
{\displaystyle \mathbb {R} ^{n}=\mathbb {R} ^{n-p}\times \mathbb {R} ^{p}}
R
p
{\displaystyle \mathbb {R} ^{p}}
R
n
−
p
{\displaystyle \mathbb {R} ^{n-p}}
n = 3、p = 2,可以類比三維空間:書的2維葉由(1維)頁碼枚舉。
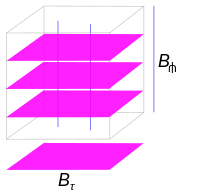
較平凡的葉狀結構例子是積
M
=
B
×
F
{\displaystyle M=B\times F}
F
b
=
{
b
}
×
F
,
b
∈
B
{\displaystyle F_{b}=\{b\}\times F,\ b\in B}
M 的另一個葉狀結構由
B
f
=
B
×
{
f
}
,
f
∈
F
{\displaystyle B_{f}=B\times \{f\},\ f\in F}
對流形F 而言,
G
=
H
o
m
e
o
(
F
)
{\displaystyle G={\rm {Homeo}}(F)}
G -叢是更一般的一類。給定表示
ρ
:
π
1
(
B
)
→
H
o
m
e
o
(
F
)
{\displaystyle \rho :\ \pi _{1}(B)\to {\rm {Homeo}}(F)}
H
o
m
e
o
(
F
)
{\displaystyle {\rm {Homeo}}(F)}
M
=
(
B
~
×
F
)
/
π
1
B
{\displaystyle M=\left({\widetilde {B}}\times F\right)/\pi _{1}B}
π
1
(
B
)
{\displaystyle \pi _{1}(B)}
甲板變換 作用於萬有覆蓋
B
~
{\displaystyle {\widetilde {B}}}
F 。
平坦叢符合纖維叢 的框架。若有流形F 使得
∀
b
∈
B
{\displaystyle \forall b\in B}
U 使得有同胚
φ
:
π
−
1
(
U
)
→
U
×
F
(
π
=
p
1
φ
,
p
1
:
U
×
F
→
U
)
{\displaystyle \varphi :\pi ^{-1}(U)\to U\times F\ (\pi =p_{1}\varphi ,\ p_{1}:\ U\times F\to U)}
p 1 是到第一個因子的投影),則流形之間的映射
π
:
M
→
B
{\displaystyle \pi :\ M\to B}
F
b
:=
π
−
1
(
{
b
}
)
,
b
∈
B
{\displaystyle F_{b}:=\pi ^{-1}(\{b\}),b\in B}
L 與B 同構,前者是豪斯多夫流形。
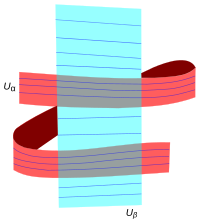
若
M
→
N
{\displaystyle M\to N}
F 是N 上的葉狀結構,則其拉回到M 上的葉狀結構。更一般地,若映射只是分歧覆蓋 (分歧軌跡 橫截於葉狀結構),則葉狀結構就可以被拉回。
若
M
n
→
N
q
,
(
q
≤
n
)
{\displaystyle M^{n}\to N^{q},\ (q\leq n)}
浸沒 ,則據反函數定理 ,浸沒的纖維的連通組分定義了M 的余維為q 的葉狀結構。纖維叢 是這種類型的一個例子。
不是纖維叢的浸沒的一個例子是
{
f
:
[
−
1
,
1
]
×
R
→
R
f
(
x
,
y
)
=
(
x
2
−
1
)
e
y
{\displaystyle {\begin{cases}f:[-1,1]\times \mathbb {R} \to \mathbb {R} \\f(x,y)=(x^{2}-1)e^{y}\end{cases}}}
這種浸沒產生了
[
−
1
,
1
]
×
R
{\displaystyle [-1,\ 1]\times \mathbb {R} }
Z
{\displaystyle \mathbb {Z} }
z
(
x
,
y
)
=
(
x
,
y
+
n
)
,
or
z
(
x
,
y
)
=
(
(
−
1
)
n
x
,
y
)
{\displaystyle z(x,y)=(x,y+n),\quad {\text{or}}\quad z(x,y)=\left((-1)^{n}x,y\right)}
其中
(
x
,
y
)
∈
[
−
1
,
1
]
×
R
,
n
∈
Z
{\displaystyle (x,\ y)\in [-1,\ 1]\times \mathbb {R} ,\ n\in \mathbb {Z} }
Z
∖
(
[
−
1
,
1
]
×
R
)
{\displaystyle \mathbb {Z} \backslash ([-1,\ 1]\times \mathbb {R} )}
定義一個潛沒
{
f
:
D
n
×
R
→
R
f
(
r
,
θ
,
t
)
:=
(
r
2
−
1
)
e
t
{\displaystyle {\begin{cases}f:D^{n}\times \mathbb {R} \to \mathbb {R} \\f(r,\theta ,t):=(r^{2}-1)e^{t}\end{cases}}}
其中
(
r
,
θ
)
∈
[
0
,
1
]
×
S
n
−
1
{\displaystyle (r,\ \theta )\in [0,\ 1]\times S^{n-1}}
n 維圓盤
D
n
{\displaystyle D^{n}}
D
n
×
R
{\displaystyle D^{n}\times \mathbb {R} }
Z 作用下是不變的:
z
(
x
,
y
)
=
(
x
,
y
+
z
)
(
(
x
,
y
)
∈
D
n
×
R
,
z
∈
Z
)
{\displaystyle z(x,y)=(x,y+z)\ ((x,\ y)\in D^{n}\times \mathbb {R} ,\ z\in \mathbb {Z} )}
Z
∖
(
D
n
×
R
)
{\displaystyle \mathbb {Z} \backslash (D^{n}\times \mathbb {R} )}
n 維里布葉狀結構 ,其葉空間不是豪斯多夫的。
對於n = 2,這給出了實心環面的葉狀結構,可由沿邊界粘合兩個實心環面,來定義3-球的里布葉狀結構。奇數維球
S
2
n
+
1
{\displaystyle S^{2n+1}}
[ 16]
若G 是李群 、H 是李子群,則G 就會被H 的陪集 葉化。若H 在G 中閉合 ,則商空間
G
/
H
{\displaystyle G/H}
豪斯多夫 )流形,將G 轉化為纖維叢,纖維H 、基為
G
/
H
{\displaystyle G/H}
主 的,具有結構群H 。
令G 是光滑作用於流形M 的李群。若作用是局部自由作用或自由作用,則G 的軌道定義了M 的一個葉狀結構。
若
X
~
{\displaystyle {\tilde {X}}}
X
~
{\displaystyle {\tilde {X}}}
x
∈
M
{\displaystyle x\in M}
X
~
{\displaystyle {\tilde {X}}}
x 的坐標鄰域
(
U
,
x
1
,
,
…
,
x
n
)
{\displaystyle (U,\ x^{1},\ ,\ldots ,\ x^{n})}
−
ε
<
x
i
<
ε
,
1
≤
i
≤
n
,
{\displaystyle -\varepsilon <x^{i}<\varepsilon ,\quad 1\leq i\leq n,}
∂
∂
x
1
=
X
~
∣
U
.
{\displaystyle {\frac {\partial }{\partial x^{1}}}={\tilde {X}}\mid U.}
從幾何角度來看,
X
~
∣
U
{\displaystyle {\tilde {X}}\mid U}
x
i
=
c
i
,
2
≤
i
≤
n
,
{\displaystyle x^{i}=c^{i},\quad 2\leq i\leq n,}
其中所有的
|
c
i
|
<
ε
.
{\displaystyle |c^{i}|<\varepsilon .}
M 本身的第二可數性排除。要求
X
~
{\displaystyle {\tilde {X}}}
M 是緊的),從而要求每片葉都是流線,就可以避開這個難題。
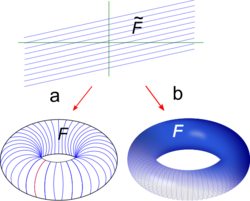
R
2
{\displaystyle \mathbb {R} ^{2}}
F
~
{\displaystyle {\mathcal {\tilde {F}}}}
T
2
{\displaystyle T^{2}}
F
{\displaystyle {\mathcal {F}}}
2-環面上的無理旋轉 環面
T
2
{\displaystyle T^{2}}
R
2
{\displaystyle \mathbb {R} ^{2}}
X
~
≡
[
a
b
]
{\displaystyle {\tilde {X}}\equiv {\begin{bmatrix}a\\b\end{bmatrix}}}
對
R
2
{\displaystyle \mathbb {R} ^{2}}
T
2
=
R
2
/
Z
2
{\displaystyle T^{2}=\mathbb {R} ^{2}/\mathbb {Z} ^{2}}
X 。假定a ≠ 0。
X
~
{\displaystyle {\tilde {X}}}
R
2
{\displaystyle \mathbb {R} ^{2}}
F
~
{\displaystyle {\mathcal {\tilde {F}}}}
θ
=
b
/
a
{\displaystyle \theta =b/a}
X 產生的
T
2
{\displaystyle T^{2}}
F
{\displaystyle {\mathcal {F}}}
F
~
{\displaystyle {\mathcal {\tilde {F}}}}
L
~
=
{
(
x
0
+
t
a
,
y
0
+
t
b
)
}
t
∈
R
.
{\displaystyle {\tilde {L}}=\{(x_{0}+ta,y_{0}+tb)\}_{t\in \mathbb {R} }.}
若斜率是有理 的,則所有葉都是與圓 同胚 的閉合曲線。這時,可取
a
,
b
∈
Z
{\displaystyle a,\ b\in \mathbb {Z} }
t
∈
R
{\displaystyle t\in \mathbb {R} }
L
~
{\displaystyle {\tilde {L}}}
t
∈
t
0
+
Z
{\displaystyle t\in t_{0}+\mathbb {Z} }
T
2
{\displaystyle T^{2}}
F
{\displaystyle {\mathcal {F}}}
L 是
T
2
{\displaystyle T^{2}}
L 是任意的,所以
F
{\displaystyle {\mathcal {F}}}
T
2
{\displaystyle T^{2}}
π
:
T
2
→
S
1
{\displaystyle \pi :\ T^{2}\to S^{1}}
若斜率是無理 的,則葉是非緊的,同胚於非緊實線 ,在環面中稠密 (參無理旋轉 )。每個點
(
x
0
,
y
0
)
{\displaystyle (x_{0},\ y_{0})}
利奧波德·克羅內克 與
克羅內克稠密性定理 若實數θ不等於π的所有有理倍數,則集合
{
e
i
n
θ
|
n
∈
Z
}
{\displaystyle \{e^{in\theta }|n\in \mathbb {Z} \}}
用平行線對
R
n
{\displaystyle \mathbb {R} ^{n}}
n -環面
R
n
/
Z
n
{\displaystyle \mathbb {R} ^{n}/\mathbb {Z} ^{n}}
平坦叢不僅有對纖維的線性結構,還有橫截於纖維的葉狀結構,其葉為
L
f
:=
{
p
(
b
~
,
f
)
:
b
~
∈
B
~
}
,
for
f
∈
F
,
{\displaystyle L_{f}:=\left\{p\left({\tilde {b}},f\right):{\tilde {b}}\in {\widetilde {B}}\right\},\quad {\mbox{ for }}f\in F,}
其中
p
:
B
~
×
F
→
M
{\displaystyle p:\ {\widetilde {B}}\times F\to M}
ρ
:
π
1
(
B
)
→
H
o
m
e
o
(
F
)
{\displaystyle \rho :\ \pi _{1}(B)\to {\rm {Homeo}}(F)}
具體地說,若
B
=
S
1
{\displaystyle B=S^{1}}
φ
:
F
→
F
{\displaystyle \varphi :F\to F}
F 的同胚,則
φ
{\displaystyle \varphi }
ρ
:
Z
→
H
o
m
e
o
(
F
)
{\displaystyle \rho :\ \mathbb {Z} \to {\rm {Homeo}}(F)}
ρ
(
z
)
=
Φ
z
{\displaystyle \rho (z)=\Phi ^{z}}
L
=
F
/
∼
{\displaystyle L={\mathcal {F}}/\sim }
n
∈
Z
,
y
=
Φ
n
(
x
)
,
x
∼
y
{\displaystyle n\in \mathbb {Z} ,\ y=\Phi ^{n}(x),\ x\sim y}
緯懸葉狀結構最簡單的例子是q 維流形X 。令
f
:
X
→
X
{\displaystyle f:\ X\to X}
M
=
S
1
×
f
X
{\displaystyle M=S^{1}\times _{f}X}
[
0
,
1
]
×
X
{\displaystyle [0,\ 1]\times X}
(
1
,
x
)
∼
(
0
,
f
(
x
)
)
{\displaystyle (1,\ x)\sim (0,\ f(x))}
M
=
S
1
×
f
X
=
[
0
,
1
]
×
X
{\displaystyle M=S^{1}\times _{f}X=[0,\ 1]\times X}
則,M 自動攜帶兩個葉狀結構:
F
2
{\displaystyle {\mathcal {F}}_{2}}
F
2
,
t
=
{
(
t
,
x
)
∼
:
x
∈
X
}
{\displaystyle F_{2,\ t}=\{(t,\ x)_{\sim }:\ x\in X\}}
F
1
{\displaystyle {\mathcal {F}}_{1}}
F
2
,
x
0
=
{
(
t
,
x
)
:
t
∈
[
0
,
1
]
,
x
∈
O
x
0
}
{\displaystyle F_{2,\ x_{0}}=\{(t,\ x):\ t\in [0,\ 1],\ x\in O_{x_{0}}\}}
O
x
0
{\displaystyle O_{x_{0}}}
O
x
0
=
{
…
,
f
−
2
(
x
0
)
,
f
−
1
(
x
0
)
,
x
0
,
f
(
x
0
)
,
f
2
(
x
0
)
,
…
}
{\displaystyle O_{x_{0}}=\{\ldots ,\ f^{-2}(x_{0}),\ f^{-1}(x_{0}),\ x_{0},\ f(x_{0}),\ f^{2}(x_{0}),\ \ldots \}}
其中指數指的是函數f 與自身複合的次數。注意
O
x
0
=
O
f
(
x
0
)
=
O
f
−
2
(
x
0
)
,
e
t
c
.
{\displaystyle O_{x_{0}}=O_{f(x_{0})}=O_{f^{-2}(x_{0})},\ {\rm {etc.}}}
F
1
,
x
0
{\displaystyle F_{1,\ x_{0}}}
F
1
{\displaystyle {\mathcal {F}}_{1}}
f 的動力學。若流形X 已經葉化,則只要f 是葉間映射,就可以利用這構造增加葉狀結構的余維數。
2-環面的克羅內克葉狀結構是旋轉
R
α
:
S
1
→
S
1
{\displaystyle R_{\alpha }:\ S^{1}\to S^{1}}
α
∈
[
0
,
2
π
)
{\displaystyle \alpha \in [0,\ 2\pi )}
切割重粘後,2-洞環面的緯懸。 a) 帶待切割截面的雙洞環面; b) 切割後帶有4個面的幾何圖形。 更具體地說,若
Σ
=
Σ
2
{\displaystyle \Sigma =\Sigma _{2}}
C
1
,
C
2
∈
Σ
{\displaystyle C^{1},\ C^{2}\in \Sigma }
F
{\displaystyle {\mathcal {F}}}
Σ
×
{
y
}
,
y
∈
S
1
{\displaystyle \Sigma \times \{y\},\ y\in S^{1}}
M
=
Σ
×
S
1
{\displaystyle M=\Sigma \times S^{1}}
N
i
=
C
i
×
S
1
{\displaystyle N_{i}=C_{i}\times S^{1}}
F
{\displaystyle {\mathcal {F}}}
N
i
,
i
=
1
,
2
{\displaystyle N_{i},\ i=1,\ 2}
D
i
f
f
+
(
S
1
)
{\displaystyle {\rm {Diff}}_{+}(S^{1})}
S
1
{\displaystyle S^{1}}
f
1
,
f
2
∈
D
i
f
f
+
(
S
1
)
{\displaystyle f_{1},\ f_{2}\in {\rm {Diff}}_{+}(S^{1})}
M 沿
N
1
,
N
2
{\displaystyle N_{1},\ N_{2}}
N
i
+
,
N
i
−
{\displaystyle N_{i}^{+},\ N_{i}^{-}}
M
′
=
Σ
′
×
S
1
{\displaystyle M'=\Sigma '\times S_{1}}
{
N
i
±
}
i
=
1
,
2
.
{\displaystyle \left\{N_{i}^{\pm }\right\}_{i=1,2}.}
F
{\displaystyle {\mathcal {F}}}
∂
M
′
{\displaystyle \partial M'}
F
′
{\displaystyle {\mathcal {F^{\prime }}}}
Σ
′
×
{
y
}
,
y
∈
S
1
{\displaystyle \Sigma '\times \{y\},\ y\in S^{1}}
這片葉在4個圓
C
i
±
×
{
y
}
⊂
N
i
±
{\displaystyle C_{i}^{\pm }\times \{y\}\subset N_{i}^{\pm }}
∂
M
′
{\displaystyle \partial M'}
z
∈
C
i
{\displaystyle z\in C_{i}}
C
i
±
{\displaystyle C_{i}^{\pm }}
z
±
{\displaystyle z^{\pm }}
N
i
−
{\displaystyle N_{i}^{-}}
N
i
+
{\displaystyle N_{i}^{+}}
(
z
−
,
y
)
≡
(
z
+
,
f
i
(
y
)
)
,
i
=
1
,
2.
{\displaystyle (z^{-},y)\equiv (z^{+},f_{i}(y)),\quad i=1,2.}
由於
f
1
,
f
2
{\displaystyle f_{1},\ f_{2}}
S
1
{\displaystyle S^{1}}
M 。
F
′
{\displaystyle {\mathcal {F^{\prime }}}}
M 新的葉狀結構
F
(
f
1
,
f
2
)
{\displaystyle {\mathcal {F}}(f_{1},\ f_{2})}
F
(
f
1
,
f
2
)
{\displaystyle {\mathcal {F}}(f_{1},\ f_{2})}
L 包含一片
Σ
′
×
{
y
0
}
{\displaystyle \Sigma '\times \{y_{0}\}}
L
=
⋃
g
∈
G
Σ
′
×
{
g
(
y
0
)
}
,
{\displaystyle L=\bigcup _{g\in G}\Sigma ^{\prime }\times \{g(y_{0})\},}
其中
G
⊂
D
i
f
f
+
(
S
1
)
{\displaystyle G\subset {\rm {Diff}}_{+}(S^{1})}
{
f
1
,
f
2
}
{\displaystyle \{f_{1},\ f_{2}\}}
∀
z
∈
C
1
,
(
z
−
,
g
(
y
0
)
)
≡
(
z
+
,
f
1
(
g
(
y
0
)
)
)
{\displaystyle \forall z\in C_{1},\ (z^{-},\ g(y_{0}))\equiv (z^{+},\ f_{1}(g(y_{0})))}
∀
z
∈
C
2
,
(
z
−
,
g
(
y
0
)
)
≡
(
z
+
,
f
2
(
g
(
y
0
)
)
)
{\displaystyle \forall z\in C_{2},\ (z^{-},\ g(y_{0}))\equiv (z^{+},\ f_{2}(g(y_{0})))}
其中g 在G 上取值。葉完全由
y
0
∈
S
1
{\displaystyle y_{0}\in S^{1}}
G -軌道決定,可以很簡單也可以很複雜。例如若相應的G -軌道有限,則葉就是緊的。舉個極端的例子,若G 是平凡的
(
f
1
=
f
2
=
i
d
S
1
)
{\displaystyle (f_{1}=f_{2}={\rm {id}}_{S^{1}})}
F
(
f
1
,
f
2
)
=
F
{\displaystyle {\mathcal {F}}(f_{1},\ f_{2})={\mathcal {F}}}
S
1
{\displaystyle S^{1}}
M 中也稠密。例如,若
f
1
,
f
2
{\displaystyle f_{1},\ f_{2}}
L 的閉包
L
¯
{\displaystyle {\bar {L}}}
{
w
}
×
S
1
{\displaystyle \{w\}\times S^{1}}
康托爾集 中相遇。在
Σ
×
I
{\displaystyle \Sigma \times I}
I 是緊非退化區間。這裏,取
f
1
,
f
2
∈
D
i
f
f
+
(
I
)
{\displaystyle f_{1},\ f_{2}\in {\rm {Diff}}_{+}(I)}
∂
I
{\displaystyle \partial I}
∂
M
{\displaystyle \partial M}
M' ,就會得到有角葉狀流形。無論哪種情形,這種構造都被稱作微分同胚對的緯懸,提供了余維為1的葉狀結構的有趣例子。
假設一切都光滑 ,那麼向量場 之間有一種密切關係:給定M 上不為零的向量場X ,其積分曲線 將給出1維葉狀結構(即余維為n -1的葉狀結構)。
這觀察可推廣為弗羅貝尼烏斯定理 ,即分佈(流形切叢 的n − p 維子叢 )與葉狀結構的葉相切的充分必要條件 是,與分佈相切的向量場集對李括號 閉合。這也可以解釋為,將切叢 的結構群從
G
L
(
n
)
{\displaystyle {\rm {GL}}(n)}
弗羅貝尼烏斯定理中的條件作為可積條件 出現,並斷言若滿足條件,就能約化,因為具有所需塊結構的局部轉移函數存在。例如,對某(非規範)
α
∈
Ω
1
{\displaystyle \alpha \in \Omega ^{1}}
k
e
r
(
α
)
{\displaystyle {\rm {ker}}(\alpha )}
α
∧
d
α
=
0
{\displaystyle \alpha \wedge {\rm {d}}\alpha =0}
由於存在拓撲約束,因此存在全局葉狀結構理論。例如,曲面 情形中,處處非零向量場只能存在於環面 的有向 緊 曲面上。這是龐加萊-霍普夫定理 的結果,指出歐拉示性數 需為0。其與切觸幾何 有很多深層聯繫,專門研究不可積情形。
Haefliger (1970) 給出連通非緊流形上的分佈與可積分佈同倫的充分必要條件。Thurston (1974 , 1976 ) 證明,任意有分佈的緊流形都有同維度的葉狀結構。
Anosov, D.V., Foliation , Hazewinkel, Michiel (編), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 Candel, Alberto; Conlon, Lawrence. Foliations I. Graduate Studies in Mathematics 23 . Providence, Rhode Island: American Mathematical Society . 2000. ISBN 0-8218-0809-5 Candel, Alberto; Conlon, Lawrence. Foliations II. Graduate Studies in Mathematics 60 . Providence, Rhode Island: American Mathematical Society . 2003. ISBN 0-8218-0809-5 Gourgoulhon, Éric. 3+1 Formalism in General Relativity . Lecture Notes in Physics 846 . Heidelberg, New York, Dordrecht, London: Springer . 2012 [2024-01-05 ] . ISBN 978-3-642-24524-4doi:10.1007/978-3-642-24525-1 存檔 於2023-09-22). Haefliger, André, Feuilletages sur les variétés ouvertes, Topology , 1970, 9 (2): 183–194, ISSN 0040-9383 MR 0263104 doi:10.1016/0040-9383(70)90040-6 Lawson, H. Blaine, Foliations , Bulletin of the American Mathematical Society , 1974, 80 (3): 369–418, ISSN 0002-9904 MR 0343289 doi:10.1090/S0002-9904-1974-13432-4 Moerdijk, Ieke ; Mrčun, J., Introduction to foliations and Lie groupoids, Cambridge Studies in Advanced Mathematics 91 , Cambridge University Press , 2003, ISBN 978-0-521-83197-0MR 2012261 Reeb, Georges, Sur certaines propriétés topologiques des variétés feuilletées, Actualités Sci. Ind., no. 1183, Hermann & Cie., Paris, 1952, MR 0055692 Thurston, William, The theory of foliations of codimension greater than one , Commentarii Mathematici Helvetici , 1974, 49 : 214–231, ISSN 0010-2571 MR 0370619 S2CID 120603728 doi:10.1007/BF02566730 [失效連結 Thurston, William P. , Existence of codimension-one foliations, Annals of Mathematics , Second Series, 1976, 104 (2): 249–268, ISSN 0003-486X JSTOR 1971047 MR 0425985 doi:10.2307/1971047





 . (原始內容存檔 (PDF)於2024-01-05).
. (原始內容存檔 (PDF)於2024-01-05).











![{\displaystyle (a,\ 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ef48efee9998eadda860f99a12edaf2b594168f)

















































































































































































































































![{\displaystyle [s]\in \pi _{1}(S^{1},\ x_{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b516404aa48d688c699c563317a0902c223cb4b)

























































![{\displaystyle {\begin{cases}f:[-1,1]\times \mathbb {R} \to \mathbb {R} \\f(x,y)=(x^{2}-1)e^{y}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2485598c9933fa847e7482b4eff219cbd71fc65)
![{\displaystyle [-1,\ 1]\times \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/71b16bdd3f4a8a21518c977a6c28044de282c6d4)


![{\displaystyle (x,\ y)\in [-1,\ 1]\times \mathbb {R} ,\ n\in \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/51be7434f8ce09604f883008aed425d8e583ceb6)
![{\displaystyle \mathbb {Z} \backslash ([-1,\ 1]\times \mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d87c709607aeccc578bb47d4aff374d151239107)

![{\displaystyle (r,\ \theta )\in [0,\ 1]\times S^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/619acaa9fce55722e336fbb41a08666960ee0725)
















































![{\displaystyle [0,\ 1]\times X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba718d67570e42cdec7e772a2fb0ef9a7ba12e6a)

![{\displaystyle M=S^{1}\times _{f}X=[0,\ 1]\times X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5352287cce10d492ee7216da00ab0f7c8e17f7be)



![{\displaystyle F_{2,\ x_{0}}=\{(t,\ x):\ t\in [0,\ 1],\ x\in O_{x_{0}}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbc010b3073ee4945478dafefa1cd4cd89218ef9)
















































