二進位

記數系統
印度-阿拉伯數字系統
西方阿拉伯數字 阿拉伯文數字 高棉數字 孟加拉數字	印度數字 波羅米數字 泰語數字
漢字文化圈記數系統
中文數字 閩南語數字 越南語數字 算籌	日語數字 韓語數字 蘇州碼子
字母記數系統
阿拉伯字母數字 亞美尼亞數字 西里爾數字 吉茲數字	希伯來數字 希臘數字 阿利耶波多數字
其它記數系統
雅典數字 巴比倫數字 古埃及數字 伊特拉斯坎數字	瑪雅數字 羅馬數字 熙篤會數字 卡克托維克數字
依底數區分的進位制系統
1 2 3 4 5 6 8 9 10 11 12 15 16 18 20 24 30 32 36 60 64

二進制（binary）在數學和數位電路中指以2為底數的記數系統，以2為基數代表系統是二進位制的。這一系統中，通常用兩個不同的數字0和1來表示。數字電子電路中，邏輯閘直接採用了二進制，因此現代的計算機和依賴計算機的裝置裡都用到二進制。每個數字稱為一個位元（二進制位）或位元（Bit，Binary digit 的縮寫）。

歷史

現代的二進位記數系統由戈特弗里德·萊布尼茨於1679年設計，在他1703年發表的文章《論只使用符號0和1的二進位算術，兼論其用途及它賦予伏羲所使用的古老圖形的意義》出現。與二進位數相關的系統在一些更早的文化中也有出現，包括古埃及、古代中國、古印度以及太平洋島原住民文明。其中，古代中國的《易經》尤其引起了萊布尼茨的聯想。

　

荷魯斯之眼各部分所代表的算術值

埃及

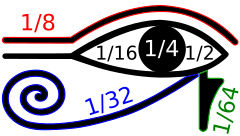
古埃及的計數員使用兩種不同的系統表示分數，一是埃及分數（與二進位記數系統無關），二是荷魯斯之眼分數（叫這個名字是因為很多數學史家相信這個系統所採用的符號可以排列成荷魯斯之眼，但這一點有爭議）。荷魯斯之眼分數是用來表示分數數量的穀物、液體等的二進位記數系統，在這一系統下，以赫卡特為單位的分數值表示成1/2、1/4、1/8、1/16、1/32和1/64等二進位分數的和。 這一系統的早期形式可以在埃及第五王朝（約公元前2400年）的檔案中找到，而發展完備的象形文字形式可追溯到埃及第十九王朝（約公元前1200年）。 古埃及做乘法的方式也與二進位數密切相關，約公元前1650年的萊因德數學紙草書中就能看到。這一計算方法中，要把1和乘數不斷翻倍，按被乘數的二進位表示從左列選出相應的2的冪次，並將右列的數相加。

印度

印度學者平甲拉（公元前兩世紀左右）通過二進位方法來研究韻律詩。他的二進位中用到的是長短音節（一個長音節相當於兩個短音節），有些像摩爾斯電碼。與西方的位置表示法不同，平甲拉的系統中，二進位是從右往左書寫的。

太平洋島原住民文明

在法屬玻里尼西亞的曼格雷哇島，挪威卑爾根大學的人類學家Andrea Bender和Sieghard Beller發現，在曼格雷哇人的語言上，存在著一個似乎混合了十進位和二進位的數學系統。它先於西方幾個世紀，為首個在歐亞大陸之外發展出的二進位演算法 。

萊布尼茨前的西方先驅

1605年，弗朗西斯·培根提出了一套系統，可以把26個字母化為二進位數。此外他補充道，這個思路可以用於任何事物：「只要這些事物的差異是簡單對立的，比如鈴鐺和喇叭，燈光和手電筒，以及火槍和類似武器的射擊聲」。這對二進位編碼的一般理論有重要意義。（參見培根密碼）

萊布尼茨和中國的《易經》

戈特弗里德·萊布尼茲

萊布尼茨關於二進位的論文全名是《論只使用符號0和1的二進位算術，兼論其用途及它賦予伏羲所使用的古老圖形的意義》（1703年）。類似於現代二進位計數系統，萊布尼茲的系統使用0和1。下面是萊布尼茲的二進位記數系統的一個例子：

• 0 0 0 1 數值為$2^{0}$
• 0 0 1 0 數值為$2^{1}$
• 0 1 0 0 數值為$2^{2}$
• 1 0 0 0 數值為$2^{3}$

萊布尼茲認為易經中的卦象與二進位算術密不可分。萊布尼茲解讀了易經中的卦象，並認為這是其作為二進位算術的證據。作為親華派，萊布尼茲關注易經，並饒有興致地注意到它的卦象與從0到111111的二進位數位有某種對應，並認為這種對應反映了中國的重大成就中展現的他所崇尚的數學哲學。萊布尼茲首次接觸到易經是在與法國耶穌會傳教士白晉的聯絡中。白晉1685年作為傳教士前往中國。 長期以來，人們對萊布尼茨發明二進位是否受到了伏羲八卦的影響爭議頗多。認為萊布尼茨未受伏羲八卦影響獨立發明二進位的理由主要是萊布尼茨在1679年（與白晉首次通訊的二十多年）就撰寫了「二的級數」（De Progressione Dyadica）一文；而目前有學者傾向於認為萊布尼茨二進位的體系確源於伏羲八卦圖，原因在於1687年萊布尼茨看過柏應理的《這個哲學家孔子》，書中便有伏羲八卦次序圖、方點陣圖和周文王六十四卦圖。此外，萊布尼茨還閱讀過1660年斯比賽爾出版的《中國文史評析》，其中亦有對《易經》和八卦的介紹。 此外，萊布尼茲認為易經的卦象肯定了他所信仰的基督教的共相。一切數都可以用0和1創造出來，在萊布尼茲看來，這正象徵了基督教《聖經》所說的上帝從「無」創造「有」（creatio ex nihilo）。

（有一個概念）不容易傳授給異教徒：全能的上帝從無創造有。現在我們可以說，數位的起源是世上能最好展示和說明這種力量的事物，它以「一」和「零」或者說「無」的形式呈現，既樸素又簡練。

——萊布尼茨寫給魯道夫·奧古斯都公爵的信

後來的發展

喬治·布爾

1854年，英國數學家喬治·布爾發表了一篇里程碑式的論文，其中詳細介紹了一種代數化的邏輯系統，後人稱之為布林代數。他提出的邏輯演算在後來的電子電路設計中起基礎性作用。

1937年，克勞德·夏農在麻省理工大學完成了其電機工程碩士學位論文，用繼電器和開關實現了布林代數和二進位算術運算。論文題為《繼電器與開關電路的符號分析》（A Symbolic Analysis of Relay and Switching Circuits），其中夏農的理論奠定了數位電路的理論基礎。夏農憑這篇論文於1940年被授予美國阿爾弗雷德·諾貝爾協會美國工程師獎。哈佛大學的哈沃德·加德納稱，夏農的碩士論文「可能是本世紀最重要、最著名的碩士學位論文」。

1937年11月，任職於貝爾實驗室的喬治·斯蒂比茲發明了用繼電器表示二進位的裝置。它是第一台二進位電腦。

運算規則

四則運算

• 加法：0+0＝0，0+1＝1，1+0＝1，1+1＝10
• 減法：0－0＝0，1－0＝1，1－1＝0，10－1＝1
• 乘法：0×0＝0，0×1＝0，1×0＝0，1×1＝1
• 除法：0÷1＝0，1÷1＝1

拈加法

主條目：邏輯互斥或和拈

二進制的一種特殊的演算法，稱為拈加法。進行拈加法時，與進行加法無異，只是不需進行進位，即是逐位XOR。與博弈論的關係，見尼姆遊戲 § 數學理論。

不同進位數轉換

十進位化為二進位

整數部分，把十進位轉成二進位一直分解至商數為0。讀餘數從下讀到上，即是二進位的整數部分數字。

小數部分，則用其乘2，取其整數部分的結果，再用計算後的小數部分依此重複計算，算到小數部分全為0為止，之後讀所有計算後整數部分的數位，從上讀到下。

將59.25₍₁₀₎ 轉成二進制：

1. 整數部分：

   59 ÷ 2 = 29 ... 1
   29 ÷ 2 = 14 ... 1
   14 ÷ 2 =  7 ... 0
    7 ÷ 2 =  3 ... 1
    3 ÷ 2 =  1 ... 1
    1 ÷ 2 =  0 ... 1
   

2. 小數部分：

   0.25 × 2 = 0.5 ... 0
   0.50 × 2 = 1.0 ... 1
   

所以：$59.25_{(10)}=111011.01_{(2)}$

也可以公式來計算：

           59.2510 = 101*10101+1001*10100+10*1010-1+101*1010-2
                   = 101*1010+1001+10/1010+101/1010/1010
                   = 110010+1001+(10+0.1)/1010
                   = 111011+0.01
                   = 111011.01

二進位化為十進位

將100101₂轉換為十進位形式如下：

100101₂ = [ ( 1 ) × 2⁵ ] + [ ( 0 ) × 2⁴ ] + [ ( 0 ) × 2³ ] + [ ( 1 ) × 2² ] + [ ( 0 ) × 2 ] + [ ( 1 ) × 1 ]

100101₂ = [ 1 × 32 ] + [ 0 × 16 ] + [ 0 × 8 ] + [ 1 × 4 ] + [ 0 × 2 ] + [ 1 × 1 ]

100101₂ = 37₁₀

十進制	0	1	2	3	4	5	6	7	8	9	10
二進制	0	1	10	11	100	101	110	111	1000	1001	1010
十進制	11	12	13	14	15	16	17	18	19	20	21
二進制	1011	1100	1101	1110	1111	10000	10001	10010	10011	10100	10101
十進制	22	23	24	25	26	27	28	29	30	31	32
二進制	10110	10111	11000	11001	11010	11011	11100	11101	11110	11111	100000
十進制	33	34	35	36	37	38	39	40	41	42	43
二進制	100001	100010	100011	100100	100101	100110	100111	101000	101001	101010	101011

二進位化為八進位

把二進位化為八進位也不是很難，因為八進位以8為基數，8是2的冪（8=2³），因此八進位的一位恰好需要三個位元來表示。八進位與二進位數之間的對應就是上面表格中十六進位的前八個數。二進位數000就是八進位數0，二進位數111就是八進位數7，以此類推。

八進位	二進位
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

八進位轉為二進位：

• 65₈ = 110 101₂
• 17₈ = 001 111₂

二進位轉八進位：

• 101100₂ = 101 100₂ （三位一組） = 54₈
• 10011₂ = 010 011₂ （用零填充 (密碼學)，三位一組） = 23₈

八進位化為十進位

遵循二進位化為十進位的方法即可。所不同的是每一位乘上一個底數為8的冪。

• 65₈ = (6 × 8¹) + (5 × 8⁰) = (6 × 8) + (5 × 1) = 53₁₀
• 127₈ = (1 × 8²) + (2 × 8¹) + (7 × 8⁰) = (1 × 64) + (2 × 8) + (7 × 1) = 87₁₀

表示實數

非整數可以借負指數冪表示；只要用基數點（十進位中，就是小數點）把負指數冪表示的部分隔開即可。例如，二進位數11.01₂：

1 × 21	(1 × 2 = 2)	加
1 × 20	(1 × 1 = 1)	加
0 × 2−1	(0 × 1⁄2 = 0)	加
1 × 2−2	(1 × 1⁄4 = 0.25)

就是十進位數位3.25。

所有二進分數${\frac {p}{2^{a}}}$都對應一個「有窮」二進位數位——這一二進位表示的小數部分位數有限。其他有理數也有二進位表示，但不是有窮的，而是出現迴圈，即某個有限序列出現無數次。例如

${\frac {1_{10}}{3_{10}}}$ = ${\frac {1_{2}}{11_{2}}}$ = 0.0101010101…₂

${\frac {12_{10}}{17_{10}}}$ = ${\frac {1100_{2}}{10001_{2}}}$ = 0.10110100 10110100 10110100...₂

在其他基數的計數系統中，有理數的表示也是有窮或迴圈的。另一相似之處在於，如果我們有一個有窮表示，那麼它還會有其他的表示方式，例如幾何級數2⁻¹ + 2⁻² + 2⁻³ + ...的和既是1，也是0.111111...。

無限不迴圈二進位小數表示的是無理數。例如，

• 0.101001000100001000001000000…有某種模式，但迴圈節長度不固定，所以是無理數。這個數的數值為$2^{-{\tfrac {7}{8}}}\theta _{2}\left(0;{\tfrac {\sqrt {2}}{2}}\right)-1\approx 0.64163256...$，其中$\theta _{2}$為Θ函式。
• 1.0110101000001001111001100110011111110…是2的平方根${\sqrt {2}}$的二進位表示，也是一個無理數。它沒有可以看出的模式。參見無理數。