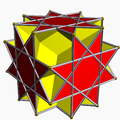
小斜方立方體
 | ||||
| 類別 | 均勻星形多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 小反平行四邊形二十四面體 | |||
| 識別 | ||||
| 名稱 | 小斜方立方體 Small rhombihexahedron | |||
| 別名 | 小斜方六面體 | |||
| 參考索引 | U18, C60, W86 | |||
| 鮑爾斯縮寫 | sroh | |||
| 數學表示法 | ||||
| 威佐夫符號 | 2 4 (3/2 4/2) | | |||
| 性質 | ||||
| 面 | 18 | |||
| 邊 | 48 | |||
| 頂點 | 24 | |||
| 歐拉特徵數 | F=18, E=48, V=24 (χ=-6) | |||
| 組成與佈局 | ||||
| 面的種類 | 12個正方形 6個八邊形 | |||
| 頂點圖 | 4.8.4/3.8/7 | |||
| 對稱性 | ||||
| 對稱群 | Oh, [4,3], (*432) | |||
| 圖像 | ||||
| ||||
小斜方立方體是一種均勻多面體[1],由12個正方形和6個八邊形組成[2],其外觀與小立方立方八面體十分相似,差別在小立方立方八面體的凹陷處在小斜方立方體中是面,而小立方立方八面體的面在小斜方立方體中是凹陷處。[3]:134小斜方立方體最早出現在1881年由亞伯特·巴杜羅(Albert Badoureau)描述的6種半擬正多面體(Versi-Quasi-Regular Polyhedra)中[4]。後來又被考克斯特和米勒於1930年到1932年間發現並命名。[5]此外,小斜方立方體可以視為小斜方截半立方體經過刻面後的結果[6],同時,其凸包也為小斜方截半立方體。[7]
命名
[編輯]在名稱中,小斜方立方體的「斜方」(Rhombi-)是指菱形,表示這個多面體有12個面分別與菱形十二面體的12個面平行,這12個面為正方形;小斜方立方體的立方體(-hexahedron)則代表這個立體有6個面分別與立方體(又稱六面體)的6個面平行,這6個面在小斜方立方體中為正八邊形。[8]
性質
[編輯]小斜方立方體由18個面、48條邊和24個頂點組成[8][2][9],其中24個頂點互相交叉連結交,沒有交叉連結的部分構成了小斜方立方體的12個正方形面,[10]並且這12個正方形面分別與菱形十二面體的12個菱形面平行[8];剩下的交叉連結的頂點構成了6個八邊形,這6個八邊形面分別與立方體的6個正方形面平行。[8]同時,這24個頂點具有點可遞的特性,這意味著,這立體上的任意兩個頂角A和B,透過旋轉或鏡射這個立體,使A移動到B原來的位置時,其頂角以及其二面角仍然佔據了相同的空間區域[11],也代表著這個立體是一個等角立體。小斜方立方體每個頂點都是2個八邊形和2個正方形的公共頂點,並具有交叉梯形的頂點圖[11]在頂點布局中,可以用{8, 4, 8/7, 4/3}來表示[9][12]。若將這個立體視為簡單多面體,則其由66個面組成[8]
定向性
[編輯]小斜方立方體的表面是一個不可定向的曲面[9],即無法定義表面上特定點屬於內部或外部,因為任何點都可以在不打洞的情況下經由表面找到一個路徑連接該點對應的背面的位置,這個特性與克萊因瓶類似[11]。
尺寸
[編輯]若小斜方立方體的邊長為單位長,則其外接球半徑為:[6]
二面角
[編輯]小斜方立方體有兩種二面角,分別為45度和90度,這兩種二面角所對應的稜各24條。[13]其中直角位於三角形凹洞中、45度角位於正方形凹洞中。[7]
相關多面體
[編輯]小斜方立方體與星形截角立方體共用相同的頂點布局[14],其亦與大斜方立方體、小立方立方八面體和小斜方截半立方體有著相同的稜布局。[7]
-
小斜方立方體
小斜方立方體與大斜方立方體拓樸同構,其可以透過替換八邊形與八角星來轉變為另一個立體。[7][15]
-
小斜方立方體
參見
[編輯]參考文獻
[編輯]- ^ Wolfram, Stephen. "Small Rhombihexahedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英語).
- ^ 2.0 2.1 Vladimir Bulatov. small rhombihexahedron. Polyhedra Collection. [2021-09-12]. (原始內容存檔於2021-09-03).
- ^ Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. (原始內容存檔於2021-08-31).
- ^ Jean Paul Albert Badoureau. Mémoire sur les Figures Isocèles. Journal de l'École polytechnique. 1881, (49): 47-172.
- ^ H. S. M. Coxeter; M. S. Longuet-Higgins; J. C. P. Miller. Uniform Polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 1954, 246: 401–450.
- ^ 6.0 6.1 Weisstein, Eric W. (編). Small Rhombihexahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ 7.0 7.1 7.2 7.3 Klitzing, Richard. small rhombihexahedron, sroh. bendwavy.org. [2021-09-12]. (原始內容存檔於2021-08-09).
- ^ 8.0 8.1 8.2 8.3 8.4 Robert Webb. Small Rhombihexahedron. software3d.com. [2021-09-12]. (原始內容存檔於2021-03-02).
- ^ 9.0 9.1 9.2 Roman E. Maeder. 18: small rhombihexahedron. mathconsult.ch. 1997 [2021-09-12]. (原始內容存檔於2020-02-17).
- ^ Wenge Qiu, Jason A. Perman, Łukasz Wojtas, Mohamed Eddaoudi, Michael J. Zaworotko. Structural diversity through ligand flexibility: two novel metal–organic nets via ligand-to-ligand cross-linking of “paddlewheels”. Chemical Communications. 2010, 46 (46): 8734 [2021-09-12]. ISSN 1359-7345. doi:10.1039/c0cc03270k (英語).
- ^ 11.0 11.1 11.2 David I. McCooey. Versi-Quasi-Regular Polyhedra. dmccooey.com. [2021-09-05]. (原始內容存檔於2020-06-18).
- ^ Paul Bourke. Uniform Polyhedra. paulbourke.net. October 2004 [2021-09-12]. (原始內容存檔於2013-09-02).
- ^ David I. McCooey. Versi-Quasi-Regular Polyhedra : Small Rhombihexahedron. dmccooey.com. [2021-09-05]. (原始內容存檔於2021-09-03).
- ^ Klitzing, Richard. stellated truncated hexahedron, quith. bendwavy.org. [2021-09-12]. (原始內容存檔於2021-08-09).
- ^ Klitzing, Richard. great rhombihexahedron : groh. bendwavy.org. [2021-09-05]. (原始內容存檔於2021-08-09).