簡諧運動
簡諧運動,或稱簡諧振動、諧振、SHM(Simple Harmonic Motion),即是最基本也是最簡單的一種機械振動。當某物體進行簡諧運動時,物體所受的力(或物體的加速度)的大小與位移的大小成正比,並且力(或物體的加速度)總是指向平衡位置。
如果用表示物體受到的回復力,用表示物體對於平衡位置的位移,根據虎克定律,和成正比,它們之間的關係可用下式來表示:
式中的是回復力與位移成正比的比例係數;負號的意思是:回復力的方向總跟物體位移的方向相反。
根據牛頓第二運動定律「」當物體質量一定時,運動物體的加速度總跟物體所受淨力的大小成正比,跟淨力的方向相同,且系統的機械能守恆。
動力學方程式
[編輯]
對於一維的簡諧振動,其動力學方程式是二階微分方程式,可由牛頓第二運動定律得到
回復力又可表示為
所以有
求解上述方程式,得到的解含有正弦函數
- ,其中
,是由初始條件決定的常數。取平衡位置為原點,每項都有物理意義:是振幅,是角頻率, 加速度可以作為時間的函數得到
- (在平衡位置)
- (在最大位移處)
加速度也可以通過位移的函數得到
- 。
因為 ,
- ,
又因為週期 ,所以:。
以上方程式說明了簡諧振動具有等時性,即一個做簡諧振動的質點運動週期和振幅以及相位無關。[1]:163
線性回復力
[編輯]在運動過程中,物體所受力的大小與它的位移的大小成正比,而力的方向與位移的方向相反。具有這種性質的力稱為線性回復力。
彈簧
[編輯]將一個有孔小球體與一個彈簧連在一在運動過程中,物體所受力的大小與它的位移的大小成正比,而力的方向與位移的方向相反。具有這種性質的力稱為線性回復力。平杆穿入小球體,使球體可以在水平杆上左右滑動,而球體與水平杆的摩擦力小得可以忽略不計。將彈簧的一端固定住,彈簧的整體質量要比球體質量小得多,這樣彈簧本身質量也可以忽略不計。這個系統便是一個彈簧振子。
彈簧振子系統在平衡狀態下,彈簧沒有形變,振子(小球體)在平衡位置保持靜止。若把振子拉過平衡位置,到達最大幅度,再鬆開,彈簧則會將振子向平衡位置收回。在收回的過程中,彈簧的位能轉換為振子的動能,位能在降低的同時,動能在增加。當振子到達平衡位置時,振子所積累的動能又迫使振子越過平衡位置,繼續向同樣的方向移動。但因已越過彈簧振子系統的平衡位置,所以這時彈簧開始對振子向相反方向施加力。動能轉作位能,動能降低,位能上升,直至到達離平衡位置最大幅度的距離。這時振子所有的動能被轉化為位能,振子速度為零,停止運動。位能又迫使振子移回平衡位置,在移動過程中,位能轉為動能,因而再次越過平衡位置,重複這個過程。在沒有任何其他力影響的完美的條件下,這個彈簧振子系統會在兩個最大幅度點間不停地做往返運動。彈簧振子的固有週期和固有頻率與彈簧彈力係數和振子質量有關,與振幅大小無關。
振幅、週期和頻率
[編輯]1.振幅
振幅代表質點偏離中心(平衡位置)的最大距離,它正比於,即它的平方正比於系統的機械能E。
2.角頻率
角頻率:, 頻率f為週期T的倒數。
其中。推導過程:
- 對於時間t求導,
- 再關於時間t求導,
- 由牛頓第二運動定律得
- 兩式聯立得。
下圖為簡諧運動的圖像,表示的是振動物體的位移隨時間變化的規律。是一條正弦或餘弦曲綫。
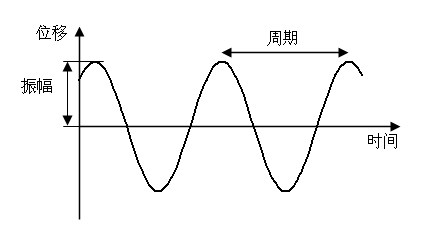
這個運動是假設在沒有能量損失引致阻尼的情況而發生。振幅描繪了振動的強弱,是標量,大小為最大位移的大小,質點在一次全振動過程中通過的路程等於4倍振幅。完成一次全振動的時間叫週期,單位時間內完成全振動的次數叫頻率,週期和頻率描繪了振動的快慢。
簡諧振動的判定
[編輯]- 如果一個質點在運動中所受的淨外力是一個簡諧力
- 如果一個質點的運動方程式有如下形式
- 如果一個質點的動力學方程式可以寫成
- 如果質點在運動過程中具有形式為的彈力位能,且
應該說明:
- 以上各判定方法是完全等價的;
- 以上各表達式中的既可以是線量(線位移),又可以是角量(角位移),相應的,速度可以為線速度和角速度,對應的加速度是線加速度和角加速度。
例子
[編輯]彈簧
[編輯]把質量為的物體懸掛在彈力常數為k的彈簧的底端,則物體將進行簡諧運動,其方程式為:
如果要計算它的週期,可以用以下的公式:
- 。
總能量是常數,由方程式給出。
等速率圓周運動
[編輯]等速率圓周運動的一維投影是簡諧運動。如果物體以的角速率沿著半徑為的圓移動,則它在x軸、y軸或任意一條直徑上的投影會是簡諧運動,其振幅為,角速率為。
在偏角不太大的情況(一般認為小於5°)下,單擺的運動可以近似地視為簡諧運動。如果單擺的長度為,重力加速度為,則週期為:
這個公式僅當偏角很小時才成立,因為角加速度的表達式是與位置的正弦成正比的:
其中I是轉動慣量,在這種情況下。當很小時,,因此上式變為:
這使得角加速度與成正比,滿足了簡諧運動的定義。單擺的回復力是擺球的重力沿運動方向的分力。[1]:165
參閱
[編輯]參考資料
[編輯]- ^ 1.0 1.1 1.2 趙志敏. 高中教程。基础篇. 復旦大學出版社. 2011年10月. ISBN 978-7-309-08251-7 (中文(中國大陸)).
外部連結
[編輯]- 彈簧震動Java模擬 (頁面存檔備份,存於網際網路檔案館)
| ||||||||||||||
















































