跳转到内容

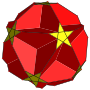
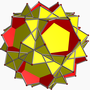
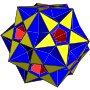
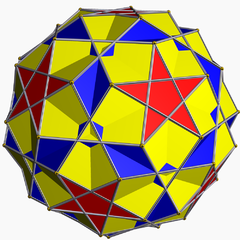
斜方截半大十二面体

本页使用了标题或全文手工转换
维基百科，自由的百科全书
  提示：此条目页的主题不是大斜方截半十二面体。
斜方截半大十二面体
斜方截半大十二面体
类别星形均匀多面体
对偶多面体中鸢形六十面体（英语：Medial deltoidal hexecontahedron）在维基数据编辑
识别
名称斜方截半大十二面体
参考索引U38, C48, W76
鲍尔斯缩写
（verse-and-dimensions的wikia：Bowers acronym）		raded在维基数据编辑
数学表示法
考克斯特符号
（英语：Coxeter-Dynkin diagram）		node_1 5 rat d2 node 5 node_1 
施莱夫利符号t0,2{5/2,5}
威佐夫符号
（英语：Wythoff symbol）		5/2 5 | 2
性质
面54
边120
顶点60
欧拉特征数F=54, E=120, V=60 （χ=-6）
组成与布局
面的种类30个正方形
12个五角星
12个五边形[1]
面的布局
（英语：Face configuration）		30{4}+12{5}+12{5/2}
顶点图4.5/2.4.5
对称性
对称群Ih, [5,3], *532
特性
顶点正、非凸
图像

4.5/2.4.5
（顶点图）

中鸢形六十面体（英语：Medial deltoidal hexecontahedron）
（对偶多面体）

在几何学中，斜方截半大十二面体是一种星形均匀多面体，由12个五角星、30个正方形和12个正五边形组成[1]，其可以视为小星形十二面体透过离面（Cantellation）或扩展（Expansion）变换而成[注 1]，温尼尔在他的书《多面体模型》中列出许多星形多面体模型，其中也收录了此种形状，并给予编号W76[5]。斜方截半大十二面体每个顶点都是4个多边形形成的四面角，因此对应的对偶多面体为由四边形构成的中鸢形六十面体（英语：Medial deltoidal hexecontahedron）。

性质

[编辑]

斜方截半大十二面体由54个面、120条边和60个顶点组成[6]在施莱夫利符号中可以用rr{5/2,5}表示[2]，而施莱夫利符号rr表示离面（Cantellation）变换[4]，该变换施莱夫利符号中也可以计为t0,2[7]，该变换与正二十面体变换成小斜方截半二十面体的变换相同，因此斜方截半大十二面体在施莱夫利符号中也可以计为t0,2{5/2,5}，此表示法对应到的威佐夫布局为5/2 5 | 2[6]。

面的组成

[编辑]

斜方截半大十二面体由12个五角星、30个正方形和12个正五边形组成[1]，每个顶点都是每个顶点都是五边形、正方形、五角星和另外一个正方形的公共顶点[8]。


面在顶点周围的分布

分类

[编辑]

由于斜方截半大十二面体的顶点图为梯形且具备点可递的特性，同时，其存在自相交的面，因此斜方截半大十二面体是一种自相交拟拟正多面体（Self-Intersecting Quasi-Quasi-Regular Polyhedra）。自相交拟拟正多面体一共有12种[9]，除了小双三角十二面截半二十面体外，其馀由阿尔伯特·巴杜罗（Albert Badoureau）于1881年发现并描述。[10]

自相交拟拟正多面体
（Self-Intersecting Quasi-Quasi-Regular Polyhedra）

小立方立方八面体
大立方截半立方体
非凸大斜方截半立方体
小十二面截半二十面体

大十二面截半二十面体
小双三角十二面截半二十面体
大双三角十二面截半二十面体
二十面化截半大十二面体

小二十面化截半二十面体
大二十面化截半二十面体
斜方截半大十二面体
非凸大斜方截半二十面体

相关多面体

[编辑]

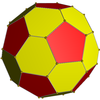有数种均匀多面体与均匀多面体复合体和斜方截半大十二面体共用顶点排布，分别为十复合三角柱（英语：compound of ten triangular prisms）、二十复合三角柱（英语：compound of ten triangular prisms）和斜方二十面体等。


凸包
斜方截半大十二面体
二十面化截半大十二面体

斜方二十面体
十复合三角柱（英语：compound of ten triangular prisms）
二十复合三角柱（英语：compound of ten triangular prisms）

倒角大十二面体

[编辑]

斜方截半大十二面体可以由小星形十二面体透过离面（Cantellation）变换而成[注 1]，也可以由大十二面体透过离面（Cantellation）变换而成，其变换过程也可以视为先倒角再截去顶点而得[11]，因此倒角大十二面体可以视为斜方截半大十二面体截角变换的原像。


倒角大二十面体
截角的倒角大二十面体
倒角大二十面体的面
青蓝色为三角形面
绿色为六边形面
倒角大二十面体的面
在顶点周围的排布

参见

[编辑]

注释

[编辑]
  1. ^ 1.0 1.1 斜方截半大十二面体的施莱夫利符号可以计为rr{5/2,5}[2]，其中{5/2,5}为小星形十二面体的施莱夫利符号表示方式[3]，而rr表示离面（Cantellation）变换[4]

参考文献

[编辑]
  1. ^ 1.0 1.1 1.2 Raded-Facetings. polyedergarten.de. [2019-10-14]. （原始内容存档于2018-09-17）. 
  2. ^ 2.0 2.1 Weisstein, Eric W. (编). Uniform Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  3. ^ Weisstein, Eric W. (编). Small Stellated Dodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  4. ^ 4.0 4.1 Grabowiecka, Zofia, The decoration of a Coxeter—Dynkin diagram and the Schläfli symbol as two methods to describe polytopes generated by finite reflection groups., Journal of Physics: Conference Series 1194 (1) (IOP Publishing), 2019, 1194 (1): 012039 
  5. ^ Wenninger, Magnus（英语：Magnus J. Wenninger）. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9. 
  6. ^ 6.0 6.1 38: rhombidodecadodecahedron. mathconsult.ch. [2019-10-14]. （原始内容存档于2018-05-02）. 
  7. ^ N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  8. ^ George W. Hart. Uniform Polyhedra. [2019-10-14]. （原始内容存档于2018-10-31）. 
  9. ^ David I. McCooey. Self-Intersecting Quasi-Quasi-Regular Polyhedra. [2022-08-07]. （原始内容存档于2022-08-22）. 
  10. ^ Jean Paul Albert Badoureau. Mémoire sur les Figures Isocèles. Journal de l'École polytechnique. 1881, (49): 47–172. 
  11. ^ Robert FERRÉOL. RHOMBIDODÉCADODÉCAÈDRE, RHOMBICOSAÈDRE et ICOSIDODÉCADODÉCAÈDRE. mathcurve.com. 2008 [2019-10-14]. （原始内容存档于2017-04-01） （法语）. 
检索自“https://zh.wikipedia.org/w/index.php?title=斜方截半大十二面體&oldid=75633558”