阿基米德立体
阿基米德立体是一种高度对称的半正多面体，且使用两种或以上的正多边形为面的凸多面体（不包括棱柱及反棱柱），并且都是可以从正多面体经过截角、截半、截边等操作构造。阿基米德立体的每个顶点的情况相同，共有13种。阿基米德曾研究半正多面体（虽然其研究纪录已佚），故有人将半正多面体唤作阿基米德立体。因为面是由正多边形组成的，每个相邻的正多边形的边长相等，故阿基米德立体的边均有相同长度。阿基米德立体的对偶多面体是卡塔兰立体。
半正多面体一词不只是指13种阿基米德立体，而是指所有具有对称群且由2种或2种以上正多边形所组成的多面体[1][2]。
截半多面体(阿基米德立体)
[编辑]在柏拉图立体中，从一条棱斩去另一条棱的中点所得出的多面体。这两种多面体又合称为拟正多面体。
| 名称 (顶点布局) |
透视图 | 旋转透视图 | 立体图 | 展开图 | 面 | 边 | 顶点 | 所属点群 | |
|---|---|---|---|---|---|---|---|---|---|
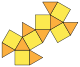
| 截半立方体 (截半八面体) (3.4.3.4) |
|
|
|
|
14 | 三角形×8 正方形×6 |
24 | 12 | Oh群 |
| 截半二十面体 (截半十二面体) (三十二面体) (3.5.3.5) |
|
|
|
|
32 | 三角形×20 五边形×12 |
60 | 30 | Ih群 |
截角多面体
[编辑]| 名称 (顶点布局) |
透视图 | 旋转透视图 | 立体图 | 展开图 | 面 | 边 | 顶点 | 所属点群 | |
|---|---|---|---|---|---|---|---|---|---|
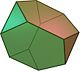
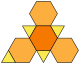
| 截角四面体 (3.6.6) |
|
|
|
|
8 | 三角形×4 六边形×4 |
18 | 12 | Td群 |
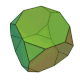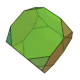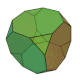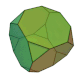
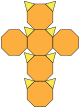
| 截角立方体 (3.8.8) |
|
|
|
|
14 | 三角形×8 八边形×6 |
36 | 24 | Oh群 |
| 截角八面体 (4.6.6) |
|
|
|
|
14 | 正方形×6 六边形×8 |
36 | 24 | Oh群 |
| 小斜方截半立方体 (3.4.4.4 ) |
|
|
|
|
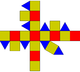
26 | 三角形×8 正方形×18 |
48 | 24 | Oh群 |
| 大斜方截半立方体 (4.6.8) |
|
|
|
|
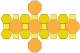
26 | 正方形×12 六边形×8 八边形×6 |
72 | 48 | Oh群 |
| 扭棱立方体 (3.3.3.3.4) (具有两种手性镜像) |
 
|
 
|
|
|
38 | 三角形×32 正方形×6 |
60 | 24 | O群 |
| 截角十二面体 (3.10.10) |
|
|
|
|
32 | 三角形×20 十边形×12 |
90 | 60 | Ih群 |
| 截角二十面体(足球的形状) (5.6.6) |
|
|
|
|
32 | 五边形×12 六边形×20 |
90 | 60 | Ih群 |
| 小斜方截半二十面体 (小斜方三十二面体) (3.4.5.4) |
|
|
|
|
62 | 三角形×20 正方形×30 五边形×12 |
120 | 60 | Ih群 |
| 大斜方截半二十面体 (大截角截半二十面体) (大斜方三十二面体) (大截角三十二面体) (4.6.10) |
|
|
|
|
62 | 正方形×30 六边形×20 十边形×12 |
180 | 120 | Ih群 |
| 扭棱十二面体 (3.3.3.3.5) (具有两种手性镜像) |
 
|
 
|
|
|
92 | 三角形×80 五边形×12 |
150 | 60 | I群 |
参考文献
[编辑]- ^ 《图解数学辞典》天下远见出版 ISBN 986-417-614-5
- ^ Illustrated Dictionary of Maths 2003 Usborne Publishing Ltd.
星号*表示该立体属于阿基米德立体。 黄色和红色为来自原像的面；蓝色为截边出现的正方形面；灰色为扭棱出现的三角形面。 |
