在數學 和計算機科學 中,歐拉方法 (英語:Euler method [註 1] 數值 方法,用以對給定初值的常微分方程 [註 2]
歐拉方法是常微分方程數值方法 顯式方法 ;也是一個一階 方法,意味著其局部截斷誤差[註 3] 正比於 步長的平方,並且其全局截斷誤差正比於步長。[註 4]
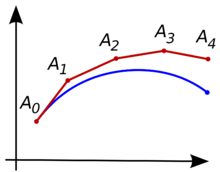
歐拉方法的圖示。待求的曲線為藍色,它的折線近似為紅色。 考慮計算這樣的一個未知曲線的形狀:它具有給定的起點並且滿足一個給定的微分方程。 這裡,所謂「微分方程」可以看作能夠通過曲線上任意點的位置而計算出這一點的切線 斜率 的公式。
思路是,一開始只知道曲線的起點(假設為
A
0
{\displaystyle A_{0}}
A
0
{\displaystyle A_{0}}
順著切線向前走一小步到點
A
1
{\displaystyle A_{1}}
A
1
{\displaystyle A_{1}}
折線
A
0
A
1
A
2
A
3
…
{\displaystyle A_{0}A_{1}A_{2}A_{3}\dots }
圖示為方程
y
′
=
y
,
y
(
0
)
=
1
{\displaystyle y'=y,y(0)=1}
中點法
y
=
e
t
{\displaystyle y=e^{t}}
h
=
1.0
{\displaystyle h=1.0}
圖示為同一個方程在步長
h
=
0.25
{\displaystyle h=0.25}
以以下微分方程為例
y
′
(
t
)
=
f
(
t
,
y
(
t
)
)
,
y
(
t
0
)
=
y
0
,
{\displaystyle y'(t)=f(t,y(t)),\qquad y(t_{0})=y_{0},}
希望用 y 在點 (t0 ,y(t0 )) 附近的線性近似來得到其近似解(也就是 y 的泰勒展開式 的前二項)。利用時間 t n 時的數值,若用單步的歐拉方法,可得到時間 t n+1 = t n + h 時的近似值如下:
y
n
+
1
=
y
n
+
h
f
(
t
n
,
y
n
)
.
{\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).\qquad \qquad }
歐拉方法是一種顯型方法,也就是說
y
n
+
1
{\displaystyle y_{n+1}}
y
i
{\displaystyle y_{i}}
i
≤
n
{\displaystyle i\leq n}
歐拉方法可以求解一階的微分方程,而任何
N
{\displaystyle N}
對於微分方程
y
(
N
)
(
t
)
=
f
(
t
,
y
(
t
)
,
y
′
(
t
)
,
…
,
y
(
N
−
1
)
(
t
)
)
{\displaystyle y^{(N)}(t)=f(t,y(t),y'(t),\ldots ,y^{(N-1)}(t))}
可以通過新設輔助變量
z
1
(
t
)
=
y
(
t
)
,
z
2
(
t
)
=
y
′
(
t
)
,
…
,
z
N
(
t
)
=
y
(
N
−
1
)
(
t
)
{\displaystyle z_{1}(t)=y(t),z_{2}(t)=y'(t),\ldots ,z_{N}(t)=y^{(N-1)}(t)}
z
′
(
t
)
=
(
z
1
′
(
t
)
⋮
z
N
−
1
′
(
t
)
z
N
′
(
t
)
)
=
(
y
′
(
t
)
⋮
y
(
N
−
1
)
(
t
)
y
(
N
)
(
t
)
)
=
(
z
2
(
t
)
⋮
z
N
(
t
)
f
(
t
,
z
1
(
t
)
,
…
,
z
N
(
t
)
)
)
{\displaystyle \mathbf {z} '(t)={\begin{pmatrix}z_{1}'(t)\\\vdots \\z_{N-1}'(t)\\z_{N}'(t)\end{pmatrix}}={\begin{pmatrix}y'(t)\\\vdots \\y^{(N-1)}(t)\\y^{(N)}(t)\end{pmatrix}}={\begin{pmatrix}z_{2}(t)\\\vdots \\z_{N}(t)\\f(t,z_{1}(t),\ldots ,z_{N}(t))\end{pmatrix}}}
這是一個以
z
(
t
)
{\displaystyle \mathbf {z} (t)}
[1]
設微分方程為
y
′
=
y
{\displaystyle y'=y}
y
(
0
)
=
1
{\displaystyle y(0)=1}
y
3
{\displaystyle y_{3}}
h
=
1
{\displaystyle h=1}
歐拉法為:
y
n
+
1
=
y
n
+
h
f
(
t
n
,
y
n
)
.
{\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).}
首先求
f
(
t
0
,
y
0
)
{\displaystyle f(t_{0},y_{0})}
n
=
0
{\displaystyle n=0}
f
{\displaystyle f}
f
(
t
,
y
)
=
y
{\displaystyle f(t,y)=y}
f
(
t
0
,
y
0
)
=
f
(
0
,
1
)
=
1.
{\displaystyle f(t_{0},y_{0})=f(0,1)=1.}
透過以上步驟,求得解曲線在點
(
0
,
1
)
{\displaystyle (0,1)}
y
{\displaystyle y}
t
{\displaystyle t}
Δ
y
/
Δ
t
{\displaystyle \Delta y/\Delta t}
接著是
h
⋅
f
(
y
0
)
=
1
⋅
1
=
1.
{\displaystyle h\cdot f(y_{0})=1\cdot 1=1.}
y
0
+
h
f
(
y
0
)
=
y
1
=
1
+
1
⋅
1
=
2.
{\displaystyle y_{0}+hf(y_{0})=y_{1}=1+1\cdot 1=2.}
重複以上步驟求出
y
2
{\displaystyle y_{2}}
y
3
{\displaystyle y_{3}}
y
2
=
y
1
+
h
f
(
y
1
)
=
2
+
1
⋅
2
=
4
{\displaystyle y_{2}=y_{1}+hf(y_{1})=2+1\cdot 2=4}
y
3
=
y
2
+
h
f
(
y
2
)
=
4
+
1
⋅
4
=
8
{\displaystyle y_{3}=y_{2}+hf(y_{2})=4+1\cdot 4=8}
由於歐拉法屬於遞歸算法,把運算整理成表格也許有助於避免計算錯誤。
y
n
{\displaystyle y_{n}}
t
n
{\displaystyle t_{n}}
y
′
(
t
)
{\displaystyle y'(t)}
h
{\displaystyle h}
d
y
{\displaystyle dy}
y
n
+
1
{\displaystyle y_{n+1}}
1
0
1
1
1
2
2
1
2
1
2
4
4
2
4
1
4
8
歐拉法的局部截尾誤差(Local truncation error, LTE)是指在實施一次歐拉法所產生的誤差,是指經過一步的數值解
y
1
{\displaystyle y_{1}}
t
1
=
t
0
+
h
{\displaystyle t_{1}=t_{0}+h}
y
1
{\displaystyle y_{1}}
y
1
=
y
0
+
h
f
(
t
0
,
y
0
)
.
{\displaystyle y_{1}=y_{0}+hf(t_{0},y_{0}).\quad }
對於精確解,使用泰勒級數展開給出:
y
(
t
0
+
h
)
=
y
(
t
0
)
+
h
y
′
(
t
0
)
+
1
2
h
2
y
″
(
t
0
)
+
O
(
h
3
)
.
{\displaystyle y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).}
歐拉法的局部截尾誤差為:
L
T
E
=
y
(
t
0
+
h
)
−
y
1
=
1
2
h
2
y
″
(
t
0
)
+
O
(
h
3
)
.
{\displaystyle \mathrm {LTE} =y(t_{0}+h)-y_{1}={\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).}
當
y
{\displaystyle y}
[2]
結果顯示:當步長
h
{\displaystyle h}
h
2
{\displaystyle h^{2}}
龍格-庫塔法 和線性多步法
h
p
{\displaystyle h^{p}}
p >2)成比例。
全局截尾誤差(Global truncation error, GTE)是指在一個固定時間
t
{\displaystyle t}
[3]
(
t
−
t
0
)
/
h
{\displaystyle (t-t_{0})/h}
h
2
{\displaystyle h^{2}}
h
{\displaystyle h}
[4]
這個直觀的推測可以被嚴謹地證明。如果解
y
{\displaystyle y}
f
{\displaystyle f}
y
{\displaystyle y}
利普希茨連續 的,那麼全局截尾誤差是有界的:
|
GTE
|
≤
h
M
2
L
(
e
L
(
t
−
t
0
)
−
1
)
{\displaystyle |{\text{GTE}}|\leq {\frac {hM}{2L}}(e^{L(t-t_{0})}-1)\qquad \qquad }
其中
M
{\displaystyle M}
y
{\displaystyle y}
L
{\displaystyle L}
f
{\displaystyle f}
[5]
這種精確的形式其實是沒有什麼意義的,通常情況下這個上界都會嚴重高估了歐拉法所造成的實際誤差。[6]
h
{\displaystyle h}
[7]
Atkinson, Kendall A., An Introduction to Numerical Analysis 2nd, New York: John Wiley & Sons , 1989, ISBN 978-0-471-50023-0 Ascher, Uri M.; Petzold, Linda R., Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, Philadelphia: Society for Industrial and Applied Mathematics, 1998, ISBN 978-0-89871-412-8 Butcher, John C., Numerical Methods for Ordinary Differential Equations, New York: John Wiley & Sons , 2003, ISBN 978-0-471-96758-3 Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard, Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag , 1993, ISBN 978-3-540-56670-0 Iserles, Arieh, A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press , 1996, ISBN 978-0-521-55655-2 Lakoba, Taras I., Simple Euler method and its modifications (PDF) (Lecture notes for MATH334, University of Vermont), 2012 [2016-01-02 ] , (原始內容存檔 (PDF) 於2012-07-12)