卡塔蘭立體

菱形十二面體

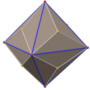
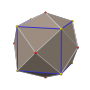
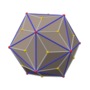
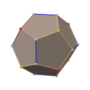
卡塔蘭立體是半正多面體的對偶多面體，都是凸多面體。1865年比利時數學家歐仁·查理·卡塔蘭最先描述它們。

卡塔蘭立體面可遞而點不可遞，而其對偶多面體半正多面體點可遞而面不可遞。只有兩個邊可遞的卡塔蘭立體：菱形十二面體和菱形三十面體。

所有多面體中只有13種是卡塔蘭立體，其對偶多面體均為阿基米德立體（半正多面體的子集）。

卡塔蘭立體列表

13個卡塔蘭立體的一個視角

另一個視角

名稱	圖像	展開圖	對偶	面	邊	頂點	頂點佈局	點群
三角化四面體	(動畫)		截角四面體	12	18	8	等腰三角形 V3.6.6	Td群
菱形十二面體	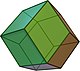(動畫)		截半立方體	12	24	14	菱形 V3.4.3.4	Oh群
三角化八面體	(動畫)		截角立方體	24	36	14	等腰三角形 V3.8.8	Oh群
四角化立方體	(動畫)		截角八面體	24	36	14	等腰三角形 V4.6.6	Oh群
鳶形二十四面體	(動畫)		小斜方截半立方體	24	48	26	鳶形 V3.4.4.4	Oh群
四角化菱形十二面體	(動畫)		大斜方截半立方體	48	72	26	不等邊三角形 V4.6.8	Oh群
五角二十四面體 (有兩種手性鏡像)	(動畫) (動畫)		扭稜立方體	24	60	38	不等邊五邊形 V3.3.3.3.4	O群
菱形三十面體	(動畫)		截半二十面體	30	60	32	菱形 V3.5.3.5	Ih群
三角化二十面體	(動畫)		截角十二面體	60	90	32	等腰三角形 V3.10.10	Ih群
五角化十二面體	(動畫)		截角二十面體	60	90	32	等腰三角形 V5.6.6	Ih群
鳶形六十面體	(動畫)		小斜方截半二十面體	60	120	62	鳶形 V3.4.5.4	Ih群
四角化菱形三十面體	(動畫)		大斜方截半二十面體	120	180	62	不等邊三角形 V4.6.10	Ih群
五角六十面體 (有兩種手性鏡像)	(動畫) (動畫)		扭稜十二面體	60	150	92	不等邊五邊形 V3.3.3.3.5	I群